در فرایند «تحلیل داده» (Data Analytics) پیش از هر چیزی ابتدا لازم است تا داده‌ها را پردازش کنید. به‌طور معمول، داده‌های خام قابل ارزیابی نیستند و از همین جهت، دو سوم زمان در تحلیل داده صرف فرایندهایی مانند «پاک‌سازی» (Data Cleaning) و تبدیل داده‌ها به فرمتی قابل استفاده می‌شود. امکان دارد در طول فرایند پاک‌سازی، با داده‌هایی بسیار متفاوت از دیگر نمونه‌ها یعنی «داده‌های پرت» (Outlier) مواجه شوید. در این مطلب از مجله فرادرس، یاد می‌گیریم داده پرت چیست و با نحوه تشخیص آن آشنا می‌شویم.

در این مطلب، ابتدا یاد می‌گیریم منظور از داده پرت چیست و به معرفی انواع مختلف آن می‌پردازیم. سپس از دلایل وجود مشکل داده پرت در دیتاست‌ها می‌گوییم و با نحوه تشخیص این گروه از داده‌ها آشنا می‌شویم. در انتهای این مطلب از مجله فرادرس، به چند مورد از روش‌های ترسیم داده پرت اشاره می‌کنیم و همچنین به تعدادی از سوالات متداول در این حوزه پاسخ می‌دهیم.

منظور از داده پرت چیست؟

به بیان ساده، داده پرت نمونه‌ایست که فاصله زیادی از نظر شباهت با نقاط داده همسایه خود در یک «مجموعه‌داده» (Dataset) دارد. به عنوان مثالی از جهان حقیقی، می‌توانیم به قد زرافه‌ها اشاره کنیم که به‌طور میانگین برابر با ۵ متر است. حالا اگر قد زرافه‌ای ۳ متر یا کمتر باشد، در مقایسه با سایر زرافه‌ها، نمونه داده‌ای پرت در نظر گرفته می‌شود. در صورتی که به مشکل داده‌های پرت رسیدگی نشود، امکان به‌وجود آمدن «ناهنجاری» (Anomaly) و ناهماهنگی در ارزیابی نهایی وجود دارد. به دو دلیل زیر، باید توجه ویژه‌ای به داده‌های گمشده داشته باشیم:

1. وجود داده‌های پرت ممکن است بر نتایج حاصل از تجزیه و تحلیل داده تاثیر منفی بگذارد.
2. احتمال دارد کشف و شناسایی داده‌های پرت یا رفتار این قبیل از داده‌ها، همان اطلاعاتی باشد که تحلیلگر داده برای ارزیابی به آن نیاز دارد.

حالا که یاد گرفتیم داده پرت چیست، در ادامه به شرح انواع مختلف این گروه از داده‌ها می‌پردازیم.

انواع مختلف داده پرت چیست؟

به‌طور کلی، می‌توان انواع داده‌های پرت را به دو دسته زیر تقسیم کرد:

• «داده‌های پرت تک متغیره» (Univariate Outliers): مقداری غیرعادی که تنها به یک متغیر نسبت داده می‌شود. به عنوان مثال، بلند قدترین انسان، قدی برابر با ۲ متر و ۵۱ سانتی‌متر دارد. داده پرتِ تک متغیره‌ای که تنها در معیار قد، غیرعادی محسوب می‌شود.
• «داده‌های پرت چند متغیره» (Multivariate Outliers): ترکیبی از مقادیر غیرعادی و نامعمول که به حداقل دو متغیر نسبت داده می‌شوند. به عنوان مثال، اگر دو معیار وزن و قد گروهی از بزرگ‌سالان را در نظر بگیرید، ممکن است نمونه‌ای را با وزن ۵۰ کیلوگرم و قد ۱۷۵ سانتی‌متر در مجموعه‌داده خود مشاهده کنید. با بررسی جداگانه هر کدام از معیارها، متوجه می‌شویم که هم وزن ۵۰ کیلوگرم عادی و هم قد برابر با ۱۷۵ سانتی‌متر معمول است. اما ترکیب این دو، یعنی فردی با این وزن و قد، در گروه داده‌های پرت چند متغیره قرار می‌گیرد.

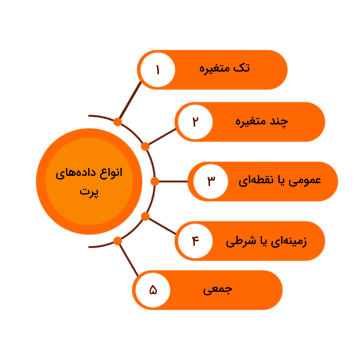
علاوه‌بر این دو معیار اصلی، ممکن است شاهد طبقه‌بندی‌های دیگری نیز برای انواع داده‌های پرت باشید؛ مانند:

• «داده‌های پرت عمومی یا نقطه‌ای» (Global Outliers | Point Outliers): تک نمونه داده‌ای که بسیار دورتر از توزیع کلی مجموعه‌داده جای می‌گیرد.
• «داده‌های پرت زمینه‌ای یا شرطی» (Contextual Outliers | Conditional Outliers): مقادیری که انحراف چشمگیری از سایر نقاط داده با موضوع مشابه دارند. یعنی ممکن است در صورت متفاوت بودن موضوع مسئله، چنین مقادیری در گروه داده‌های پرت قرار نگیرند. وجود داده‌های پرت زمینه‌ای در دیتاست‌های «سری زمانی» (Time Series) رایج است.
• «داده‌های پرت جمعی» (Collective Outliers): زیرمجموعه‌ای از نقاط داده که با سایر نمونه‌های دیتاست تفاوت عمده و اساسی دارند.

چگونه روش برخورد با داده های پرت را یاد بگیریم؟

وجود داده‌های پرت و نامتعارف در پروژه‌های کاربردی امری اجتناب ناپذیر است. داده‌هایی که مي‌توانند بر دقت و عملکرد مدل‌های یادگیری ماشین تاثیر منفی بگذارند. بنابراین، آشنایی با روش‌های صحیح برخورد با داده‌های پرت بسیار اهمیت داشته و پیش از هر چیز، باید درک مناسبی از ماهیت این گروه از داده‌ها به‌دست آورید. اگر قصد دارید به شیوه‌ای کارآمد این موضوع حیاتی را یاد بگیرید، مشاهده فیلم‌های آموزشی فرادرس را به ترتیبی که در زیر آورده شده است به شما پیشنهاد می‌کنیم:

دلیل وجود مشکل داده پرت در دیتاست ها چیست؟

حالا که به‌خوبی می‌دانیم داده پرت چیست، در این بخش به چرایی ایجاد مشکل داده پرت در دیتاست‌ها پاسخ می‌دهیم. در فهرست زیر به چند مورد از رایج‌ترین دلایل ایجاد مشکل داده پرت اشاره کرده‌ایم:

• خطای انسانی، مانند اشتباه تایپی هنگام وارد کردن دستی داده‌ها.
• خطاهای هدفمند، مانند زمانی که از قصد و به‌منظور اجرای تکنیک‌های آزمایشی، تعدادی داده پرت به مجموعه‌داده اضافه می‌شود.
• خطای نمونه‌برداری ناشی از استخراج داده‌ها از منابعی نامعتبر.
• خطاهایی که بعد از اجرای فرایند «پردازش داده» (Data Processing) و به‌دلیل تغییر داده‌ها ایجاد می‌شوند.
• خطاهای اندازه‌گیری که در نتیجه ارزیابی نادرست به‌وجود می‌آیند.
• خطاهای آزمایشی حاصل از مراحل اجرا، برنامه‌ریزی یا استخراج داده.
• گاهی نیز وجود داده‌های پرت طبیعی است و به هیچ‌کدام از خطاهای فوق ارتباطی ندارد. به این قبیل از خطاها، «بدیع» (Novelties) نیز گفته می‌شود.

چگونه داده های پرت را تشخیص دهیم؟

پس از آن‌که یاد گرفتیم داده پرت چیست و با انواع و همچنین دلایل ایجاد آن آشنا شدیم، در این بخش به معرفی راه‌های تشخیص داده‌های پرت در مجموعه‌داده می‌پردازیم. اگر مجموعه‌داده کوچک باشد، تشخیص داده پرت کار آسانی است. به عنوان مثال از میان داده‌های عددی ۲۸، ۲۶، ۲۱، ۲۴ و ۷۸، مشخص است که عدد ۷۸ نقش داده پرت را بازی می‌کند. اما هنگام کار با مجموعه‌داده‌های بزرگ یا «کلان داده» (Big Data)، تشخیص داده پرت به این راحتی نیست و باید از ابزارهای دیگری نیز استفاده کنیم. توجه داشته باشید که انتخاب روش مناسب، به نوع دیتاست و ابزارهایی که استفاده می‌کنید بستگی دارد.

از نظر آماری، داده‌ای پرت است که در یکی از دو شرط زیر صدق کند:

Outlier < Q1 - 1.5(IQR)
Or
Outlier > Q3 + 1.5(IQR)

در واقع داده‌ای پرت در نظر گرفته می‌شود که به اندازه ۱/۵ برابر «دامنه میان چارکی» (Interquartile Range | IQR) از چارک پایین (Q1) یا چارک بالا (Q3) فاصله داشته باشد. به‌ترتیب، داده‌های پرتی که در شرط اول و دوم صدق کنند را «داده پرت پایین» (Low Outlier) و «داده پرت بالا» (High Outlier) می‌نامند. همان‌طور که ملاحظه می‌کنید، پیش از تشخیص داده‌های پرت، ابتدا باید مقادیری همچون Q3، Q1 و IQR را محاسبه کنیم. از همین جهت و حالا که یاد گرفتیم داده پرت چیست، در ادامه این بخش از مطلب، با نحوه تشخیص داد‌های پرت در دیتاست‌هایی با تعداد نمونه زوج و فرد آشنا می‌شویم. برای آشنایی بیشتر با مفهوم چارک‌ها، مطالعه مطلب زیر را از مجله فرادرس به شما پیشنهاد می‌کنیم:

تشخیص داده پرت در دیتاست فرد

فرض کنید محتوای دیتاست یا مجموعه‌داده ما از قرار زیر است:

25, 14, 6, 5, 5, 30, 11, 11, 13, 4, 2

در اولین قدم، لازم است تا نمونه داده‌ها را به ترتیب صعودی و از کوچک به بزرگ مرتب کنیم:

2, 4, 5, 5, 6, 11, 11, 13, 14, 25, 30

کوچک‌ترین و بزرگ‌ترین مقادیر این دیتاست به‌ترتیب برابر با ۲ و ۳۰ هستند.

محاسبه میانه در دیتاست

در قدم بعدی باید معیار «میانه» (Median) را که با عنوان چارک دوم یا Q2 نیز شناخته می‌شود پیدا کنیم. اگر مانند دیتاست ما، تعداد نمونه‌ها فرد باشد، مقدار میانه برابر با تک نمونه داده‌ایست که در میانه مجموعه قرار دارد. حالا و از آنجا که ۱۱ نمونه داریم، راحت‌ترین راه، تقسیم مجموعه‌داده به دو بخش مساوی با ۵ مقدار است. به این صورت در هر طرف از مقدار میانه، ۵ عدد وجود دارد:

(2, 4, 5, 5, 6), 11, (11, 13, 14, 25, 30)

همان‌طور که ملاحظه می‌کنید، تنها یک نمونه است که بخش اول دیتاست را از بخش دوم آن جدا کرده است و در نتیجه، عدد ۱۱ همان مقدار میانه است. برای اطمینان از درستی پاسخ، می‌توان مانند زیر عمل کرد:

(total_number_of_samples + 1) / 2

با جایگذاری تعداد کل نمونه‌ها در عبارت بالا، به عدد ۶ می‌رسیم:

(11 + 1) / 2 = 6

نتیجه به‌دست آمده به این معنی است که نمونه ششم از مجموعه‌داده یا همان عدد ۱۱ برابر با مقدار میانگین (Q2) است.

محاسبه چارک پایین (Q1)

سپس برای یافتن چارک پایین، باید مقدار میانه نیمه اول که در سمت چپ دیتاست قرار دارد را پیدا کنیم. تا اینجا دیتاست ما به صورت زیر است:

(2, 4, 5, 5, 6), 11, (11, 13, 14, 25, 30)

نیمه اول یا پایینی دیتاست نیز شامل تعداد فردی از داده‌ها است. به‌طور دقیق‌تر، نیمه اول دیتاست ۵ نمونه دارد:

2, 4, 5, 5, 6

مانند قبل، این بخش از مجموعه‌داده را نیز به دو بخش مساوی با ۲ مقدار در هر طرف تقسیم کرده و نمونه‌ای که در میانه قرار دارد را انتخاب می‌کنیم:

(2, 4), 5, (5, 6)

بنابراین مقدار چارک پایین برابر با ۵ است. مجدد برای به‌دست آوردن جایگاه مقدار میانه این بخش از مجموعه‌داده مانند زیر عمل می‌کنیم:

(5 + 1) / 2 = 3

جایگاه سوم یا همان عدد ۵ برابر با چارک پایین (Q1) است.

محاسبه چارک بالا (Q3)

فرایند یافتن چارک بالا نیز مانند چارک پایین است. با این تفاوت که باید در نیمه دوم و سمت راست مجموعه‌داده به‌دنبال مقدار میانه باشیم:

11, 13, 14, 25, 30

دوباره این قسمت از دیتاست را به دو بخش مساوی تقسیم و نمونه سوم را به عنوان چارک بالا انتخاب می‌کنیم:

(11, 13), 14, (25, 30)

در نتیجه، عدد ۱۴ همان چارک بالا (Q3) است.

محاسبه دامنه میان چارکی (IQR)

به فاصله یا تفاضل میان چارک پایین (Q1) و چارک بالا (Q3)، دامنه میان چارکی گفته می‌شود:

IQR = Q3 - Q1

پس از آن‌که در مراحل قبلی، چارک پایین و بالا را به‌دست آوردیم، حالا می‌توانیم مقدار دامنه میان چارکی را نیز محاسبه کنیم:

IQR= 14 - 5
IQR = 9

مقدار دامنه میان چارکی (IQR) برابر با ۹ است.

پیدا کردن داده پرت

تا اینجا می‌دانیم که دیتاست ما از مقادیر زیر تشکل شده است:

2, 4, 5, 5, 6, 11, 11, 13, 14, 25, 30

همچنین پنج مقدار کوچک‌ترین عدد، چارک پایین، میانه، چارک بالا و بزرگ‌ترین عدد را نیز محاسبه کرده‌ایم:

MIN = 2
Q1 = 5
MED = 11
Q3 = 14
MAX = 30

در نهایت می‌خواهیم داده‌های پرت را پیدا کنیم. به‌خاطر دارید که داده پرت باید در یکی از دو شرط زیر صدق کند:

Outlier < Q1 - 1.5(IQR)
Or
Outlier > Q3 + 1.5(IQR)

برای پیدا کردن کوچک‌ترین داده پرت باید شرط اول را محاسبه کنیم:

Outlier < Q1 - 1.5(IQR)
Outlier < 5 - 1.5(9)
Outlier < 5 - 13.5 
Outlier < -8.5

از آنجا که عددی کوچکتر از ۸/۵- در دیتاست قرار ندارد، نتیجه می‌گیریم که هیچ داده پرتی در سمت کمینه قرار ندارد. در مرحله بعد با محاسبه شرط دوم، حد آستانه بزرگ‌ترین داده پرت را به‌دست می‌آوریم:

Outlier > Q3  + 1.5(IQR)
Outlier > 14 + 1.5(9)
Outlier > 14 + 13.5
Outlier > 27.5

با بررسی مجدد دیتاست، متوجه وجود عددی بیشتر از ۲۷/۵ می‌شویم:

2, 4, 5, 5, 6, 11, 11, 13, 14, 25, 30

در نتیجه، عدد ۳۰ برابر با بزرگ‌ترین داده پرت دیتاست ما است.

تشخیص داده پرت در دیتاست زوج

تشخیص مقادیری همچون Q2، Q1 و Q3 در دیتاست‌هایی با تعداد داده زوج، کمی متفاوت از دیتاست‌های فرد است. در ادامه با مراحل تشخیص داده پرت در دیتاست‌های زوج آشنا می‌شویم. برای یادگیری بیشتر در مورد مفاهیم آماری می‌توانید فیلم آموزشی مفاهیم آماری در داده کاوی فرادرس که لینک آن در ادامه آورده شده است را مشاهده کنید:

محاسبه میانه در دیتاست

فرض کنید دیتاستی با تعداد ۸ نمونه مانند زیر داریم:

10, 15, 20, 26, 28, 30, 35, 40

ترتیب داده‌ها در این دیتاست صعودی و از کوچک به بزرگ است و نیازی به مرتب‌سازی ندارد. برای یافتن مقدار میانه در دیتاست‌های زوج، باید مقدار بین دو عدد میانی مجموعه را پیدا کنیم. در نتیجه، دو عدد ۲۶ و ۲۸ را با یک‌دیگر جمع کرده و نتیجه را بر دو تقسیم می‌کنیم:

26 + 28 = 54
54 / 2 = 27

با توجه به محاسبات انجام شده، مقدار میانه (Q2) برابر با ۲۷ است.

محاسبه چارک پایین (Q1)

متفاوت با دیتاست‌های فرد که هنگام محاسبه دو چارک پایین و بالا، مقدار میانه را جدا در نظر می‌گرفتیم، در دیتاست‌هایی با تعداد نمونه زوج، تمامی داده‌ها را حفظ و مانند زیر، دیتاست را به دو قسمت تقسیم می‌کنیم:

10, 15, 20, 26 | 28, 30, 35, 40

با تکرار این فرایند، نیمه اول مجموعه‌داده را نیز به دو قسمت تقسیم می‌کنیم:

10, 15 | 20, 26

در نهایت و برای پیدا کردن مقدار چارک پایین، دو عددی که در میانه قرار دارند، یعنی ۱۵ و ۲۰ را با یک‌دیگر جمع و نتیجه را بر دو تقسیم می‌کنیم:

Q1 = (15 + 20) / 2
Q1 =  35 / 2
Q1 = 17.5

مقدار چارک پایین (Q1) برابر با ۱۷/۵ است.

محاسبه چارک بالا (Q3)

برای یافتن چارک بالا، باید بر نیمه دوم دیتاست متمرکز شده و آن را به دو قسمت تقسیم کنیم:

28, 30, 35, 40 -> 28, 30 | 35, 40

دو عدد ۳۰ و ۳۵ در میانه مجموعه قرار دارند. در نتیجه برای محاسبه مقدار میانه یا چارک بالا، این دو عدد را با یک‌دیگر جمع و تقسیم بر دو می‌کنیم:

Q3 = (30 + 35) / 2
Q3 = 65 / 2
Q3 = 32.5

همان‌طور که ملاحظه می‌کنید، مقدار چارک بالا (Q3) برابر با عدد ۳۲/۵ است.

محاسبه دامنه میان چارکی (IQR)

فرمول محاسبه دامنه میان چارکی در دیتاست‌های زوج همانند پیش بوده تفاوتی با دیتاست‌های فرد ندارد:

IQR = Q3 - Q1
IQR = 32.5 - 17.5
IQR = 15

عدد ۱۵ نشانگر دامنه میان چارکی (IQR) است.

پیدا کردن داده پرت

تا اینجا، مقدار پنج معیار کمترین نمونه، چارک پایین، میانه، چارک بالا و بیشترین نمونه به‌دست آمده است:

MIN = 10
Q1 = 17,5
MED = 27
Q3 = 32,5
MAX = 40

برای تشخیص داده‌های پرت در دیتاست باید از دو شرط زیر استفاده کنیم:

Outlier < Q1 - 1.5(IQR)
Or
Outlier > Q3 + 1.5(IQR)

ابتدا با جایگذاری مقادیر Q1 و IQR در شرط اول، مقدار کوچک‌ترین داده پرت را به‌دست می‌آوریم:

Outlier < 17.5 - 1.5(15)
Outlier < 17.5 - 22.5
Outlier < -5

از آنجا که نمونه داده‌ای کمتر از ۵- وجود ندارد، می‌توانیم نتیجه بگیریم که داده پرتی با مقدار کمینه نداریم. در نهایت برای پیدا کردن بزرگ‌ترین داده‌های پرت، مقادیر مورد نیاز را در شرط دوم جایگزین می‌کنیم:

Outlier > 32.5 + 1.5(15)
Outlier > 32.5 + 22.5
Outlier > 55

در میان تمام داده‌ها، هیچ نمونه‌ای نیست که مقداری بیش از ۵۵ داشته باشد. به همین خاطر، نتیجه می‌گیریم که داده پرتی با مقدار بیشینه وجود نداشته و در کل، دیتاست ما فاقد داده پرت است.

روش های ترسیم داده پرت

متخصصان تحلیل داده از تکنیک‌های «مصورسازی» (Visualization) برای ارائه نتایج حاصل شده به‌شیوه‌ای تعاملی و قابل درک استفاده می‌کنند. تکنیک‌هایی که نشان‌دهنده جریان‌های محبوب، الگوها و داده‌های پرت موجود در مجموعه‌داده‌های بزرگی مانند نقشه‌ها و نمودارها هستند. پس از آن‌که به پرسش داده پرت چیست پاسخ دادیم و نحوه تشخیص این قبیل از داده‌ها را نیز یاد گرفتیم، در این بخش به شرح دو مورد از کاربردی‌ترین روش‌های مصورسازی می‌پردازیم.

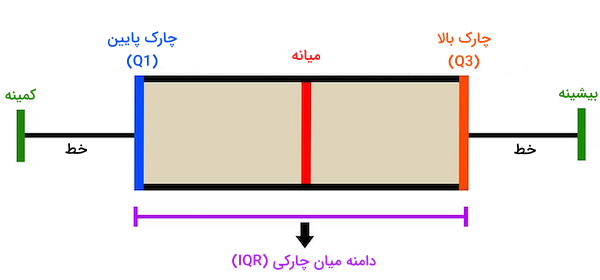
نمودار جعبه ای

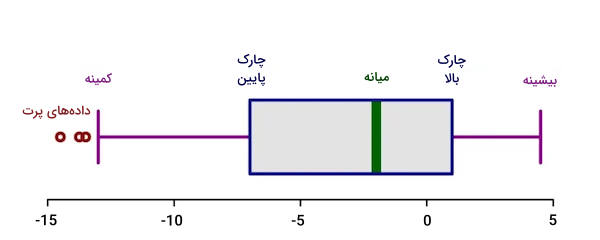
با ترسیم داده‌ها در قالب «نمودار جعبه‌ای» (Box Plot)، به‌راحتی می‌توانیم داده‌های پرت را تشخیص دهیم. منظور از جعبه در این نوع از نمودار، همان دامنه میان چارکی است که از «چارک» (Quartile) پایین تا چارک بالا ادامه داشته و در میانه آن نیز مقدار میانه یا همان Median قرار دارد. در دو طرف جعبه «خطوطی» (Whiskers) وجود دارند که بیانگیر مقادیر کمینه و بیشینه موجود در دیتاست هستند. اگر نمونه داده‌ای فرای این دو خط قرار بگیرد، از آن به عنوان داده پرت یاد می‌شود. هر چه جعبه به مقدار بیشینه نزدیک‌تر باشد، داده‌های پرت بیشتری در سمت کمینه قرار می‌گیرند. همچنین اگر جعبه در سمت مقدار کمینه قرار داشته باشد، اغلب داده‌های پرت شامل مقداری بیشینه خواهند بود. توجه داشته باشید که ابتدای جعبه چارک پایین یا Q1 و انتهای آن چارک بالا یا Q3 نام دارد.

نمودار نقطه ای

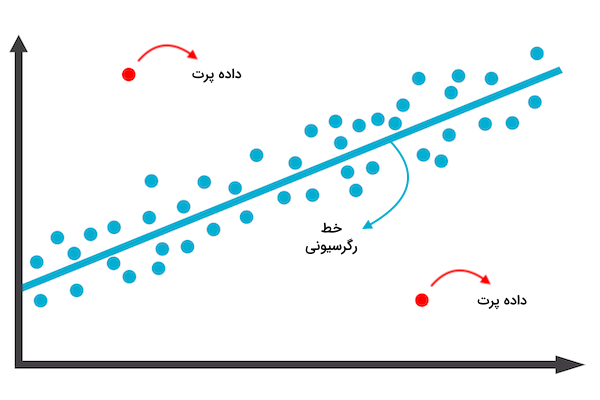
همان‌طور که از نام آن پیدا است، در «نمودار پراکندگی» (Scatter Plot) داده‌های دیتاست بر روی محوری با دو متغیر پراکنده می‌شوند. در این نمودار، داده‌های پرت همان نمونه‌هایی هستند که با فاصله دوری از خط «رگرسیونی» (Regression) یا همان خطی که داده‌ها نسبت به آن برازش شده‌اند قرار دارند.

مسیر یادگیری داده کاوی با فرادرس

اگر تا اینجا همراه مطلب بوده باشید، به‌خوبی می‌دانید که درک و تشخیص داده‌های پرت، تنها بخشی از فرایند پردازش داده است و در ادامه لازم است تا از نتایج به‌دست آمده در کاربردهای جامع‌تری مانند داده کاوی و یادگیری ماشین استفاده کنید. از همین جهت، شما به یک مسیر یادگیری نیاز دارید و فرادرس مجموعه‌ای از فیلم‌های آموزشی را فراهم کرده است که می‌توانید از طریق لینک زیر آن‌ها را مشاهده کنید:

سوالات متداول

حالا که می‌دانیم داده پرت چیست و با روش‌های تشخیص و همچنین مصورسازی آن آشنا شدیم، در این بخش به چند مورد از سوالات متداول در این زمینه پاسخ می‌دهیم.

منظور از داده پرت در مجموعه داده چیست؟

وقتی می‌گوییم داده‌ای پرت است، یعنی تفاوت زیادی با سایر نمونه داده‌ها دارد. به عنوان مثال، در کلاسی که دانش‌آموزان به ترتیب نمرات ۱۹، ۱۸، ۱۹، ۱۷ و ۵ را کسب کرده باشند، دانش‌آموز آخر با نمره ۵، از الگوی اصلی سایر نمرات فاصله داشته و در واقع همان داده پرت است.

نحوه تفسیر داده های پرت در علم آمار به چه صورت است؟

داده‌های پرت در گروه نمونه‌های بی‌کیفیت قرار می‌گیرند. با این حال، گاهی نشان‌دهنده شرایط ویژه‌ای مانند خطای انسانی، گزارش‌های نادرست و نمونه‌برداری ضعیف هستند.

چگونه داده های پرت را پیدا کنیم؟

برای ترسیم داده‌های پرت از روش‌های مصورسازی مانند نمودار جعبه‌ای و پراکندگی استفاده می‌شود و همچنین با محاسبه معیارهای آماری مانند دامنه میان چارکی (IQR)، به راحتی می‌توانیم داده‌های پرت را پیدا کنیم.

داده پرت چگونه تعریف می شود؟

از داده‌های پرت به عنوان ناهنجاری در مجموعه‌داده یاد می‌شود. به‌طور معمول، هر مقداری که فاصله زیادی از نظر شباهتی با سایر داده‌ها داشته باشد، نوعی داده پرت در نظر گرفته می‌شود.

جمع‌بندی

مدیریت داده‌های پرت فرایند جالب و گاهی پیچیده است که در کنار چالش‌برانگیز بودن، می‌تواند اطلاعات مفید و فراموش شده‌ای را در اختیار ما قرار دهد. در این مطلب از مجله فرادرس یاد گرفتیم داده پرت چیست و نحوه تشخیص این گروه از داده‌ها چگونه است. با این حال، در نهایت تصمیم‌گیری برای چگونگی مدیریت داده‌های پرت به نوع داده‌ها و اهداف مسئله بستگی دارد. پژوهشگران این حوزه با دانش و درک عمیقی که از منشاء داده‌های پرت به‌دست می‌آورند، نحوه برخورد مناسب با این داده‌ها را شناسایی کرده و به نتایج دقیق و قابل اعتمادی دست پیدا می‌کنند.