هنگامیکه میگوییم جسمی در حال حرکت است یا در نقطهای مشخص، بدون حرکت قرار دارد، منظورمان نسبت به نقطهای معین است که به عنوان نقطه مرجع شناخته میشود. حرکت، بدون انتخاب نقطهای به نام نقطه مرجع، معنایی ندارد. حرکت اجسام توسط عبارتهایی مانند تندی، سرعت، فاصله، جابجایی و شتاب، توصیف میشود. در فیزیک، دو نوع حرکت داریم: حرکت یکنواخت و حرکت غیریکنواخت. در حرکت یکنواخت، جسم با سرعت ثابت روی خطی مستقیم حرکت میکند. در این مطلب از مجله فرادرس، ابتدا به پرسش حرکت یکنواخت چیست به زبان ساده پاسخ میدهیم.
پس از تعریف حرکت یکنواخت به زبان ساده، فرمولهای استفاده شده در این حرکت را با حل مثالهای متفاوت، بررسی میکنیم. در ادامه، حرکت یکنواخت در مسیر مستقیم و غیرمستقیم را توضیح میدهیم. در پایان، تفاوت حرکت یکنواخت و غیریکنواخت را با یکدیگر بررسی و مثالهایی را در این مورد حل میکنیم.
حرکت یکنواخت چیست؟
به حرکتی که در آن جسم با سرعت ثابت روی خطی مستقیم حرکت میکند، حرکت یکنواخت گفته میشود. این بدان معنا است که سرعت جسم ثابت باقی میماند و جسم در بازههای زمانی داده شده، مسافت یکسانی را طی میکند. توجه به این نکته مهم است که در حرکت یکنواخت با سرعت ثابت، شتاب حرکت برابر صفر و در نتیجه، سرعت متوسط و سرعت لحظهای با یکدیگر برابر هستند. برای یادگیری بیشتر در مورد حرکت یکنواخت میتوانید فیلم آموزش فیزیک – پایه دوازدهم فرادرس که لینک آن در ادامه آورده شده است را مشاهده کنید.
برای آشنایی با حرکت یکنواخت و حل مسائل مربوط به آن باید با مفاهیمی مانند جابجایی، مسافت، سرعت، تندی و شتاب آشنا باشیم. در ادامه، این مفاهیم را به اختصار تعریف میکنیم و فرمول هریک از آنها در حرکت روی خط راست را بهدست میآوریم.
جابجایی چیست؟
جسم به هنگام حرکت روی خط راست میتواند روی مسیری افقی به چپ یا راست یا مسیری عمودی به سمت بالا یا پایین، حرکت کند. برای توصیف چنین حرکتی در فیزیک، باید نقطهای را به نام نقطه مرجع انتخاب کنیم. فرض کنید اتومبیلی از نقطه A، روی جادهای افقی شروع به حرکت کرده است. این نقطه را به عنوان نقطه مرجع انتخاب میکنیم. بنابراین، مکانهای سمت راست نقطه A مثبت و مکانهای سمت چپ این نقطه منفی خواهند بود.

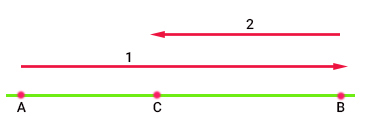
به هنگام حرکت اتومبیل روی خط مستقیم، مکان آن را در هر لحظه از زمان میتوانیم با بردار مکان نشان دهیم. ابتدای بردار مکان روی مبدا و انتهای آن روی مکان فعلی جسم قرار دارد. به عنوان مثال، اگر اتومبیل ۳ ثانیه پس از شروع حرکت به سمت راست، ۵ متر جابجا شده و به نقطه B رسیده باشد، بردار مکان، برداری به اندازه ۵ و در جهت راست، به صورت نشان داده شده در تصویر زیر است.

اگر اتومبیل در زمان $$t_1 $$ در مکان $$x(t_{1})$$ و در زمان $$t_2 $$ در مکان $$x(t_{2})$$ قرار داشته باشد، جابجایی آن در فاصله زمانی $$[t_{1}, t_{2}]$$ برابر $$x(t_{2})-x(t_{1})$$ خواهد بود. در واقع، مکان اتومبیل برابر تغییرات جابجایی آن از مبدا است. مکان و جابجایی کمیتهای برداری هستند و بزرگی و جهت دارند. علامت بردار نشاندهنده جهت بردار و قدر مطلق آن بیانگر بزرگی بردار است. همچنین، به این نکته توجه داشته باشید که جابجایی اتومبیل به مسیر طی شده توسط آن بستگی ندارد، بلکه به نقطهای ابتدایی و انتهایی وابسته است.
نکته: به هنگام حل مسائل مربوط به جابجایی، جهتی را به عنوان جهت مثبت انتخاب میکنیم. اگر جهت حرکت اتومبیل و جهت مثبت انتخاب شده، یکسان باشند، بردار جابجایی برداری مثبت است. اما اگر اتومبیل در خلاف جهت مثبت حرکت کند، بردار جابجایی به عنوان برداری منفی در نظر گرفته میشود.
مسافت چیست ؟
به کل مسیر پیموده شده توسط جسم، مسافت گفته میشود. در تصویر نشان داده شده در ادامه، فاصله A تا B برابر ۲۰ کیلومتر، فاصله A تا C برابر ۶ کیلومتر و فاصله C تا B برابر ۱۴ کیلومتر است. اگر اتومبیل از A به B و سپس به نقطه C حرکت کند، جابجایی آن برابر ۶ کیلومتر، اما مسافت طی شده توسط آن برابر ۳۴ کیلومتر است.
سرعت و تندی چیست ؟
به تغییرات مسافت با زمان تندی میگویند. سرعت نیز به صورت تغییرات جابجایی بر حسب زمان تعریف میشود. به این نکته توجه داشته باشید که تندی کمیتی اسکالر و سرعت کمیتی برداری است. این بدان معنا است که تندی فقط اندازه دارد، اما برای سرعت، علاوه بر اندازه، جهت را نیز در نظر میگیریم.
تفاوت حرکت غیریکنواخت و یکنواخت چیست؟
در بخش قبل فهمیدیم حرکت یکنواخت چیست. در حرکت یکنواخت، سرعت جسم ثابت باقی میماند و جسم در بازههای زمانی داده شده، مسافت یکسانی را طی میکند. حرکت اجسام در فیزیک گاهی یکنواخت و گاهی غیر یکنواخت است. سوال مهمی که ممکن است برای شما مطرح شود آن است که حرکت یکنواخت چه تفاوتی با حرکت غیریکنواخت دارد. تفاوتهای این دو حرکت به صورت خلاصه در جدول زیر آورده شدهاند.
| حرکت یکنواخت | حرکت یکنواخت |
| حرکت یکنواخت، حرکتی است که جسم در بازههای زمانی برابر، مسافتهای یکسانی را طی میکند. | حرکت یکنواخت، حرکتی است که جسم در بازههای زمانی برابر، مسافتهای متفاوتی را طی میکند. |
| سرعت در سراسر حرکت، ثابت باقی میماند. | سرعت تغییر میکند. |
| تندی در سراسر حرکت، ثابت باقی میماند. | تندی تغییر میکند. |
| شتاب برابر صفر است. | مقدار شتاب مخالف صفر است. |
| جسم با تندی ثابت روی خط راست حرکت میکند. | سرعت جسم، جهت حرکت آن یا هردو تغییر میکنند. |
| مسافت طی شده توسط جسم به طور مستقیم با زمان لازم برای طی کردن آن مسافت متناسب است. | مسافت طی شده توسط جسم به طور مستقیم با زمان لازم برای طی کردن آن مسافت متناسب نیست. |
| نمودار مکان زمانِ حرکت یکنواخت خطی مستقیم با شیب ثابت است. | نمودار مکان زمان حرکت غیریکنواخت، خط مستقیم با شیب ثابت نیست. |
| هیچ نیرو یا عامل خارجی به جسم در حرکت یکنواخت وارد نمیشود. | به جسم در حرکت غیریکنواخت نیروهای خارجی مانند نیروی اصطکاک یا نیروی گرانش وارد میشوند. |
| پیشبینی و تحلیل این حرکت آسانتر است. | پیشبینی این حرکت به دلیل تغییر اندازه و جهت سرعت، نیاز به معادلات پیچیدهتری دارد. |
| با استفاده از فرمول $$x= x_o + vt $$ میتوان مسائل مربوط به حرکت یکنواخت را حل کرد. | معادلات حرکت یکنواخت با توجه با ثابت یا متغیر بودن شتاب حرکت، انواع متفاوتی دارند. بنابراین، در حل مسائل از فرمولهای متنوعی میتوان استفاده کرد. |
| با استفاده از حرکت یکنواخت میتوان برخی نظریههای ساده در فیزیک را تحلیل کرد. | برای توصیف جهان واقعی و پیچیدگیهای آن باید از حرکت غیریکنواخت استفاده کرد. |
| توصیف این حرکت نیاز به آشنایی با ریاضیات پیچیده ندارد. | ممکن است برای توصیف دقیق حرکت غیریکنواخت جسم به ریاضیات پیچیده نیاز باشد. |
| مثال حرکت یکنواخت: حرکت اتومبیلی با تندی ثابت در بزرگراه یا حرکت توپی روی سطحِ بدون اصطکاک. | مثال حرکت غیریکنواخت: ترمز اتومبیلی در خیابان پس از دیدن عابر پیاده یا حرکت در مسیر پر از پیچوخم. |
تا اینجا فهمیدیم حرکت یکنواخت چیست و چه تفاوتی با حرکت غیریکنواخت دارد. در ادامه، حرکت یکنواخت را به صورت تصویری، با بیان فرمولهای مربوط به آن توضیح میدهیم.
نمودار مکان زمان در حرکت یکنواخت چیست؟
در بخش قبل فهمیدیم حرکت یکنواخت چیست و با مفاهیمی مانند مسافت، جابجایی، تندی و سرعت آشنا شدیم. در حرکت یکنواخت، جسم با تندی و سرعت ثابت روی خط مستقیم حرکت میکند. این بدان معنا است که سرعت جسم ثابت باقی میماند و جسم در بازههای زمانی داده شده، مسافت یکسانی را طی خواهد کرد. به عنوان مثال، اگر اتومبیلی با سرعت ثابت ۱۰۰ کیلومتر بر ساعت در اتوبانی حرکت کند، حرکت آن یکنواخت است. در این حالت، راننده سرعت اتومبیل را کاهش یا افزایش نمیدهد. حرکت یکنواخت، حرکت بسیار سادهای است. برای یادگیری بیشتر در مورد نمودار مکان زمان در حرکت یکنواخت و رسم آن میتوانید فیلم آموزش فیزیک – پایه دوازدهم فرادرس حل تمرین که لینک آن در ادامه آورده شده است را مشاهده کنید. همچنین، مطلب «نمودار مکان زمان – توضیح به زبان ساده + حل مثال» از مجله فرادرس به شما اطلاعات کاملی از حل مسائل مربوط به نمودار مکان زمان میدهد.
به این نکته توجه داشته باشید که هیچ جسمی در زندگی واقعی نمیتواند برای مدت زمان زیادی با سرعت ثابت حرکت کند، زیرا در دنیای واقعی، حرکت جسم با عاملی به نام اصطکاک روبرو میشود. اصطکاک نیرویی است که در خلاف جهت حرکت اجسام بر آنها وارد میشود و سرعت حرکت آنها را کاهش میدهد. تعریف دیگری برای حرکت یکنواخت وجود دارد. شتاب حرکت جسم در حرکت یکنواخت برابر صفر است. شتاب چیست؟ به تغییرات سرعت نسبت به زمان، شتاب گفته میشود.
از آنجا که در حرکت یکنواخت، تغییرات سرعت برابر صفر است، مقدار شتاب نیز برابر صفر خواهد بود. با رسم نمودار مکان جسم نسبت به زمان نیز میتوانیم حرکت یکنواخت را توصیف کنیم. نمودار مکان زمان، نمودار مهمی است که از آن برای توصیف حرکتهای مختلف در فیزیک استفاده میکنیم. در این نمودار، مکان جسم نسبت به مبدا را در زمانهای مختلف نشان میدهیم. نمودار مکان زمان برای حرکت یکنواخت را با استفاده از مثالی ساده رسم میکنیم.

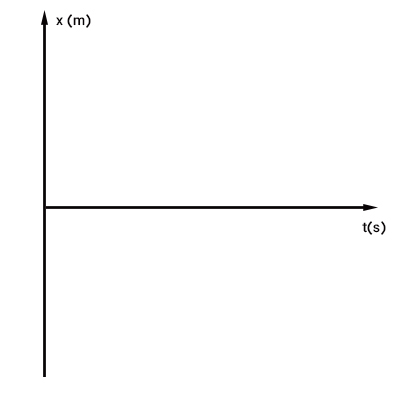
برای رسم این نمودار، ابتدا دو خط عمود بر یکدیگر را به صورت نشان داده شده در تصویر زیر رسم میکنیم. محور عمودی نشاندهنده مکان برحسب متر و محور افقی بیانگر زمان برحسب ثانیه است. به این نکته توجه داشته باشید که مکان جسم میتواند مقدارهای منفی داشته باشد، اما مقدار منفی برای زمان، بیمعنا است. از اینرو، دو محور عمود بر یکدیگر به گونهای رسم شدهاند که مکان بتواند مقدارهای منفی داشته باشد، اما زمان تنها مقدارهای مثبت را بپذیرد.
جسمی را در نظر بگیرید که در زمان صفر در مبدا مختصات قرار دارد. مکان این جسم نسبت به زمان، به صورت نشان داده شده در جدول زیر تغییر میکند.
| مکان جسم برحسب متر ($$x$$) | زمان برحسب ثانیه ($$t$$) |
| صفر | صفر |
| ۲ | ۱ |
| ۴ | ۲ |
| ۶ | ۳ |
| ۸ | ۴ |
برای رسم نمودار مکان زمان، مکان و زمانهای داده شده را به صورت نشان داده شده در تصویر زیر با نقطههای قرمزرنگ رسم میکنیم. با اتصال این نقطهها به یکدیگر، نمودار مکان زمان را رسم کردهایم.
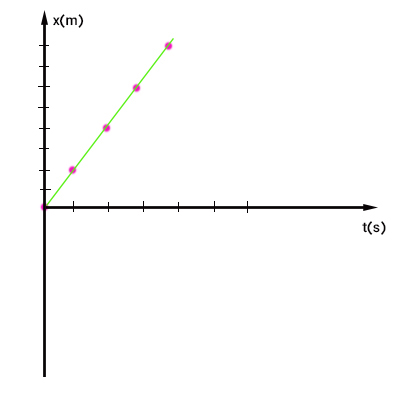
همانطور که در تصویر فوق مشاهده میکنید، نمودار مکان زمان جسم، خط مستقیم با شیبِ مثبت و ثابت است. به نمودار با دقت نگاه کنید. جسم در یک ثانیه اول حرکت (صفر تا یک ثانیه) چه مقدار جابجا شده است؟ جسم در زمان صفر، در مبدا مختصات و یک ثانیه بعد (ثانیه اول)، در دو متری مبدا مختصات قرار دارد. این بدان معنا است که جسم در دو ثانیه اول حرکت، دو متر جابجا شده است. جسم در یک ثانیه دوم حرکت (یک تا ۲ ثانیه) چه مقدار جابجا شده است؟
جسم در زمان یک ثانیه، در ۲ متری مبدا مختصات و یک ثانیه بعد (ثانیه دوم)، در ۴ متری مبدا مختصات قرار دارد. در نتیجه، جسم از زمان یک تا دو ثانیه، به اندازه ۲ متر دیگر جابجا شده است. آیا نکتهای توجه شما را به خود جلب کرده است؟ بله، جابجایی جسم در ثانیه اول، برابرِ جابجایی جسم در ثانیه دوم حرکت است. به بیان دیگر، جسم در هر ثانیه به اندازه دو متر جابجا و از مبدا دور شده است. در نتیجه، جسم در حرکت یکنواخت و در بازه زمانی مشابه، مسافت یکسانی را طی میکند.
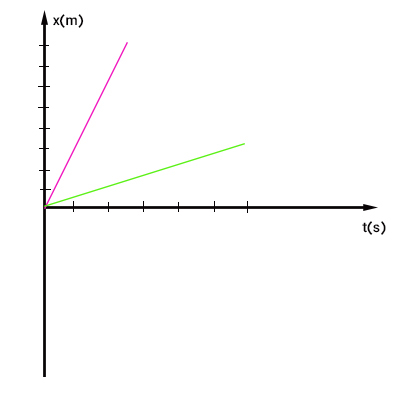
نمودار مکان زمان، خطی مستقیم با شیبی مشخص است. مقدار این شیب در حرکت یکنواخت با سرعت ثابت، عددی ثابت و یکسان است و با گذر زمان تغییر نمیکند. شاید از خود بپرسید شیب این خط چه کمیتی را نشان میدهد، سرعت. بنابراین، با محاسبه شیب خط نمودار مکان زمان، سرعت حرکت جسم را میتوانیم بهدست آوریم. هرچه شیب این خط بزرگتر باشد، جسم با سرعت بیشتری حرکت میکند. در مقابل، هرچه شیب خط کوچکتر باشد، جسم با سرعت کمتری حرکت خواهد کرد.
نمودار سرعت زمان در حرکت یکنواخت چیست؟
در بخش قبل فهمیدیم، نمودار مکان زمانِ حرکت یکنواخت، خطی مستقیم با شیبِ ثابت است. به تغییرات مکان نسبت به زمان، سرعت میگوییم:
$$overline{v}= frac { x _ 2 – x_ 1 } { t_2 – t_ 1 }= frac{ triangle x } { triangle t } $$
رابطه بالا مشابه چه رابطهای در ریاضی است؟ شیب. خط مستقیمی را فرض کنید که از دو نقطه $$(x_ 1 , y_1) $$ و $$ ( x_ 2 , y_2) $$ میگذرد. شیب خط برابر است با:
$$m = frac { y_2 – y_1 } { x_ 2 – x_1 } $$
رابطه فوق، مشابه رابطه سرعت، یعنی $$overline{v}= frac { x _ 2 – x_ 1 } { t_2 – t_ 1 }= frac{ triangle x } { triangle t } $$، است. در نتیجه، شیب نمودار مکان زمان، سرعت حرکت جسم را به ما میدهد. از آنجا که نمودار مکان زمان،خطی با شیبِ ثابت است، نمودار سرعت زمان برای حرکت یکنواخت، خطی افقی به صورت نشان داده شده در تصویر زیر است.
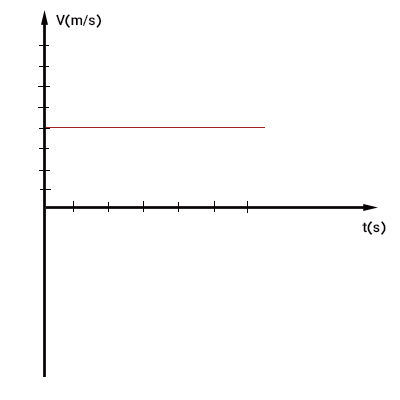
نمودار شتاب زمان در حرکت یکنواخت چیست؟
در بخش قبل فهمیدیم، نمودار سرعت زمانِ حرکت یکنواخت، خطی افقی با شیب صفر است. آیا میدانید شیب نمودار سرعت زمان، چه کمیت فیزیکی را به ما میدهد؟ شتاب. به تغییرات سرعت نسبت به زمان، شتاب میگوییم:
$$overline{a}= frac { v _ v – x_ 1 } { t_2 – t_ 1 }= frac{ triangle v } { triangle t } $$
در نتیجه، شتاب در حرکت یکنواخت روی خط راست، برابر صفر است و نمودار شتاب زمان به صورت زیر رسم میشود.
تا اینجا فهمیدیم حرکت یکنواخت چیست و نمودارهای مکان زمان، سرعت زمان و شتاب زمان آن را با یکدیگر رسم کردیم. در ادامه، فرمول حرکت یکنواخت را با یکدیگر بهدست میآوریم و مثالهایی را با یکدیگر حل میکنیم.
فرمول حرکت یکنواخت چیست؟
فرمول حرکت یکنواخت در فیزیک به صورت زیر نوشته میشود:
$$x = x_0 + v_ 0 t$$
در رابطه فوق:
- $$x$$ مکان جسم در زمان t است.
- $$x_0 $$ مکان جسم در زمان صفر است.
- $$v_0 $$ سرعت اولیه جسم است که مقدار آن با گذشت زمان تغییر نمیکند.
اندیس صفر در رابطههای فیزیک به معنای مقدار اولیه کمیت فیزیکی در زمان صفر یا در ابتدای حرکت است. گاهی به جای اندیس صفر، از حرف انگلیسی $$i$$ استفاده میشود. معادله $$x = x_0 + v_ 0 t$$ چه اطلاعاتی به ما میدهد؟ به جای حفظ کردن این معادله، بهتر است چگونگی استفاده از آن و اطلاعاتی که به شما میدهد را درک کنید. در ادامه، مفهوم معادله داده شده را قدمبهقدم با یکدیگر بررسی میکنیم.
$$x$$ مکان نهایی جسم در زمان t و واحد اندازهگیری آن متر است. به عنوان مثال، فرض کنید مسئلهای به ما داده شده که در آن اتومبیلی با سرعت ۸۰ کیلومتر بر ساعت در حال حرکت است و باید مکان اتومبیل را یک ساعت پس از شروع حرکت بهدست آوریم. $$x$$ مکان نهایی اتومبیل را پس از یک ساعت از شروع حرکت به ما میدهد. به این نکته توجه داشته باشید که با توجه به مکان اتومبیل نسبت به مبدا انتخاب شده، $$x$$ میتواند منفی یا مثبت باشد.

نکته مهم دیگری که باید به آن توجه داشته باشیم آن است که به هنگام حل مسائل مربوط به حرکت در فیزیک، جهتی را به صورت قراردادی به عنوان جهت مثبت انتخاب میکنیم. اگر جسم در خلاف جهت مثبت حرکت کند، جابجایی و سرعت آن میتوانند منفی باشند. در ادامه، این موضوع را با حل مثال بیشتر توضیح میدهیم. $$x_0 $$ مکان اولیه جسم در زمان صفر و واحد اندازهگیری آن متر است. شاید با خود فکر کنید مقدار $$x_0 $$ همواره برابر صفر است. اما اینگونه نیست. $$x_0 $$ میتواند صفر یا هر مقدار دیگری داشته باشد. در واقع، مقدار $$x_0 $$ به نوع مسئله، نقطه شروع حرکت و مبدا مختصات انتخاب شده وابسته است.
t زمانِ کل برای انجام حرکت و واحد اندازهگیری آن ثانیه و $$v_0 $$ سرعت اولیه و واحد اندازهگیری آن متر بر ثانیه است. واحد اندازهگیری کمیتها در فیزیک از اهمیت بالایی برخوردار هستند و به شما در حل مسائل مختلف فیزیکی کمک میکنند. همچنین، مقدار $$v_0 $$ در تمام طول حرکت ثابت است و علامت آن به جهت حرکت جسم وابسته است. اگر جسم در جهت مثبت انتخاب شده حرکت کند، سرعت آن مثبت و اگر در خلاف جهت مثبت حرکت کند، سرعت آن منفی است.
چگونه حرکت یکنواخت را بهتر یاد بگیریم؟
در بخشهای قبل فهمیدیم حرکت یکنواخت چیست و با فرمول آن آشنا شدیم. به حرکتی که در آن جسم با سرعت ثابت روی خطی مستقیم حرکت میکند، حرکت یکنواخت میگوییم. در حل بسیاری از مسائل مربوط به حرکت، قبل از حل مسئله باید نوع حرکت جسم را مشخص کنیم. بنابراین، تشخیص نوع حرکت بسیار مهم و ضروری است. به طور معمول، در حرکت یکنواخت، جسم روی خط مستقیم و بدون تغییر جهت، حرکت میکند. انواع حرکت در فیزیک دوازدهم یا فیزیک ۳ به طور مفصل درس داده میشود. در فصل اول این کتاب، با دو نوع حرکت، حرکت با سرعت ثابت و حرکت شتاب ثابت، آشنا میشوید.
در نگاه نخست، این دو نوع حرکت، بسیار ساده به نظر میرسند. اما مسائل مطرح شده در رابطه با آنها میتوانند بسیار پیچیده باشند. در نتیجه، درک عمیق این دو نوع حرکت برای حل مسائل مربوط به آنها بسیار مهم است. تماشای فیلمهای آموزشی، مانند فیلمهای آموزشی تهیه شده در فرادرس، میتواند به شما برای درک بهتر این حرکتها و مسائل مربوط به آنها کمک زیادی کند.
در این فیلمهای آموزشی فرادرس:
- مفاهیمی مانند سرعت، مسافت، جابجایی، شتاب، سرعت و شتاب متوسط را به طور کامل میآموزید.
- نحوه حل مسائل مربوط به حرکت یکنواخت را به صورت گامبهگام فرا میگیرید.
- توانایی شما در تحلیل و بررسی حرکت اجسام ارتقا مییابد.
- با استفاده از مثالهای کاربردی و شبیهسازیهای واقعی، درک عمیقتری از حرکت یکنواخت بهدست میآورید.
چگونه مسائل مربوط به حرکت یکنواخت را حل کنیم؟
تا اینجا میدانیم حرکت یکنواخت و فرمول آن چیست. همچنین، نمودارهای مکان زمان، سرعت زمان و شتاب زمان را برای حرکت یکنواخت روی خط مستقیم رسم کردیم. برای حل مسئلههای مربوط به حرکت یکنواخت میتوانیم گامهای زیر را به ترتیب طی کنیم.
گام اول
در بخش قبل با فرمول حرکت یکنواخت آشنا شدیم. فرمول حرکت یکنواخت به صورت زیر نوشته میشود:
$$x = x_0 + v t$$
در رابطه فوق:
- $$x$$ مکان جسم در زمان t است.
- $$x_0 $$ مکان جسم در زمان صفر است.
- $$v $$ سرعت حرکت جسم است که مقدار آن با گذشت زمان تغییر نمیکند.
رابطه فوق را میتوانیم برحسب زمان و سرعت نیز بنویسیم. در نخستین گام، باید صورت مسئله را به دقت مطالعه و کمیتهای معلوم و مجهول را مشخص کنیم.
گام دوم
پس از مشخص کردن کمیتهای مجهول و معمول، به راحتی میتوانیم معادله حرکت یکنواخت را برحسب کمیت مجهول بنویسیم و با قرار دادن کمیتهای معمول در معادله، مقدار خواسته شده را بهدست آوریم.
در این بخش و قبل از حل مثالهای مختلف در رابطه با حرکت یکنواخت، میخواهیم مثالی را به صورت کامل و با توجه به گامهای گفته شده در بالا با یکدیگر حل کنیم تا با چگونگی حل مسائل مرتبط با این نوع حرکت آشنا شوید.
مثال حرکت یکنواختِ دو قطار نسبت به یکدیگر
قطار A با سرعت ۴۵ کیلومتر بر ساعت از ایستگاه خارج میشود. دو ساعت بعد، قطار B همجهت با قطار A، همان ایستگاه را با سرعت ۵۰ کیلومتر بر ساعت ترک میکند. مسافت طی شده توسط دو قطار، پس از آنکه قطار B به قطار A میرسد، چه مقدار است؟ (دو قطار با سرعت ثابت حرکت میکنند)

پاسخ
همانطور که در صورت سوال آمده است، دو قطار با سرعت ثابت حرکت میکنند. از اینرو، حرکت آنها را میتوانیم به عنوان حرکت یکنواخت در نظر بگیریم. فرمول حرکت یکنواخت در فیزیک به صورت زیر نوشته میشود:
$$x = x_0 + v_ 0 t$$
در رابطه فوق:
- $$x$$ مکان جسم در زمان t است.
- $$x_0 $$ مکان جسم در زمان صفر است.
- $$v_0 $$ سرعت اولیه جسم است که مقدار آن با گذشت زمان ثابت است.
همانطور که در بخشهای قبل اشاره کردیم، برای حل چنین مسائلی باید نقطهای را به عنوان مبدا و جهتی را به عنوان جهت مثبت انتخاب کنیم. برای راحتی کار، ایستگاه قطار را به عنوان مبدا و جهت راست را به عنوان جهت مثبت در نظر میگیریم. در نتیجه $$x_0 $$ برابر صفر است و معادله $$x = x_0 + v_ 0 t$$ به صورت $$x = vt$$ نوشته میشود. رابطه $$x = vt$$ برای قطار A و B را به صورت زیر مینویسیم:
$$x_A = v_A t_A$$
$$x_B = v_B t_B$$
در این مثال میخواهیم مسافت طی شده توسط دو قطار، پس از رسیدن قطار B به قطار A را بهدست آوریم. دو قطار به هنگام رسیدن به یکدیگر، فاصله یکسانی از ایستگاه دارند، بنابراین $$x_A$$ با $$x_B$$ با یکدیگر برابر هستند.
$$x_A= x _B \ v_A t_A = v_B t_B $$
زمانهای $$t_A $$ و $$ t _ B $$ را نداریم. فرض کنید مقدار $$t_A $$ برابر $$x $$ است. مقدار $$t_B $$ چه مقدار است؟ بر طبق صورت مسئله، قطار B دو ساعت پس از قطار A به ایستگاه رسیده است. در نتیجه مقدار $$t_B $$ را میتوانیم به صورت زیر بنویسیم:
$$t_B = t_A -2 \ t_B = x – 2 $$
$$t_A $$ و $$ t _ B $$ را در رابطه $$v_A t_A = v_B t_B$$ قرار میدهیم:
$$v_A x = v_B (x -2 ) $$
مقدار $$v_A $$ و $$v_B $$ به ترتیب برابر ۴۵ و ۵۰ کیلومتر بر ساعت است. با قرار دادن مقدار سرعت در رابطه $$v_A x = v_B (x -2 ) $$ داریم:
$$45 x = 50 (x -2 ) \ 45 x = 50 x – 100 \ 5x = 100 \ x = frac { 100 } { 5} = 20 h$$
در نتیجه، دو قطار ۲۰ ساعت پس از خروج قطار A از ایستگاه، به یکدیگر میرسند.
$$t_1 – x = 20 h , enspace t_2 = x- 2 = 18 h $$
با قرار دادن زمان در رابطههای مربوط به $$x_A$$ یا $$x-B$$ میتوانیم مقدار آنها را بهدست آوریم.
$$x_ A = v_A t_A = 45 times 0 = 900 km $$
در نتیجه، دو قطار در فاصله ۹۰۰ کیلومتری از ایستگاه به یکدیگر میرسند. شاید از خود بپرسید چرا مکان و زمان در معادله حرکت یکنواخت برحسب متر و ثانیه نوشته نشدهاند. هنگامیکه سرعت برحسب کیلومتر بر ساعت بیان میشود، واحدهای اندازهگیری مکان و زمان به ترتیب میتوانند برحسب کیلومتر و ساعت نوشته شوند.
تمرین و مثال از حرکت یکنواخت
اکنون میدانیم مسائل مربوط به حرکت یکنواخت را چگونه حل کنیم. در ادامه، چند مثال و سپس تمرین را با یکدیگر بررسی و حل میکنیم.
حل مثال از حرکت یکنواخت
در ادامه، چند مثال از حرکت یکنواخت آورده شده است.
مثال ۱
اتومبیلی در جاده مستقیمی حرکت میکند. با توجه به نمودار مکان زمان آن، حرکت اتومبیل بین کدام دو نقطه یکنواخت است؟
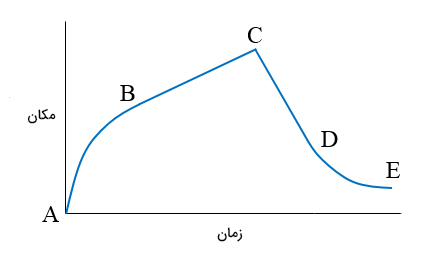
نمودار مکان زمان جسم در حرکت یکنواخت، خط مستقیمی با شیبِ ثابت است. بنابراین، در نمودار داده شده باید به دنبال نقاطی باشیم که خطی مستقیم با شیبِ ثابت از آنها میگذرد. خط عبوری از دو نقطه B و C خطی مستقیم با شیب ثابت و مثبت و خط عبوری از نقطههای C و D خطی مستقیم با شیب ثابت و منفی است. بنابراین، اتومبیل بین دو نقطه B و C و دو نقطه C و D، به صورت یکنواخت حرکت میکند. شاید از خود بپرسید، شیب منفی و مثبت در حرکت یکنواخت چه تفاوتی با یکدیگر دارند.
همانطور که در مثالهای بالا مشاهده کردید، به هنگام حل مسائل حرکتشناسی باید جهتی را به عنوان جهت مثبت انتخاب کنیم. اگر جسم در جهت مثبت قراردادی حرکت کند، سرعت آن مثبت و اگر خلاف آن حرکت کند، سرعت آن منفی است.
مثال ۲
تصویر زیر مسیر حرکت اتومبیل و نمودار سرعت زمان آن را نشان میدهد. با توجه به نمودار سرعت زمان، حرکت اتومبیل بین کدام دو نقطه یکنواخت است؟
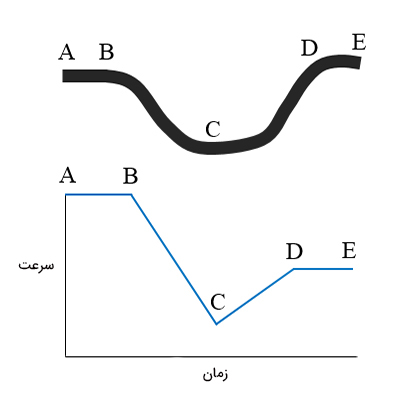
نمودار سرعت زمان جسم در حرکت یکنواخت، خط افقی با شیبِ صفر است. بنابراین، در نمودار داده شده باید به دنبال نقاطی باشیم که خطی افقی با شیبِ صفر از آنها میگذرد. خطهای عبوری از نقطههای $$(A , B)$$ و $$( D , E)$$ خطوطی افقی (موازی محور زمان) با شیب صفر هستند. بنابراین، اتومبیل بین دو نقطه A و B و دو نقطه D و E، به صورت یکنواخت حرکت میکند.
مثال ۳
در مثال ۱۲، در چه نقطهای جهت حرکت اتومبیل تغییر میکند؟
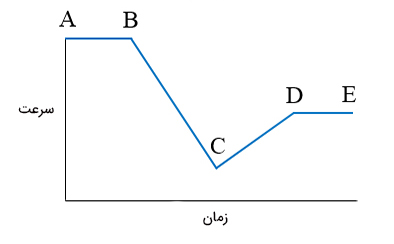
ابتدا مثال ۱۲ را با یکدیگر بررسی میکنیم. به نمودار سرعت زمان در مثال ۱۲ دقت کنید. نقاط نشان داده شده در نمودار را به صورت جداگانه بررسی میکنیم:
- نقطه A: اتومبیل از این نقطه با سرعت مشخصی شروع به حرکت میکند.
- نقطه B: اتومبیل با سرعت ثابت از نقطه A به نقطه B میرسد. در این نقطه، شیب نمودار سرعت زمانِ اتومبیل تغییر میکند و منفی میشود. شیب نمودار سرعت زمان، برابر کمیتی به نام شتاب است. به تغییرات سرعت برحسب زمان، شتاب میگوییم. شیب منفی به معنای آن است، که راننده از سرعت خود میکاهد.
- نقطه C: به نمودار در این نقطه دقت کنید. شیب نمودار سرعت زمان قبل از نقطه C منفی و پس از این نقطه، مثبت است. راننده قبل از رسیدن به نقطه C از سرعت خود میکاهد و با شیب منفی حرکت میکند. اما پس از عبور از این نقطه، بر سرعت خود میافزاید و با شیب مثبت به حرکت خود ادامه میدهد. در نتیجه، جهت حرکت اتومبیل در نقطه C تغییر میکند.
مثال ۴
فرض کنید برای رفتن به مهمانی باید به خانه دوستتان در شهر دیگری در ۶۰ کیلومتری شهر خود بروید. به هنگام رفت، به دلیل تصادف، ترافیک سنگینی در اتوبان وجود دارد. بنابراین، پس از دو ساعت به مهمانی میرسید. به هنگام بازگشت، ترافیک سنگینی وجود ندارد، بنابراین پس از یک ساعت رانندگی به خانه خواهید رسید. تندی متوسط در مسیر رفتوبرگشت چه مقدار است؟
در این مثال، حرکتی رفتوبرگشتی گفته شده است. شما برای رفتن به خانه دوستتان، مسیر رفت را در دو ساعت و مسیر بازگشت را در یک ساعت طی کردهاید. به این نکته توجه داشته باشید که تندی کمیتی نردهای است و تنها اندازه دارد. بنابراین، برای محاسبه آن به جهت حرکت توجه نمیکنیم. تندی از تقسیم مسافت طی شده توسط جسم به زمان لازم برای طی کردن مسافت بهدست میآید. تندی رفت برابر است با:
$$s = frac {distance} { time} = frac { 60 km } { 2 h } = 30 frac { km } { h } $$
تندی بازگشت نیز به صورت زیر بهدست میآید:
$$s = frac {distance} { time} = frac { 60 km } { 1 h } = 60 frac { km } { h } $$
تمرین حرکت یکنواخت
در ادامه چند تمرین از حرکت یکنواخت را بررسی میکنیم.
تمرین ۱
سارا برای شرکت در کنفرانس به شهری در فاصله ۱۲۰ کیلومتری رفت. او به هنگام بازگشت و به دلیل بازسازی بخشی از اتوبان مجبور شد سرعت رانندگی خود را ۱۰ کیلومتر بر ساعت کاهش دهد. بنابراین، مدت زمان بازگشت سارا ۲ ساعت طولانیتر از مدت زمان رفت او شد. مقدار تندی رانندگی سارا به هنگام رفت چه مقدار بود؟
۳۰ کیلومتر بر ساعت
۲۰ کیلومتر بر ساعت
۲۰- کیلومتر بر ساعت
۴۰ کیلومتر بر ساعت
برای حل این مثال میتوانیم جدولی تهیه کنیم و اطلاعات داده شده را در آن قرار دهیم.
| سرعت | زمان | مسافت | |
| حرکت به سمت کنفرانس | $$v$$ | t | 120 |
| بازگشت از کنفرانس | $$v- 10 $$ | t+2 | 120 |
برطبق صورت سوال، سارا به هنگام بازگشت از کنفرانس، سرعت رانندگی خود را ۱۰ کیلومتر بر ساعت کاهش داد و ۲ ساعت دیرتر از زمان رفت به مقصد رسید. همانطور که گفتیم حرکت یکنواخت با استفاده از رابطه زیر بهدست میآید:
$$x = x_0 + v_ 0 t$$
در رابطه فوق:
- $$x$$ مکان جسم در زمان t است.
- $$x_0 $$ مکان جسم در زمان صفر است.
- $$v_0 $$ سرعت اولیه جسم است که مقدار آن با گذشت زمان تغییر نمیکند.
برای حل چنین مسائلی باید نقطهای را به عنوان مبدا و جهتی را به عنوان جهت مثبت انتخاب کنیم. شهری که سارا از آن حرکت میکند را به عنوان مبدأ و جهت حرکت از شهر به محل کنفرانس را به عنوان جهت مثبت انتخاب میکنیم.
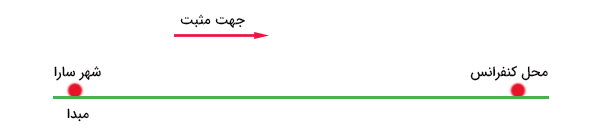
در نتیجه، معادله حرکت به هنگامِ رفت به صورت زیر نوشته میشود:
$$x_1 =x_0 + v_1 t_1 \120 = v_1 t_1$$
به هنگام بازگشت، سارا در فاصله ۱۲۰ کیلومتری از مبدا قرار دارد و در خلاف جهت مثبت حرکت میکند. بنابراین، معادله حرکت به هنگام بازگشت به صورت زیر نوشته میشود:
$$0 = 120 – v_2 t_2 $$
اگر سرعت و زمان را به ترتیب به هنگام رفت برابر $$v$$ و $$t $$ بگیریم، سرعت و زمان به ترتیب به هنگام بازگشت برابر $$v-10 $$ و $$t+2 $$ هستند. در نتیجه معادلههای رفت و برگشت را میتوانیم به صورت زیر بنویسیم:
$$120 = vt \ 0 = – ( v – 10 ) ( t + 2 ) + 120 \ begin{cases}120 = vt \ 120 = (v- 10) (t +10) end{cases} $$
دو معادله و دو مجهول داریم که مقدار آنها را به صورت زیر بهدست میآوریم:
$$ begin{cases}120 = vt \ 120 = (v- 10) (t +10) end{cases} \t = frac { 120 } { v } \ 120 = (v -1 0 ) (frac { 120 } { v } +2 ) \120 = ( v – 10 ) ( frac { 120 + 2v } { v } ) \ 120 v = (v – 10 ) ( 120 + 2 v ) \ 60 v = ( v – 10 ) ( 60 + v) \ 60 v = 60 v – 600 + v ^ 2 – 10 v \ v ^ 2 – 10 v – 60 = 0 \ ( v +20 ) ( v – 30 ) = 0 \ v = -20 frac { km } {h } , enspace v = 30 frac { km } { h } $$
از آنجا که مقدار تندی همواره مثبت است، پاسخ ۳۰ کیلومتر بر ساعت خواهد بود. شاید از خود بپرسید آیا مقدارهای تندی و سرعت با یکدیگر برابر هستند یا خیر. از آنجا که در حرکت یکنواخت، جابجایی و مسافت با یکدیگر برابر هستند، تندی و سرعت نیز مقادیر یکسانی دارند.
تمرین ۲
دو اتومبیل، همزمان و از نقطه یکسانی در جهتهای مخالف شروع به حرکت میکنند. اتومبیل یک ۱۵ کیلومتر بر ساعت سریعتر از اتومبیل دو حرکت میکند (اتومبیل یک به سمت راست و اتومبیل دو به سمت چپ حرکت میکند). اگر پس از دو ساعت فاصله دو اتومبیل از یکدیگر برابر ۳۷۰ کیلومتر باشد، سرعت هر یک از آنها چه مقدار است؟
اتومبیل یک با سرعت ۱۰۰ کیلومتر بر ساعت به سمت راست و اتومبیل دو با سرعت ۸۵ کیلومتر بر ساعت به سمت چپ حرکت میکنند.
اتومبیل یک با سرعت ۱۱۵ کیلومتر بر ساعت به سمت راست و اتومبیل دو با سرعت ۱۰۰ کیلومتر بر ساعت به سمت چپ حرکت میکنند.
اتومبیل یک با سرعت ۸۵ کیلومتر بر ساعت به سمت راست و اتومبیل دو با سرعت ۷۰ کیلومتر بر ساعت به سمت چپ حرکت میکنند.
رابطه مکان برحسب زمان در حرکت یکنواخت به صورت $$x = x_0 + vt $$ نوشته میشود. دو اتومبیل از نقطه O شروع به حرکت میکنند. اتومبیل یک با سرعت $$v_1 $$ از این نقطه شروع به حرکت میکند و به سمت راست میرود. اتومبیل دو نیز با سرعت $$v_ 2 $$ شروع به حرکت به سمت چپ میکند. پس از گذشت دو ساعت، فاصله اتومبیل یک از نقطه O برابر $$x_1 $$ و فاصله اتومبیل دو از نقطه O برابر $$x_ 2 $$ است. همچنین، نقطه O را به عنوان مرکز و جهت راست را به عنوان جهت مثبت، انتخاب میکنیم.
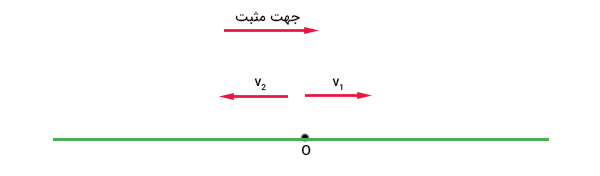
با توجه به صورت سوال میدانیم که فاصله دو اتومبیل پس از دو ساعت از شروع حرکت برابر ۳۷۰ کیلومتر است. بنابراین، مجموع $$x_ 1 $$ و $$x_2 $$ برابر ۳۷۰ کیلومتر خواهد بود.
$$x_ 1 + x_ 2 = 370 km $$
سرعت اتومبیل یک ۱۵ کیلومتر بر ساعت بیشتر از اتومبیل دو است. بنابراین، اگر اتومبیل یک با سرعت $$v$$ کیلومتر بر ساعت حرکت کند، سرعتِ اتومبیل دو برابر $$v – 15 $$ کیلومتر بر ساعت خواهد بود. معادله حرکت اتومبیلهای یک و دو در ادامه نوشته شده است:
$$begin{cases}x_1 = v_1 t_1 Rightarrow x_1 = vt_1 \ -x_2 = – v_2 t_2 Rightarrow x_2 = – (v – 15 ) t _2 end{cases}$$
شاید از خود بپرسید چرا معادله اتومبیل دو، منفی دارد. دلیل این مورد آن است که اتومبیل دو در خلاف جهت مثبت قراردادی حرکت میکند و مکان $$x_2 $$ قبل از مبدا انتخاب شده قرار دارد، بنابراین سرعت و مکان آن منفی هستند. رابطه بین $$x_1 $$ و $$x_2 $$ را میدانیم. برای حل معادلات بالا، به معادله دیگری نیز نیاز داریم. از آنجا که فاصله دو اتومبیل پس از گذشت دو ساعت برابر ۳۷۰ کیلومتر میشود، بنابراین زمانهای $$t_1 $$ و $$t_2 $$ با یکدیگر برابر و مساوی ۲ ساعت هستند.
$$t_1 = t_ 2 = 2 h $$
اکنون به راحتی میتوانیم سرعت حرکت هر اتومبیل را جداگانه بهدست آوریم.
$$ begin{cases}x_1 = v_1 t_1 Rightarrow x_1 = vt_1 \ -x_2 = – v_2 t_2 Rightarrow x_2 = (v – 15 ) t _2 end{cases} \ t_1=t_2 = 2 h \ begin{cases} x_1 = 2v \ x_2 = 2 (v – 15 ) end{cases} \ x_1 + x_2 = 2v + 2 ( v -15) \ 370 = 4v – 30 \ 400 = 4v \ v = 100 frac { km } { h } $$
در نتیجه، اتومبیل یک با سرعت ۱۰۰ کیلومتر بر ساعت به سمت راست و اتومبیل دو با سرعت ۸۵ کیلومتر بر ساعت به سمت چپ حرکت میکنند.
تمرین ۳
قطار A ساعت یک بعدازظهر با سرعت ۶۰ کیلومتر بر ساعت از ایستگاه قطار خارج میشود. یک ساعت بعد قطار سریعالسیرِ B، همان ایستگاه را با سرعت ۹۰ کیلومتر بر ساعت ترک میکند. قطار B چند ساعت پس از شروع حرکت به قطار A میرسد؟ (قطارها در دو ریل موازی حرکت میکنند، بنابراین هیچ تصادفی رخ نمیدهد)
قطار B سه ساعت پس از خروج از ایستگاه به قطار A میرسد.
قطار B یک ساعت پس از خروج از ایستگاه به قطار A میرسد.
قطار B دو ساعت پس از خروج از ایستگاه به قطار A میرسد.
قطار B چهار ساعت پس از خروج از ایستگاه به قطار A میرسد.
اگر زمان حرکت قطار A را t در نظر بگیریم، زمان حرکت قطار B برابر t-1 خواهد بود. زیرا قطار B یک ساعت پس از قطار A از ایستگاه قطار خارج شده است.
$$t_A = t \ t_B = t -1 $$
قطار A با سرعت ۶۰ کیلومتر بر ساعت و قطار B با سرعت ۹۰ کیلومتر بر ساعت و هر دو به سمت راست حرکت میکنند، بنابراین جهت راست را به عنوان جهت مثبت انتخاب میکنیم. همچنین، ایستگاه قطار را به عنوان مبدا در نظر میگیریم. از آنجا که دو قطار از ایستگاه شروع به حرکت کردهاند، مکان اولیه آنها برابر صفر است. همچنین، بردار سرعت آنها به سمت راست و در جهت مثبت قرار دارد. با توجه به اطلاعات فوق، معادله حرکت دو قطار به صورت زیر نوشته میشود:
$$ begin{cases}x_A = v_A t_A Rightarrow x_A = 60t \ x_B = v_Bt_B Rightarrow x_B = 90 ( t -1) end{cases}$$
هنگامیکه دو قطار به هم برسند، مکان آنها با یکدیگر برابر میشود:
$$ x_A = x_B \ 60t = 90 (t -1 ) \ 60 t = 90t – 90 \ 30t = 90 \ t = 3 h $$
در نتیجه، قطار B دو ساعت پس از خروج از ایستگاه به قطار A میرسد.
تمرین ۴
سیمین برای خرید نرمافزاری از خانه خارج و به نزدیکترین فروشگاه نرمافزارهای کامپیوتری میرود. به دلیل ترافیک شدید، سیمین با سرعت متوسطی برابر ۱۵ کیلومتر بر ساعت رانندگی میکند. اما به هنگام بازگشت به خانه و به دلیل کاهش ترافیک، او میتواند با سرعت ۳۵ کیلومتر بر ساعت رانندگی کند. اگر مدت زمان رفت و برگشت برابر ۲ ساعت باشد، مدت زمانی که سیمین از خانه تا فروشگاه رانندگی میکند، چه مقدار است؟
حرکت سیمین را میتوان به دو مرحله تقسیم کرد:
- حرکت با سرعت ۱۵ کیلومتر بر ساعت از خانه به فروشگاه
- حرکت با سرعت ۳۵ کیلومتر بر ساعت از فروشگاه به خانه
حرکت مرحله اول در تصویر زیر نشان داده شده است. خانه و جهت راست را به ترتیب به عنوان مبدا و جهت مثبت انتخاب میکنیم.

معادله حرکت در مرحله اول به صورت زیر نوشته میشود:
$$x_ 1 = v_ 1 t_ 1 \ x_ 1 = 15 t_ 1 $$
حرکت مرحله دوم نیز در تصویر زیر نشان داده شده است. در این مرحله، مکان اولیه سیمین برابر $$ x_{0,2} $$ و مکان نهایی آن برابر صفر است. همچنین، سرعت حرکت اتومبیل در مرحله دوم در خلاف جهت مثبت است، بنابراین علامتِ سرعت در این مرحله منفی خواهد بود.

معادله حرکت در مرحله دوم به صورت زیر نوشته میشود:
$$x_2 = x_ { 0, 2 } + v_ 2 t_ 2 \ 0 = x_ { 0 , 2 } + v_2 t_ 2= x_ { 0 , 2 } – 35 t_ 2 \ x_ { 0 , 2 } = 35 t_ 2 $$
برطبق صورت سوال، مدت زمان رفت و برگشت سیمین برابر ۲ ساعت است.
$$ t _1 + t _ 2 = 2 h $$
همچنین، $$x_ { 0 , 2 } $$ و $$ x_1 $$ با یکدیگر مساوی و برابر فاصله خانه تا فروشگاه است:
$$t_1 + t_2 = 2 h , enspace 35t_2 = 15t_1 \ 35 t_2 = 15 ( 2 – t_2) Rightarrow 35 t_2 = 30 – 15 t_ 2 \ 50 t_2 = 30 \ t_2 = frac { 30 } { 50 } h = frac { 3 } { 5 } h , enspace t_ 1 = 2 – frac { 3} { 5 } = frac { 7 } { 5 } h $$
بنابراین، زمان رفت سیمین، برابر ۱٫۴ ساعت و زمان بازگشت او برابر ۰٫۶ ساعت است.
تمرین ۵
دو خواهر به نامهای یلدا و نگین همزمان از خانه خارج و برای رفتن به مدرسه و دانشگاه در دو جهت مخالف شروع به حرکت میکنند. سرعت حرکت یلدا ۲ متر بر ثانیه بیشتر از سرعت حرکت نگین است. پس از ۳۰ دقیقه، فاصله آنها از یکدیگر برابر ۵ کیلومتر خواهد بود. سرعت حرکت نگین و یلدا به ترتیب برابر است با:

سرعت حرکت نگین و یلدا به ترتیب برابر ۲٫۸ و ۰٫۸ متر بر ثانیه است.
سرعت حرکت نگین و یلدا به ترتیب برابر ۰٫۸ و ۲٫۸ متر بر ثانیه است.
سرعت حرکت نگین و یلدا برابر ۲٫۸ متر بر ثانیه است.
سرعت حرکت نگین و یلدا برابر ۰٫۸ متر بر ثانیه است.
بر طبق صورت سوال، یلدا و نگین همزمان از خانه خارج و در دو جهت مخالف شروع به حرکت میکنند. سرعت حرکت یلدا ۲ متر بر ثانیه بیشتر از سرعت حرکت نگین است. اگر پس از ۳۰ دقیقه، فاصله آنها از یکدیگر برابر ۵ کیلومتر باشد، هر کدام با چه سرعتی حرکت میکنند؟ یلدا و نگین با سرعت ثابت حرکت میکنند، بنابراین حرکت آنها یکنواخت و فرمول حرکت برابر $$x = x_0 + v t $$ است. یلدا و نگین همزمان از خانه خارج میشوند، در نتیجه برای راحتی کار میتوانیم خانه و مکان اولیه آنها را برابر مبدا در نظر بگیریم:
$$ x_ 0 $$
در ادامه، معادله حرکت هر کدام را جداگانه مینویسیم. معادله حرکت نگین به صورت $$x_ N = v_ N t$$ و معادله حرکت یلدا نیز به صورت $$x_Y = v_ Y t$$ نوشته میشوند. سرعت حرکت یلدا، $$ v _ Y $$، دو متر بر ثانیه بزرگتر از سرعت حرکت نگین، $$ v _ N $$، است.
$$ v_ Y = v_ N + 2 $$
همچنین، زمان نهایی برابر ۳۰ دقیقه است و پس از گذشت این مدت زمان، یلدا و نگین در فاصله ۵ کیلومتری از یکدیگر قرار گرفتهاند:
$$x_Y + x_N = 5 km $$
از آنجا که سرعت برحسب متر بر ثانیه داده شده است، مکان نیز باید برحسب متر باشد:
$$x_ Y + x_ N = 5000 m$$
با توجه به اطلاعات فوق، معادله حرکت نگین و یلدا را میتوانیم به صورت زیر بنویسیم:
$$x_ N = v_ N t Rightarrow x_N = 1800 v_ N \ x_ Y = v_ Y t Rightarrow x_ Y = 1800 ( v_ N + 2 ) $$
از آنجا که $$x_ Y + x_ N = 5000 m$$، دو رابطه فوق را با یکدیگر جمع میکنیم:
$$ \ x_ N + x_ Y = 1800 v_ N + 1800 ( v_ N + 2) \ 5000 = 1800 v_ N + 1800 v_ N + 3600 \ 5000 – 3600 = 3600 v _ N \ 2400 = 3600 v_ N \ v_N = frac { 2400 } { 3600} = frac { 24 } { 30 } =frac { 4 } { 5 } = 0.8 frac { m } { s } $$
با داشتن سرعت نگین، سرعت حرکت یلدا برابر ۲٫۸ متر بر ثانیه بهدست میآید.
تمرین ۶
دو قطار همزمان از ایستگاه قطار شروع به حرکت میکنند. قطار A با سرعت ۴۵ کیلومتر بر ساعت به سمت غرب و قطار B با سرعت ۵۰ کیلومتر بر ساعت به سمت شرق حرکت میکند. پس از چند ساعت، فاصله دو قطار از یکدیگر برابر ۱۴۲٫۵ کیلومتر میشود؟

دو قطار A و B همزمان و در دو جهت مخالف، از ایستگاه قطار خارج میشوند:
- قطار A با سرعت ۴۵ کیلومتر بر ساعت به سمت غرب حرکت میکند.
- قطار B با سرعت ۵۰ کیلومتر بر ساعت به سمت شرق حرکت میکند.
برای حل این مثال، چند نکته را باید در نظر بگیریم:
- ایستگاه قطار را به عنوان مکان اولیه قطارها انتخاب میکنیم و مبدا مختصات در نظر میگیریم:
$$x_{A,0} = x_{ B,o } = 0$$
- جهت شرق را به عنوان جهت مثبت در نظر میگیریم. بنابراین سرعت حرکت قطار A برابر ۴۵- کیلومتر بر ساعت و سرعت حرکت قطار B برابر ۵۰+ کیلومتر بر ساعت است.
برای داشتن درک بهتری از حل مثال، حرکت قطارها به صورت تصویری در ادامه نشان داده شده است.
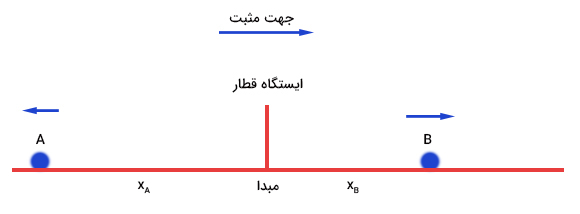
معادله حرکت هر یک از قطارها به صورت زیر نوشته میشود:
$$x_ A = x_{A,o} + v_A t Rightarrow -x_A = 0 – 45 t Rightarrow x_A = 45 t \ x_ B = x_{B,o} + v_B t Rightarrow x_B = 0 + 50 t Rightarrow x_B = 50 t$$
پس از گذشت زمان t فاصله دو قطار از یکدیگر برابر ۱۴۲٫۵ کیلومتر میشود:
$$x_A + x_ B = 142.5 km \ 50 t + 45 t = 142.5 \ 95 t = 142.5 \ t = frac { 142.5 } { 95 } = 1.5 h $$
در نتیجه، پس از گذشت ۱٫۵ ساعت فاصله دو قطار از یکدیگر برابر ۱۴۲٫۵ کیلومتر میشود.
تمرین ۷
دو اتوبوس A و B همزمان، از دو شهر مختلف به فاصله ۲۱۰ کیلومتر از یکدیگر حرکت میکنند. سرعت اتوبوس A، پنج کیلومتر بر ساعت بیشتر از سرعت اتوبوس B است. اگر دو اتوبوس دو ساعت پس از شروع حرکت به یکدیگر برسند، تندی حرکت آنها کدام است؟
اتوبوس A با تندی ۵۰ کیلومتر بر ساعت و اتوبوس B با تندی ۵۵ کیلومتر بر ساعت حرکت میکنند.
اتوبوس A با تندی ۵۵ کیلومتر بر ساعت و اتوبوس B با تندی ۵۰ کیلومتر بر ساعت حرکت میکنند.
اتوبوس A با تندی ۵۰ کیلومتر بر ساعت و اتوبوس B با تندی ۶۵ کیلومتر بر ساعت حرکت میکنند.
اتوبوس A با تندی ۶۰ کیلومتر بر ساعت و اتوبوس B با تندی ۶۵ کیلومتر بر ساعت حرکت میکنند.
همانطور که در تصویر زیر مشاهده میکنید، دو شهر A و B در فاصله ۲۱۰ کیلومتری از یکدیگر قرار گرفتهاند. اتوبوس A از شهر A و اتوبوس B از شهر B همزمان شروع به حرکت میکنند و پس از دو ساعت به یکدیگر میرسند. همانطور که در تصویر فوق مشاهده میکنید، جهت راست به عنوان جهت قراردادی مثبت و شهر A به عنوان مبدا انتخاب شدهاند.
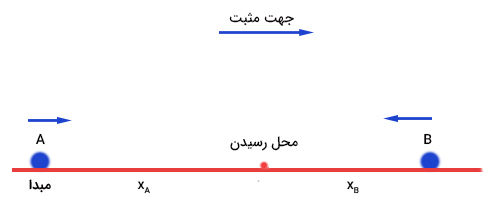
معادله حرکت یکنواخت جسم به صورت زیر نوشته میشود:
$$x = x_ o + v t $$
با انتخاب شهر A به عنوان مبدا و جهت راست به عنوان جهت مثبت، معادله حرکت اتوبوس A به صورت زیر نوشته میشود:
$$x_ A = x_ { A,o} + v_A t rightarrow x_A = 0 + v_A t \ x_ A = v_ A t $$
همچنین، معادله حرکت اتوبوس B نیز به صورت زیر نوشته میشود:
$$x_ B = x_ { B,o} + v_B t rightarrow x_B = 210 – v_B t $$
با توجه به صورت سوال، سرعت اتوبوس A، پنج کیومتر بر ساعت بیشتر از سرعت اتوبوس B است:
$$v_A = v_B + 5 $$
با ترکیب معادلات بهدست آمده، تندی حرکت هر یک از اتوبوسها را به صورت زیر بهدست میآوریم:
$$x_A = v_ A t \ x_B = 210 – v_B t \ v_A = v_B + 5 rightarrow v_ B = v_A – 5 \ t = 2 h \ x_ A = x_ B \ 210 – ( v_A – 5 ) (2) = 2 v_A \ 210 +10 = 4 v_ A rightarrow v_ A = frac { 220 } { 4 } = 55 frac { km } { h } , v_ B = 50 frac { km } { h } $$
توجه به این نکته مهم است که در حرکت یکنواخت، تندی و سرعت با یکدیگر برابر هستند.
تمرین ۸
اتومبیلی با سرعت ۷۲ کیلومتر بر ساعت از چهارراهی عبور و ۱۰ ثانیه بعد موتورسواری با سرعت ۲۵ متر بر ثانیه از همان چهارراه و در همان جهت عبور میکند. موتور سوار از لحظه عبور از چهار راه، بعد از چند ثانیه به اتومبیل میرسد؟
برای حل این مثال، ابتدا باید صورت سوال را به خوبی متوجه شویم. اتومبیلی با سرعت ۷۲ کیلومتر بر ثانیه از چهارراهی عبور و ۱۰ ثانیه بعد، موتورسواری با سرعت ۲۵ متر بر ثانیه از همان چهارراه عبور میکند. در نخستین گام، سرعت اتومبیل را از کیلومتر بر ساعت به متر بر ثانیه تبدیل میکنیم.
$$72 frac { km } { h } times frac { 1 h } { 3600 s } times frac { 1000 m } { 1 km } = 72 times frac { 10 } { 36 } = 20 frac { m } { s } $$
در ادامه و برای داشتن تصویری درست از حرکت اتومبیل و موتور، مسیر حرکت آنها را به صورت تصویری نشان میدهیم.
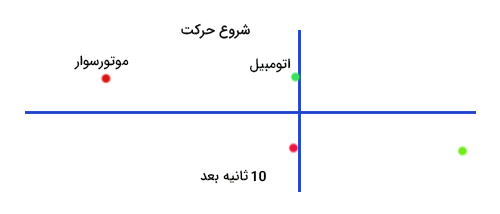
ابتدا معادله حرکت اتومبیل را مینویسیم.
$$x_A = x_ { A , o } + v_A t $$
با انتخاب چهارراه به عنوان مبدا و جهت راست به عنوان جهت مثبت، معادله فوق را به صورت زیر مینویسیم:
$$x_A = 20 t $$
معادله حرکت موتور را نیز میتوانیم به صورت زیر بنویسیم:
$$x_ M = – x_ { M, o } + v_ M t \ x_ M =- x_ { M, o } + 25 t $$
موتور پس از ۱۰ ثانیه به چهارراه (مبدا) میرسد. بنابراین، به راحتی میتوانیم $$ x_ { M, o } $$ را بهدست آوریم:
$$ 0 = – x_ { M, o } + 25 times 10 \ x_ { M , o } = 250 m \ x_ M = -250 + 25 t $$
مکانهای اتومبیل و موتور، پس از رسیدن موتور به اتومبیل با یکدیگر برابر میشوند:
$$x_ M = x_ A = -250 + 25 t = 20 t \ 5t = 250 \ t = 50 s $$
آیا موتور ۵۰ ثانیه پس از عبور از چهارراه به اتومبیل میرسد؟ خیر، موتورسوار ۵۰ ثانیه پس از شروع حرکت و ۴۰ ثانیه پس از عبور از چهارراه به اتومبیل میٰرسد.
تمرین ۹
موتورسیکلتی با سرعت ثابتی از شهر الف به شهر ب و به طور همزمان خودرویی از شهر ب به شهر الف با سرعت ثابت، حرکت میکنند. اگر فاصله بین دو شهر ۲۴۰ کیلومتر باشد و موتورسیکلت با سرعت ۶۰ کیلومتر بر ساعت و خودرو با سرعت ۸۰ کیلومتر بر ساعت حرکت کنند، چه زمانی دو وسیله در مسیر به یکدیگر میرسند؟

موتورسواری در شهر الف و در فاصله ۲۴۰ کیلومتری از شهر ب قرار دارد. این موتورسوار با سرعت ۶۰ کیلومتر بر ساعت به طرف شهر ب و همزمان، اتومبیلی از شهر ب با سرعت ۸۰ کیلومتر بر ساعت به سمت شهر الف شروع به حرکت میکند.
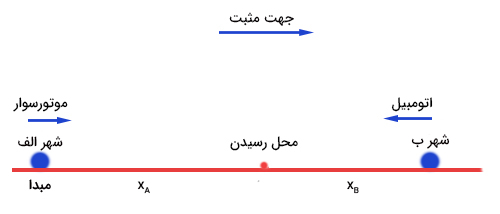
همانطور که در تصویر فوق مشاهده میکنید، جهت راست به عنوان جهت قراردادی مثبت و شهر A به عنوان مبدا انتخاب شدهاند. معادله حرکت یکنواخت جسم به صورت زیر نوشته میشود:
$$x = x_ o + v t $$
با انتخاب شهر الف به عنوان مبدا و جهت راست به عنوان جهت مثبت، معادله حرکت موتورسیکلت به صورت زیر نوشته میشود:
$$x_ M = x_ { M , o} + v_M t rightarrow x_M = 0 + v_M t \ x_ A = 60t $$
همچنین، معادله حرکت اتومبیل نیز به صورت زیر نوشته میشود:
$$x_ A = x_ { A , o} + v_A t rightarrow x_B = 240 – 80 t $$
با برابر قرار دادن مکانهای اتومبیل و موتورسیکلت، زمان رسیدن آنها به یکدیگر را بهدست میآوریم:
$$x_M = x_ A \ 60 t = 240 – 80 t \ 120 t = 240 \ t = 1.7 h$$
تمرین ۱۰
علی و سعید مهمان کاوه هستند. علی به دلیل قراری ضروری، ساعت ۴ بعدازظهر خانه کاوه را ترک و با سرعت ۶۰ کیلومتر بر ساعت به سمت محل قرار رانندگی میکند. ۲ ساعت بعد، سعید نیز از خانه کاوه خارج میشود. اگر سعید با سرعت ۸۰ کیلومتر بر ساعت رانندگی کند، چند ساعت بعد به محل قرارِ علی میرسد؟
خانه کاوه را به عنوان مبدا و حرکت به سمت راست را به عنوان جهت مثبت انتخاب میکنیم. معادله حرکت علی به صورت زیر نوشته میشود:
$$x_ A = x_ { A,o} + v_A t rightarrow x_A = 0 + v_A t \ x_ A = 60 t _A$$
همچنین، معادله حرکت سعید نیز به صورت زیر نوشته میشود:
$$ x_ S = x_ { S,o} + v_S t rightarrow x_B = 80 t _B $$
سعید، دو ساعت پس از علی، از خانه کاوه خارج شده است:
$$t_A = t + 2 \ t_ S = t $$
در نتیجه، معادله حرکت علی به صورت $$x_ S = 60 ( t + 2 ) $$ نوشته میشود. با برابر قرار دادن مکانهای علی و سعید با یکدیگر داریم:
$$x_ A = x_ S \ 60 ( t + 2 )= 80 ( t ) \ 60 t + 120 = 80 t \ 20 t = 120 \ t = 6 $$
حرکت یکنواخت دایره ای چیست؟
در بخشهای قبل فهمیدیم حرکت یکنواخت روی خط مستقیم چیست. در این بخش، در مورد حرکت یکنواخت روی دایره صحبت میکنیم. آیا تا به حال سوار چرخوفلک شدهاید؟ چرخوفلک با سرعت ثابتی میچرخد و شما روی مسیری به شکل دایره حرکت میکنید. اگر سرعت چرخش چرخوفلک تغییر نکند، حرکت شما به عنوان حرکت دایرهای یکنواخت شناخته میشود. در حالت کلی، به حرکت جسم روی مسیری به شکل دایره، حرکت دایرهای گفته میشود. قطار اسباب بازی که بر روی ریل دایرهای حرکت میکند، چرخش زمین به دور خورشید، و حرکت الکترون به دور هسته مثالهایی از حرکت دایرهای هستند.
برای آنکه حرکت دایرهای یکنواخت را به خوبی درک کنیم به کلمات تشکیلدهنده آن، یعنی حرکت، دایره و یکنواخت، به صورت جداگانه دقت میکنیم. حرکتشناسی یکی از اصلیترین شاخههای فیزیک به شمار میرود. به تغییر موقعیت جسم نسبت به زمان، حرکت گفته میشود. حرکت دایرهای بدان معنا است که جسم روی مسیری به شکل دایره و حرکت دایرهای یکنواخت به معنی آن است که جسم روی مسیری به شکل دایره با تندی ثابت حرکت میکند. این حالت، مشابه حرکت یکنواخت روی خط راست است، با این تفاوت که مسیر حرکت جسم به جای خط مستقیم، دایرهای با شعاع مشخص است.
فرض کنید توپ کوچکی را به نخ بستهایم و سر نخ را در دست خود نگه داشتهایم. با حرکت دادن نخ، توپ را روی مسیری به شکل دایره به حرکت درمیآوریم. توپ با تندی ثابت حرکت میکند. همانطور که در ابتدای مطلب گفتیم، حرکت با تندی ثابت بدان معنا است که جسم در زمانهای برابر، مسافت یکسانی را طی میکند. پنکه سقفی را به صورت نشان داده شده در تصویر زیر در نظر بگیرید که جسم کوچکی به عنوان نشانه به آن چسبانده شده است.

پنکه شروع به چرخیدن میکند و پس از گذشت مدت زمان مشخصی به تندی ثابتی میرسد و با همان تندی به چرخش خود ادامه میدهد. به جسم زردرنگ دقت کنید. این جسم روی مسیری به شکل دایره با تندی ثابت (تندی پنکه) حرکت میکند. سوال مهمی که ممکن است مطرح شود آن است که چگونه میتوانیم تندی را در حرکت دایرهای یکنواخت محاسبه کنیم. تندی از تقسیم مسافت بر زمان لازم برای طی کردن آن مسافت، بهدست میآید. فرض کنید جسمی پس از t ثانیه، یک دور کامل روی مسیر دایرهای میچرخد. مسافت طی شده توسط جسم در مدت زمان t چه مقدار است؟
جسم روی محیط دایره حرکت میکند، بنابراین مسافت طی شده توسط آن برابر محیط دایره، $$ 2 pi r $$ است. در نتیجه، مقدار تندی در حرکت دایرهای برابر است با:
$$s = frac { 2 pi r } { t } $$
تندی جسم در حرکت دایرهای یکنواخت، ثابت است. همانطور که در مطالب بالا بیان شد، تندی و سرعت در حرکت یکنواخت روی خط راست با یکدیگر برابر هستند. سوال مهمی که ممکن است مطرح شود آن است که آیا این دو کمیت در حرکت دایرهای یکنواخت نیز با یکدیگر برابر هستند. خیر، تندی و سرعت در حرکت دایرهای یکنواخت با یکدیگر برابر نیستند. تعریف تندی و سرعت را به یاد بیاورید. تندی کمیتی اسکالر است که تنها اندازه دارد. اما سرعت، کمیتی برداری با اندازه و جهت است. به بیان دیگر، سرعت را به عنوان تندی تعریف میکنیم که جهت دارد. اندازه تندی در حرکت دایرهای یکنواخت ثابت است. آیا جهت حرکت نیز ثابت است؟ خیر.
از آنجا که جهت حرکت جسم به هنگام حرکت روی مسیر دایرهای تغییر میکند، سرعت آن نیز تغییر خواهد کرد. سرعت، اندازه و جهت دارد. برای آنکه سرعت حرکت جسمی به هنگام حرکت ثابت باشد، اندازه و جهت سرعت باید بدون تغییر باقی بمانند. این حالت در حرکت روی خط راست رخ میدهد. در مقابل، در حرکت دایرهای، اندازه سرعت ثابت است، اما جهت حرکت به طور پیوسته تغییر میکند. در نتیجه، سرعت در حرکت دایرهای یکنواخت ثابت نیست، اما تندی ثابت است. بار دیگر حرکت دایرهای توپِ متصل به نخ را در نظر بگیرید. جهت حرکت توپ در هر لحظه چگونه است؟ سرعت توپ در هر نقطه از مسیر، بر دایره مماس است.
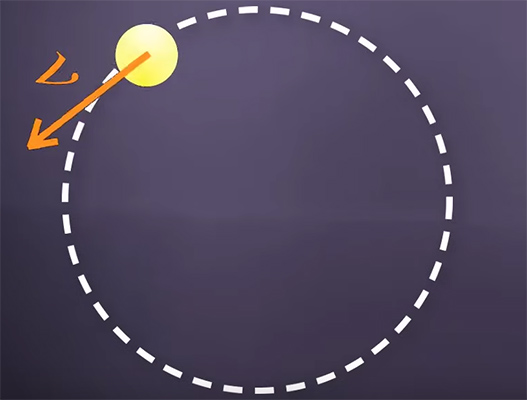
تا اینجا میدانیم در حرکت دایرهای یکنواخت، تندی ثابت، اما سرعت متغیر است. به این نکته توجه داشته باشید که اندازه سرعت ثابت باقی میماند، اما جهت آن به طور پیوسته با زمان تغییر خواهد کرد. در نتیجه، سرعت را متغیر در نظر میگیریم. آیا مقدار شتاب در حرکت دایرهای یکنواخت صفر است؟ خیر. این حرکت را میتوانیم به عنوان حرکتی شتابدار در نظر بگیریم. به نقطه حساسی رسیدهایم. به این جمله دقت کنید، اندازه سرعت ثابت است، اما جهت آن تغییر میکند. آیا تغییر جهت سرعت به ما شتاب میدهد؟ بله. درک این موضوع کمی سخت و پیچیده است. به تعریف شتاب دقت کنید: به تغییرات سرعت نسبت به زمان شتاب گفته میشود.
منظور از تغییرات سرعت، تنها تغییر اندازه سرعت نیست، بلکه تغییر جهت سرعت نیز میتواند شتاب ایجاد کند. همانطور که گفتیم، سرعت جسم در حرکت دایرهای، بر دایره مماس است. شتاب در چه جهتی قرار دارد؟ برای پیدا کردن جهت شتاب، ابتدا نیروی وارد شده بر جسم را بررسی میکنیم. با یافتن جهت نیرو، به راحتی میتوانیم جهت شتاب را بهدست آوریم. برای یافتن جهت نیرو، بار دیگر به مثال چرخش توپ بسته شده به نخ برمیگردیم. نیروی وارد شده بر توپ در این حالت، نیروی کشش طناب، متصل به آن است. جهت این نیرو به کدام سمت است؟ نیرو در راستای طناب و جهت آن به سمت مرکز دایره است. به این نیرو، نیروی مرکزگرا گفته میشود.
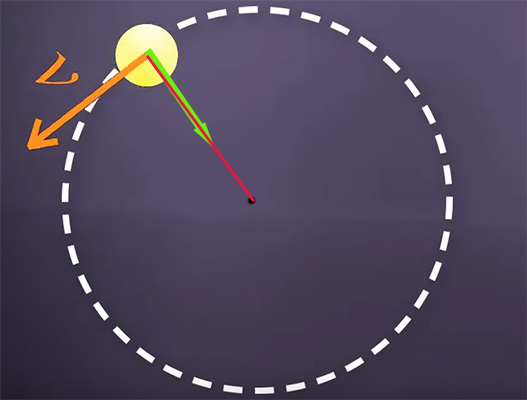
به کلمه مرکزگرا دقت کنید. نیروی مرکزگرا، نیرویی است که به سمت مرکز تمایل دارد و جهت آن همراه به سمت مرکز دایره است. به حرکت زمین به دور خورشید دقت کنید. نیروی گرانشی خورشید سبب حرکت یکنواخت زمین روی مسیری به شکل دایره میشود. این نیروی گرانشی، نیروی مرکزگرا و جهت آن به سمت خورشید (مرکز) است. اگر نیروی گرانشی خورشید بر زمین وارد نمیشد، چه اتفاقی رخ میداد؟ زمین در فضا رها میشد. این حالت مشابه زمانی است که توپ متصل به نخ را پس از چند دور چرخش، رها میکنید. توپ و نخ پس از رها شدن، در هوا شروع به حرکت میکنند. فراموش نکنید که نیروی مرکزگرا ستون حرکت دایرهای یکنواخت است.
بر طبق قانون دوم نیوتن، نیرو و شتاب با یکدیگر رابطه خطی دارند و جهت هر دو یکسان است. از آنجا که جهت نیروی مرکزگرا به سمت مرکز دایره قرار میگیرد، جهت بردار شتاب نیز به سمت مرکز قرار دارد. به این شتاب، شتاب مرکزگرا گفته میشود. در حرکت دایرهای یکنواخت، بردارهای شتاب و سرعت، همواره بر یکدیگر عمود هستند. به این نکته توجه داشته باشید که از چرخش زمین به دور خورشید به عنوان مثالی برای حرکت دایرهای یکنواخت استفاده کردیم، اما در واقعیت زمین روی مسیری به شکل بیضی به دور خورشید میچرخد و حرکت آن را نمیتوانیم به عنوان حرکت دایرهای یکنواخت در نظر بگیریم.
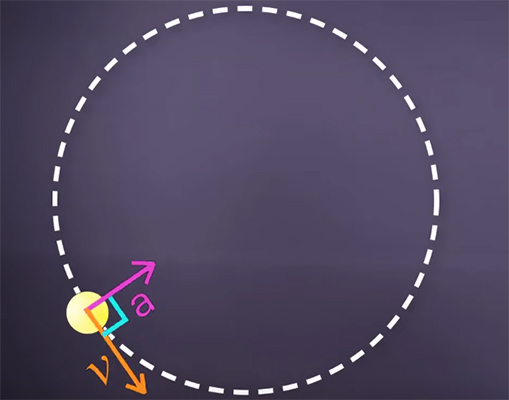
حل تمرین حرکت دایره ای یکنواخت
در این بخش با حرکت دایرهای یکنواخت آشنا شدیم. در ادامه، چند تمرین را در این رابطه با یکدیگر حل میکنیم.
تمرین ۱
کودکی یویویی به جرم ۰٫۰۱ کیلوگرم را در مسیری دایرهای و عمود بر زمین میچرخاند. یویو در جهت ساعتگرد و با تندی ثابت ۲ متر بر ثانیه میچرخد. سرعت یویو در کف مسیر دایرهای چه مقدار است و در چه جهتی قرار دارد؟

در حرکت دایرهای یکنواخت، سرعت همواره بر دایره مماس است. بنابراین، گرچه تندی حرکت ثابت است، جهت سرعت به طور پیوسته تغییر میکند. دایره نشان داده شده در تصویر زیر، مسیر یویو را نشان میدهد. از آنجا که یویو در جهت عقربههای ساعت حرکت میکند، جهت سرعت در کف دایره، به سمت چپ خواهد بود. همچنین، مقدار سرعت همواره ثابت و برابر تندی، یعنی ۲ متر بر ثانیه است.
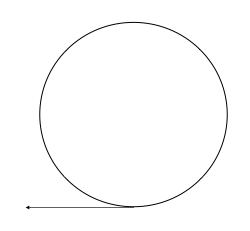
تمرین ۲
اتومبیلی با سرعت ۶۰ کیلومتر بر ساعت در اتوبان حرکت میکند. راننده با نزدیک شدن به خروجی اتوبان، ترمز میکند و سرعت اتومبیل به ۳۵ کیلومتر بر ساعت کاهش مییابد. خروجی اتوبان، مسیری دایرهای با شعاع مشخص است. راننده برای عبور از این مسیر، با همان سرعت ۳۵ کیلومتر بر ساعت به حرکت خود ادامه میدهد. چه نیرویی اتومبیل را در مسیر دایرهای نگه میدارد؟
نیروی وزن اتومبیل
نیروی عمودی سطح
نیروی مرکزگرا
پاسخ صحیح، نیروی مرکزگرا است.
تمرین ۳
توپِ متصل به نخی روی مسیر دایرهای عمودی و در جهت مخالف عقربههای ساعت حرکت میکند. هنگامیکه توپ در بالاترین نقطه در مسیر خود قرار دارد (بالای دایره)، نخ پاره میشود. توپ بلافاصله پس از بریده شدن نخ در چه جهتی حرکت میکند؟
در حرکت دایرهای یکنواخت، سرعت بر دایره مماس است. از آنجا که توپ، خلاف جهت عقربههای ساعت حرکت میکند، جهت بردار سرعت در بالاترین نقطه روی دایره به سمت چپ است. بنابراین، توپ بالافاصله پس از بریدن نخ به سمت چپ حرکت میکند.
جمعبندی
در این مطلب از مجله فرادرس، به بررسی حرکت یکنواخت و حل چند مثال در این زمینه پرداختیم. در حرکت یکنواخت، سرعت جسم در طول زمان ثابت میماند. به عبارت دیگر، جسم در فاصلههای زمانی مساوی، مسافتهای مساوی را طی میکند. همچنین، در حرکت یکنواخت جسم ممکن است روی خط مستقیم یا مسیری به شکل دایره حرکت کند.
source