در دنیای فیزیک، با دو نوع کمیت با نام‌های کمیت‌های برداری و کمیت‌های نرده‌ای یا اسکالر سر و کار داریم. کمیت‌های نرده‌ای، مانند جرم، دما و زمان، فقط اندازه دارند. اما کمیت‌های برداری، مانند نیرو و سرعت، علاوه بر اندازه، جهت نیز دارند. به عبارت دیگر، برای بیان کامل کمیت برداری، باید هم مقدار و هم جهت آن را مشخص کنیم.  کمیت‌های برداری در بسیاری از شاخه‌های علم، مانند فیزیک، مهندسی و نجوم، نقش مهمی دارند. به عنوان مثال، برای محاسبه مسیر حرکت موشک یا برای تعیین نیروی وارد شده بر جسم، به کمیت‌های برداری نیاز داریم. در این مطلب از مجله فرادرس، ابتدا به پرسش کمیت برداری چیست به زبان ساده پاسخ می‌دهیم. سپس در مورد تفاوت کمیت‌های برداری و اسکالر صحبت می‌کنیم. در ادامه،‌ با جمع و تفریق کمیت‌های برداری با یکدیگر با استفاده از قانون مثلث، متوازی‌الاضلاع و تجزیه‌ بردارها به همراه حل مثال آشنا می‌شویم. در پایان، دو ضرب برداری نقطه‌ای و خارجی را توضیح می‌دهیم.

کمیت برداری چیست؟

به کمیت‌هایی که اندازه و جهت دارند، کمیت برداری گفته می‌شود. برای شناخت کمیت‌ برداری، باید اندازه و جهت آن را بدانیم و تنها با دانستن اندازه یا جهت، نمی‌توانیم کمیت‌های برداری را توصیف کنیم. به عنوان مثال، اگر بخواهیم به خانه دوستی برویم باید بدانیم خانه او در چه فاصله‌ای نسبت به ما قرار گرفته است و در چه جهتی باید حرکت کنیم. یکی از مهم‌ترین ویژگی‌های بردارها آن است که نسبت به دستگاه مختصات، ثابت باقی می‌مانند. برای یادگیری بیشتر در مورد کمیت‌های برداری می‌توانید فیلم آموزش ریاضی هشتم فرادرس که لینک آن در ادامه آورده شده است را مشاهده کنید.

برای درک بهتر این موضوع، مثال ساده‌ای را با یکدیگر بررسی می‌کنیم. فرض کنید علی و سعید به گردش رفته‌اند و برای یافتن مکانی مناسب برای اتراق، چادر مسافرتی خود را جابجا می‌کنند. همان‌طور که در تصویر زیر مشاهده می‌کنید، علی و سعید، روبروی یکدیگر و در دو سوی مخالف چادر، ایستاده‌اند.

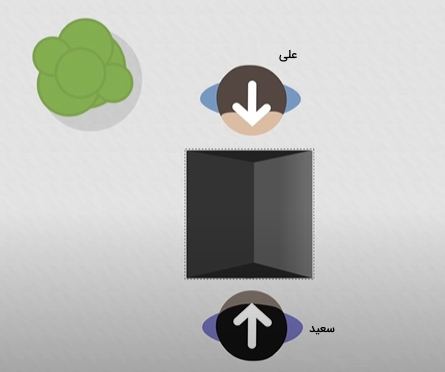
در ادامه، سعید دو قدم به سمت راست و سه قدم به سمت بالا حرکت می‌کند.

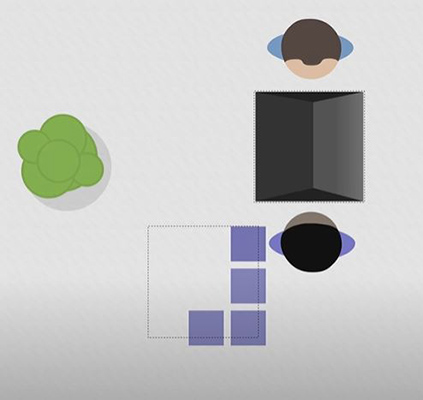
در مقابل، علی دو قدم به سمت چپ و سه قدم به سمت پایین حرکت می‌کند.

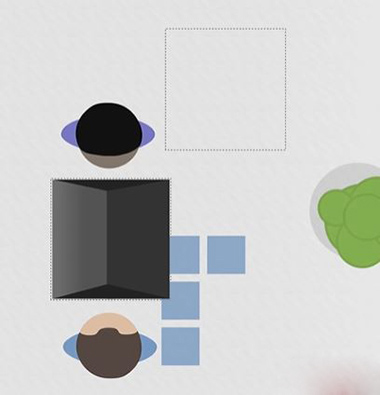
در نگاه نخست این‌گونه به نظر می‌رسد که علی و سعید حرکت‌های متفاوتی انجام داده‌اند، اما هر دوی آن‌ها مسافتِ برابری را در جهت یکسان، طی کرده‌اند. از آنجا که علی و سعید، مسافتِ برابری را در جهت یکسان طی کرده‌اند، بردارهای متصل شده به آن‌ها نیز با یکدیگر برابر هستند. در نتیجه، اندازه و جهت بردار علی و سعید، مستقل از جهتِ ایستادن آن‌ها یا دستگاه مختصاتی است که در آن قرار گرفته‌اند.

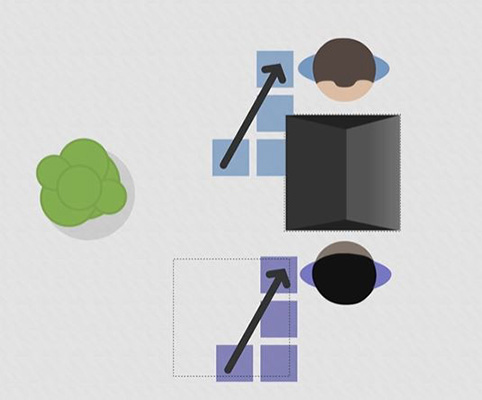
نمایش کمیت برداری در دستگاه مختصات دکارتی

در بخش قبل فهمیدیم کمیت برداری چیست و چه ویژگی‌هایی دارد. بردارها را می‌توانیم در دستگاه مختصات دکارتی نشان دهیم. دستگاه مختصات دکارتی دوبعدی از دو محور عمود بر هم به نام‌های $$x$$ و $$y$$ تشکیل شده است که به صورت عمود بر یکدیگر قرار گرفته‌اند. محل تقاطع این دو محور، مبدا مختصات نام دارد. هر بردار را می‌توانیم در دستگاه مختصات دکارتی نشان دهیم. برای نشان دادن بردار در دستگاه مختصات دکارتی باید اندازه و جهت آن را بدانیم. بردار جابجایی علی و سعید در تصویر فوق نشان داده شده است. این دو بردار به صورت پیکانی با جهتی مشخص نشان داده شده‌اند. برای نشان دادن هر بردار در دستگاه مختصات دکارتی ابتدا باید به دو نکته در مورد آن‌ها توجه کنیم:

1. اندازه بردار با اندازه پیکان برابر است.
2. ابتدای پیکان، نقطه ابتدای بردار و انتهای پیکان، نقطه انتهای بردار را نشان می‌دهد.

برای نشان دادن بردار جابجایی علی و سعید روی دستگاه مختصات دکارتی، مکان اولیه چادر مسافرتی را به عنوان مبدا مختصات (نقطه $$o$$) در نظر می‌گیریم. همچنین، مکان چادر پس از جابجایی را با نقطه B نشان می‌دهیم. این دو نقطه به صورت نشان داده شده در تصویر زیر، در دستگاه مختصات دکارتی نشان داده شده‌اند.

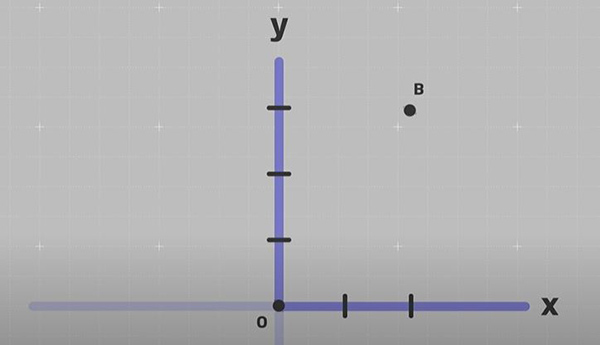
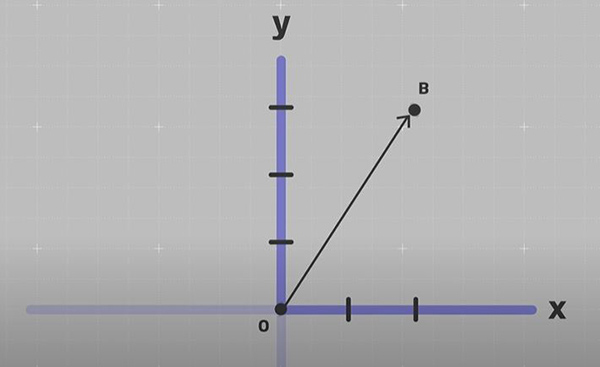
در ادامه، بردارِ جابجایی را رسم و برای رسم آن، پیکانی از $$O$$ به B رسم می‌کنیم. پیکان رسم شده از $$O$$ به B، برداری است که نقطه $$O$$ یا نقطه آغاز را به نقطه B یا نقطه پایان وصل کرده است. تصویر این بردار را می‌توانیم در امتداد محورهای $$x$$ و $$y$$ به‌دست آوریم.

تا اینجا می‌دانیم کمیت برداری چیست. کمیت‌های برداری، اندازه و جهت دارند. آیا تمام کمیت‌های فیزیکی، برداری هستند؟ خیر. برخی کمیت‌ها در فیزیک، اسکالر یا نرده‌ای هستند و تنها اندازه دارند. در ادامه، تفاوت کمیت‌های برداری و اسکالر را با یکدیگر بررسی می‌کنیم.

تفاوت کمیت اسکالر و کمیت برداری چیست؟

در قسمت قبل با تعریف کمیت برداری آشنا شدیم. کمیت‌های برداری اندازه و جهت، اما کمیت‌های اسکالر یا نرد‌ه‌ای، تنها اندازه دارند. فرض کنید آجری روی زمین قرار دارد. آجر را از روی زمین برمی‌داریم و آن را در فاصله دورتری از مکان اولیه‌اش قرار می‌دهیم. با استفاده از خط‌کش فاصله دو نقطه یک و دو را اندازه می‌گیریم. فرض کنید، فاصله این دو نقطه، برابر پنج سانتی‌متر است. برای یادگیری بیشتر در مورد کمیت‌های برداری و تفاوت آن با کمیت‌های اسکالر می‌توانید فیلم آموزش علوم تجربی پایه نهم بخش فیزیک فرادرس که لینک آن در ادامه آورده شده است را مشاهده کنید.

فاصله بین این دو نقطه را به عنوان کمیت برداری در نظر می‌گیریم یا به عنوان کمیت اسکالر؟ اگر بگوییم فاصله بین دو نقطه یک و دو برابر پنج سانتی‌متر است، تنها می‌دانیم دو نقطه در چه فاصله‌ای از یکدیگر قرار گرفته‌اند و هیچ اطلاعاتی در مورد جهت حرکت آجر نداریم.

در فیزیک دو کمیت به نام‌های جابجایی و مسافت داریم. به مجموع طول طی شده توسط جسم بدون در نظر گرفتن جهت حرکت و نقطه‌های شروع و پایان، مسافتِ طی شده توسط آن جسم گفته می‌شود. در نتیجه، مسافت طی شده توسط جسم کمیتی نرده‌ای است. در مقابل، جابجایی کمیتی برداری و به طور کامل وابسته به جهت حرکت است. مانند هر برداری، جابجایی اندازه و جهت دارد و نقاط ابتدایی و انتهایی را به هم وصل می‌کند. بنابراین، با توجه به تعریف‌های جابجایی و مسافت، اگر بگوییم آجر، ۵ متر حرکت کرده است و به جهت حرکت آن اشاره‌ای نکنیم، در مورد مسافت طی شده توسط آجر صحبت می‌کنیم.

اما اگر بگوییم آجر به اندازه ۵ متر به سمت راست حرکت کرده است، به جابجایی آن اشاره می‌کنیم. دو کمیت دیگر به نام‌های تندی و سرعت در فیزیک وجود دارند. نسبت مسافت طی شده توسط جسم به زمان لازم برای طی آن مسافت، تندی گفته می‌شود. تندی، کمیتی نرده‌ای و تنها دارای اندازه است. سرعت نیز به صورت نسبت جابجایی جسم به زمان لازم برای آن جابجایی، تعریف می‌شود. سرعت کمیتی برداری و علاوه بر اندازه، دارای جهت نیز است. فرض کنید، آجر در مدت زمان ۲ ثانیه به اندازه ۵ متر حرکت می‌کند. تندی آجر برابر است با:

$$Speed = frac { 5 m } { 2 s } = 2.5 frac { m} { s } $$

تندی، جهت ندارد. از آنجا که جابجایی و مسافت با یکدیگر برابر هستند، اندازه سرعت و تندی نیز مساوی یکدیگر خواهند بود. بنابراین، اندازه سرعت نیز برابر ۲٫۵ متر بر ثانیه است. اما نباید فراموش کنیم سرعت کمیتی برداری است و علاوه بر اندازه، جهت نیز دارد. آجر به سمت راست جابجا شده است، بنابراین جهت بردار سرعت نیز به سمت راست خواهد بود. کمیتی برداری مانند سرعت را به صورت $$overrightarrow{ v } $$ نشان می‌دهیم. توجه به این نکته مهم است که کمیت‌های برداری ممکن است مثبت یا منفی باشند. برای تعیین علامت کمیت‌های برداری، مراحل زیر را طی می‌کنیم:

• جهتی را به صورت قراردادی به عنوان جهت مثبت انتخاب می‌کنیم.
• اگر جهت کمیت برداری در جهت قراردادی مثبت باشد، آن را مثبت و اگر در خلاف جهت قراردادی باشد، آن را منفی در نظر می‌گیریم.

تا اینجا می‌دانیم تفاوت کمیت اسکالر و کمیت برداری چیست. در ادامه، برای درک بهتر این دو کمیت و تفاوت‌های آن‌ها مثالی را با یکدیگر حل می‌کنیم.

مثال محاسبه مسافت و جابجایی

جسمی روی محور نشان داده شده در تصویر زیر از نقطه A به نقطه B و سپس به نقطه C می‌رود. در ادامه، جسم در امتداد محور به نقطه B و در پایان، به نقطه C برمی‌گردد.

1. مسافت طی شده توسط جسم را به‌دست آورید.
2. اندازه و جهت جابجایی طی شده توسط جسم را به‌دست آورید.

پاسخ

قبل از حل این مثال، آن را با دقت مرور و نکته‌های مهم را یادداشت می‌کنیم. جسم ابتدا در نقطه A قرار دارد. همان‌طور که در تصویر فوق نشان داده شده، مکان نقطه A برابر صفر است. حرکت جسم در ادامه و به ترتیب برابر است با:

1. جسم از A به B می‌رود. فاصله A تا B برابر ۵ کیلومتر است.
2. جسم از B به C می‌رود. فاصله B تا C برابر ۴ کیلومتر است.
3. جسم از C به B می‌‌رود، یعنی ۴ کیلومتر به سمت چپ حرکت کرده است.
4. در پایان، جسم از B به C می‌رود.

در قسمت یک می‌خواهیم مسافت طی شده توسط جسم را به‌دست آوریم. مسافت، کمیتی نرده‌ای است. همان‌طور که اشاره شد به مجموع طول طی شده توسط جسم، بدون در نظر گرفتن جهت حرکت و نقطه‌های شروع و پایان، مسافت گفته می‌شود. بنابراین، مسافت کل طی شده توسط جسم برابر است با:

$$ AB+BC+CB+BC = 5 + 4 + 4 + 4 = 17 km $$

شاید با خود بگویید، CB برابر ۴- است. فراموش نکنید که به هنگام محاسبه مسافت، نقطه‌های ابتدا و انتها و جهت حرکت مهم نیستند، بلکه مسیر طی شده مهم است. در ادامه و در قسمت دو، جابجایی جسم را به‌دست می‌آوریم. جابجایی کمیتی برداری و به طور کامل وابسته به جهت حرکت است. جابجایی مانند هر برداری، اندازه و جهت دارد و نقاط ابتدایی و انتهایی را به هم وصل می‌کند. برای محاسبه جابجایی، حرکت به سمت راست را به عنوان جهت مثبت در نظر می‌گیریم. جهت حرکت جسم در هر مرحله در تصویر زیر نشان داده شده است.

در نتیجه، جابجایی جسم برابر است با:

$$overrightarrow{ AB } + overrightarrow{ BC } – overrightarrow{ CB } + overrightarrow{ BC }= 5+4-4+4= 9 km $$

جابجایی جسم برابر ۹ کیلومتر و جهت آن به سمت راست است.

پرسش: اگر مدت زمان حرکت جسم در مثال یک برابر ۳۰ دقیقه باشد، سرعت و تندی حرکت جسم چه مقدار است؟

پاسخ: برای محاسبه تندی باید مسافت طی شده را بر زمان تقسیم کنیم:

$$Speed = frac { 17 } { 0.5 h } = 34 frac { km } { h } $$

تندی، کمیتی اسکالر یا نرده‌ای است و تنها اندازه دارد. برای محاسبه سرعت، جابجایی را بر زمان داده شده تقسیم می‌کنیم:

$$Velocity = frac {  9  } { 0.5 h } = 18 frac { km } { h } $$

سرعت، کمیتی برداری است و جهت آن به سمت راست، هم‌جهت با جابجایی، است.

اکنون می‌دانیم کمیت برداری چیست و چه تفاوتی با کمیت اسکالر دارد. کمیت‌های برداری را می‌توان همانند کمیت‌های نرده‌ای (اعداد) با یکدیگر جمع، تفریق یا ضرب کرد. اما جمع، تفریق و ضرب بردارها با کمیت‌های اسکالر متفاوت است. در ادامه، با جمع، تفریق و ضرب بردارها آشنا می‌شویم.

چگونه مسائل مربوط به بردارها را به راحتی حل کنیم؟

در بخش‌های قبل فهمیدیم کمیت برداری چیست و چه تفاوتی با کمیت اسکالر دارد. به هر کمیت فیزیکی، مانند جابجایی و سرعت، که اندازه و جهت دارند،کمیت برداری گفته می‌شود. در حل بسیاری از مسائل فیزیکی، مانند مسائل مربوط به محاسبه نیروهای وارد شده بر اجسام، باید با مفهوم بردار، جمع، تفریق، ضرب و تجزیه بردارها آشنا باشیم. بنابراین، آشنایی با بردارها از اهمیت بالایی برخوردار است. در ریاضی هشتم با مفهوم بردار، نمایش آن در دستگاه مختصات دوبعدی، بردارهای واحد و جمع بردارها آشنا می‌شوید. کاربرد کمیت‌های برداری را می‌توانید در فیزیک نهم مشاهده کنید. تماشای فیلم‌های آموزشی، مانند فیلم‌های آموزشی تهیه شده در فرادرس، می‌تواند به شما برای درک بهتر بردارها و مسائل مربوط به آن‌ها کمک زیادی کند.

پس از آشنایی با مفهوم کمیت‌های برداری، مباحث پیشرفته‌تر را می‌توانید در درس فیزیک یک دانشگاهی بیاموزید. در این راستا، تماشای مجموعه فیلم‌های آموزشی فرادرس در زمینه فیزیک یک دانشگاهی به شما در یادگیری بیشتر کمیت‌های برداری و حل مسائل پیشرفته‌تر، کمک شایانی می‌کند.

تا اینجا می‌دانیم کمیت برداری چیست. کمیت‌های برداری و آشنایی با ویژگی‌های آن‌ها برای حل مسائل مختلف فیزیک، مانند مسائل مربوط به نیرو، لازم است. برای حل این مسائل باید بدانیم این بردارها چگونه با یکدیگر جمع یا از هم کم می‌شوند. در ادامه، با جمع و تفریق کمیت‌های برداری آشنا می‌شویم.

جمع و تفریق کمیت های برداری

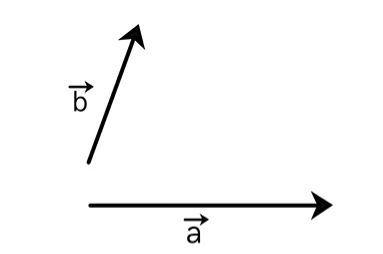
دو بردار $$overrightarrow{ a } $$ و $$overrightarrow{ b }$$ به صورت نشان داده شده در تصویر زیر در نظر بگیرید.

بردارها را به دو روش کلی می‌توان با یکدیگر جمع کرد:

1. قانون مثلث
2. قانون متوازی‌الاضلاع

در جمع بردارها مهم نیست از کدام یک از این دو قانون استفاده کنیم. نتیجه نهایی یکسان خواهد بود.

قانون متوازی الاضلاع در جمع کمیت برداری چیست؟

با استفاده از قانون متوازی‌الاضلاع، جمع دو بردار $$overrightarrow{ a } $$ و $$overrightarrow{ b }$$ را به‌دست می‌آوریم. برای انجام این کار، یکی از بردارها، به عنوان مثال بردار $$overrightarrow{ a } $$ را ثابت نگه می‌داریم و بردار $$overrightarrow{ b }$$ را بدون تغییر جهت به گونه‌ای جابجا می‌کنیم که ابتدای آن روی نقطه ابتدایی بردار $$overrightarrow{ a } $$ قرار گیرد.

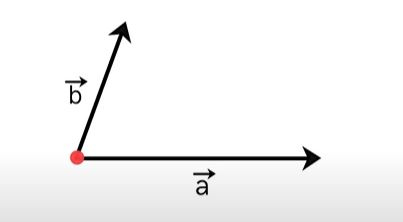
در ادامه، از انتهای بردار $$overrightarrow{ a } $$ خطی موازی بردار $$overrightarrow{ b }$$ و از انتهای بردار $$overrightarrow{ b }$$، خطی موازی بردار $$overrightarrow{ a } $$ رسم می‌کنیم. دو خط موازی یکدیگر را قطع می‌کنند و متوازی‌الاضلاعی به صورت نشان داده شده در تصویر زیر تشکیل می‌شود.

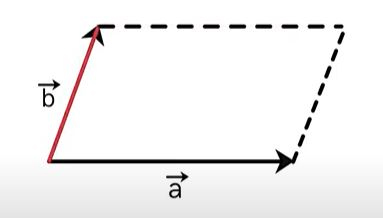
سپس، قطر OC را به صورت نشان داده شده در تصویر زیر رسم می‌کنیم. این قطر برابر جمع برداری $$overrightarrow{ a } + overrightarrow{ b }$$ است.

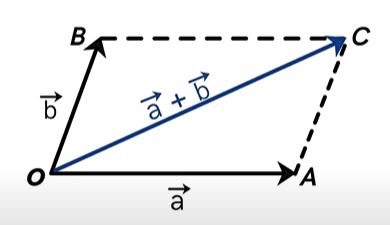
جمع برداری فوق را می‌توانیم به صورت زیر نیز بنویسیم:‌

$$overrightarrow{ OA } + overrightarrow{ OB  } = overrightarrow{ OC }$$

در ادامه، دو بردار $$overrightarrow{ a } $$ و $$overrightarrow{ b }$$ را با استفاده از قانون مثلث با یکدیگر جمع می‌کنیم.

قانون مثلث در جمع کمیت برداری چیست؟

با استفاده از قانون مثلث، جمع دو بردار $$overrightarrow{ a } $$ و $$overrightarrow{ b }$$ را به‌دست می‌آوریم. برای انجام این کار، یکی از بردارها، به عنوان مثال بردار $$overrightarrow{ a } $$ را ثابت نگه می‌داریم و بردار $$overrightarrow{ b }$$ را بدون تغییر جهت به گونه‌ای جابجا می‌کنیم که ابتدای آن روی نقطه انتهایی بردار $$overrightarrow{ a } $$ قرار گیرد.

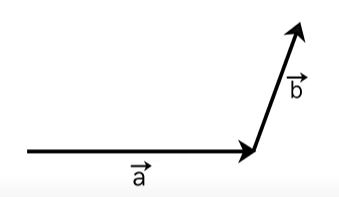
سپس، ابتدای بردار $$overrightarrow{ a } $$ را به صورت نشان داده شده در تصویر زیر به انتهای بردار $$overrightarrow{ b }$$ وصل می‌کنیم.

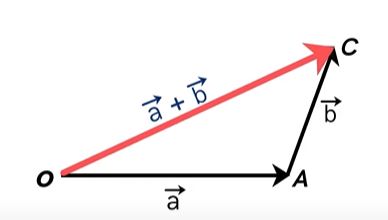
جمع برداری فوق را می‌توانیم به صورت زیر نیز بنویسیم:‌

$$overrightarrow{ OA } + overrightarrow{ AC } = overrightarrow{ OC }$$

به این نکته توجه داشته باشید که بردارهای $$overrightarrow{ OB  } $$ و $$overrightarrow{ AC }$$ با یکدیگر و در نتیجه، حاصل جمع برداری به‌دست با استفاده از قانون متوازی‌الاضلاع و قانون مثلث نیز با یکدیگر برابر هستند.

تا اینجا فهمیدیم چگونه دو کمیت برداری را با یکدیگر جمع کنیم. در ادامه، در مورد تفاضل کمیت‌های برداری صحبت می‌کنیم. تفاضل دو عدد را به راحتی می‌توانیم به‌دست آوریم. اعداد ۵ و ۲ را در نظر بگیرید. تفاضل این دو عدد به صورت $$ 5   – 2 $$ نوشته می‌شود. حاصل برابر ۳ است. حاصل $$5 + (-2 )$$ نیز برابر ۲ به‌دست می‌آید. بنابراین، تفاضل دو عدد را به صورت جمع آن‌ها نیز می‌توان نوشت. به طور مشابه، تفاضل دو بردار $$overrightarrow{ a } – overrightarrow{ b }$$ را نیز می‌توانیم به صورت $$overrightarrow{ a } + ( – overrightarrow{ b } ) $$ بنویسیم. بردارهای $$overrightarrow{ b }$$ و $$ – overrightarrow{ b }  $$ چه تفاوتی با یکدیگر دارند؟ بردار $$ – overrightarrow{ b }  $$ هم‌اندازه با بردار $$overrightarrow{ b }$$، اما جهت آن مخالف جهت بردار $$overrightarrow{ b }$$ است.

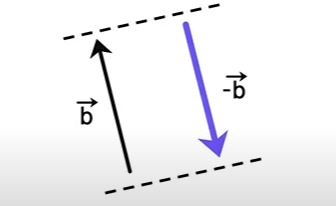
بنابراین، تفاضل دو بردار را نیز می‌توانیم با استفاده از قانون‌های مثلث و متوازی‌الاضلاع به‌دست آوریم. حاصل $$overrightarrow{ a } + ( – overrightarrow{ b } ) $$ را با استفاده از قانون مثلث محاسبه می‌کنیم. برای انجام این کار، یکی از بردارها، به عنوان مثال بردار $$overrightarrow{ a } $$ را ثابت نگه می‌داریم و بردار $$- overrightarrow{ b }$$ را بدون تغییر جهت به گونه‌ای جابجا می‌کنیم که ابتدای آن روی نقطه انتهایی بردار $$overrightarrow{ a } $$ قرار گیرد. سپس، ابتدای بردار $$overrightarrow{ a } $$ را به صورت نشان داده شده در تصویر زیر به انتهای بردار $$- overrightarrow{ b }$$ وصل می‌کنیم.

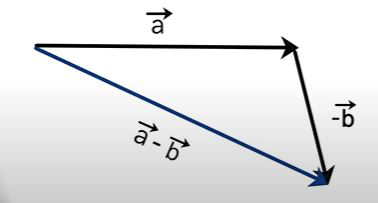
توجه به این نکته مهم است که جمع و تفریق بیش از دو بردار را نیز می‌توانیم با استفاده از این دو قانون به‌دست آوریم. همچنین، دو قانون مثلث و متوازی‌الاضلاع، تنها به ما جهت بردار حاصل را می‌دهد.برای به‌دست آوردن اندازه بردار حاصل باید از روش‌های دیگری استفاده کنیم. یکی از این روش‌های تجزیه بردار و نوشتن آن‌ها برحسب مولفه‌های یکه است. در ادامه، با تجزیه بردارها در فضای دوبعدی و سه‌بعدی و سپس محاسبه جمع و تفاضل بردارها با استفاده از این روش آشنا می‌شویم.

تجزیه کمیت برداری چیست؟

قبل از صحبت در مورد تجزیه بردارها، ابتدا در مورد دستگاه مختصات صحبت می‌کنیم. همان‌طور که در ابتدای این مطلب مشاهده کردید، بردارها را می‌توانیم در دستگاه مختصاتی به نام دستگاه مختصات دکارتی نشان دهیم. دستگاه مختصات در دو بعد از یک خط افقی، محور $$x$$، و یک خط عمودی، محور $$y$$، تشکیل شده است. هر یک از محورها به فاصله‌های مساوی تقسیم شده‌اند و هر فاصله با عددی مشخص نشان داده شده است. هر نقطه در این دستگاه مختصات، با توجه به مکان آن، با دو مولفه $$x$$ و $$y$$ نشان داده می‌شود. مختصات نقطه را چگونه به‌دست می‌آوریم. برای به‌دست آوردن مختصات هر نقطه، دو خط از نقطه مورد نظر، به صورت نشان داده شده در تصویر زیر، موازی محورهای $$x$$ و $$y$$ رسم می‌کنیم.

توجه به این نکته مهم است که برای نوشتن مختصات هر نقطه، ابتدا مختصات نقطه $$x$$ و سپس مختصات نقطه $$y$$ را می‌نویسیم. همچنین، محل تقاطع محورهای $$x$$ و $$y$$ با یکدیگر مبدا مختصات نام دارد و با $$O$$ نشان داده می‌شود. مختصات این نقطه برابر $$ ( 0 , 0 ) $$ است. بردارها با پیکان نشان داده می‌شوند و اندازه و جهتی مشخص دارند. برای به‌دست آوردن مختصات $$x$$ و $$y$$ بردار به صورت زیر عمل می‌کنیم:

• برای محاسبه مختصات $$x$$، از نقطه ابتدایی بردار شروع می‌کنیم و با توجه به جهت بردار، روی محور افقی به سمت راست یا چپ حرکت می‌کنیم. تعداد تقسیم‌بندی محور $$x$$ از نقطه ابتدایی تا نقطه انتهایی برابر مختصات $$x$$ است. اگر به سمت راست حرکت کنیم، علامت $$x$$ مثبت و اگر به سمت چپ حرکت کنیم، علامت $$x$$ منفی است.
• برای محاسبه مختصات $$y$$، از نقطه ابتدایی بردار شروع می‌کنیم و با توجه به جهت بردار، روی محور عمودی به سمت بالا یا پایین حرکت می‌کنیم. تعداد تقسیم‌بندی محور $$y$$ از نقطه ابتدایی تا نقطه انتهایی برابر مختصات $$y$$ است. اگر به سمت بالا حرکت کنیم، علامت $$y$$ مثبت و اگر به سمت پایین حرکت کنیم، علامت $$y$$ منفی است.

مختصات بردار را می‌توان به دو صورت $$(a , c ) $$ یا $$begin{bmatrix}a \c end{bmatrix}$$ نوشت. بردارها در فضای سه‌بعدی، مختصه سومی به نام z دارند و به صورت $$begin{bmatrix}a \b \ c end{bmatrix}$$ نوشته می‌شوند. محور z بر محورهای $$x$$ و $$y$$ عمود و عمود بر صفحه ساخته شده توسط این دو محور است.

بردارها را می‌توان برحسب مولفه‌های یکه نوشت. معنای این جمله چیست؟ همان‌طور که در مطالب بالا خواندیم هر بردار را می‌توانیم در دستگاه مختصات دکارتی نشان دهیم. بردارهای دوبعدی، دو مولفه در راستای محورهای $$x$$ و $$y$$ و بردارهای سه‌بعدی، سه مولفه در راستای محورهای $$x$$ و $$y$$ و $$z$$ دارند و به صورت زیر نوشته می‌شوند:

$$overrightarrow{A}= A_x overrightarrow{a _x}+ A_y overrightarrow{a _y} \ overrightarrow{A}= A_x overrightarrow{a _x}+ A_y overrightarrow{a _y}+ A_z overrightarrow{a _ z}$$

$$A_x$$ و $$A_y$$ و $$A_z$$ به ترتیب مولفه‌های بردار $$overrightarrow{A}$$ در راستای محورهای $$x$$ و $$y$$ و $$z$$ هستند. همچنین، بردارهای $$overrightarrow{a _x} $$ و $$overrightarrow{a _y} $$ و $$overrightarrow{a _z} $$ را به عنوان بردارهای یکه در راستای محورهای $$x$$ و $$y$$ و $$z$$ در نظر می‌گیریم. بردار یکه، برداری با اندازه واحد است که برای نشان دادن جهت مشخصی در فضا استفاده می‌شود و بردارهای دیگر را می‌توان به صورت ضریبی از آن نوشت. به عنوان مثال بردار یکه $$overrightarrow{a _x} $$، برداری واحد در راستای محور $$x $$ است و از آن برای نوشتن بردار $$overrightarrow{A}$$ در راستای محور $$x$$ استفاده می‌شود. توجه به این نکته مهم است که بردارهای $$overrightarrow{a _x} $$ و $$overrightarrow{a _y} $$ و $$overrightarrow{a _z} $$ را می‌توانیم به صورت زیر نیز نشان بنویسیم:

$$overrightarrow{a _x}= widehat{i} \ overrightarrow{a _y}= widehat{j} \ overrightarrow{a _z}= widehat {k}$$

سوال مهمی که ممکن است مطرح شود آن است که چگونه می‌توانیم بردارها را در دو و سه بعد برحسب مولفه‌های آن‌ها در راستای محورهای مختصات بنویسیم. برای انجام این کار باید تصویر بردار روی محورهای مختصات را داشته باشیم. به بیان ساده‌تر، باید بردار را به مولفه‌های سازنده آن در راستای هر محور تجزیه کنیم.

چگونه کمیت برداری را به مولفه های سازنده آن در دو بعد تجزیه کنیم؟

فرض کنید بردار دلخواهی به نام $$overrightarrow{A}$$ داریم که به صورت نشان داده شده در تصویر زیر در دستگاه مختصات دوبعدی رسم شده است. زاویه این بردار با جهت مثبت محور $$x $$ برابر $$theta $$ است. برای تجزیه این بردار به مولفه‌های سازنده‌اش، مرحله‌های زیر را به ترتیب طی می‌کنیم.

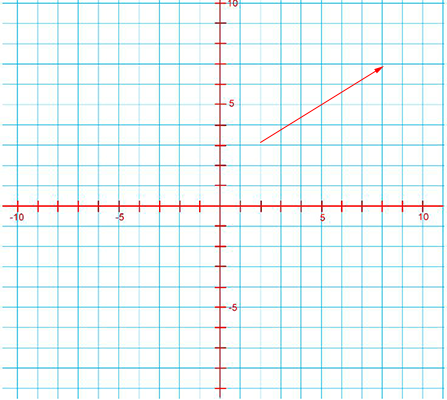
مرحله اول

ابتدا بردار $$overrightarrow{A}$$ را از مبدا مختصات رسم می‌کنیم. برای انجام این کار بردار $$overrightarrow{ A }$$ را بدون تغییر جهت به گونه‌ای جابجا می‌کنیم که ابتدای آن روی مبدا مختصات قرار گیرد.

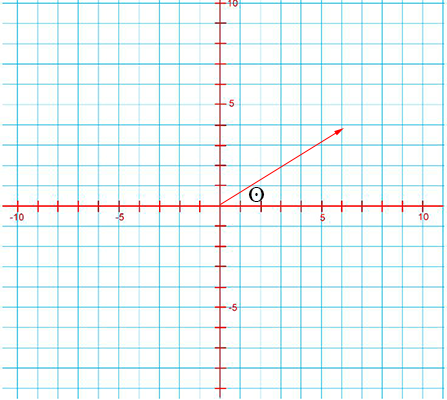
مرحله دوم

از انتهای بردار، خطی موازی محور عمودی رسم می‌کنیم و آن را تا جایی ادامه می‌دهیم که محور افقی را قطع کند. محل تقاطع با دایره قرمز‌رنگ نشان داده شده است. از مبدا مختصات، برداری را تا این نقطه رسم می‌کنیم و آن را $$overrightarrow{A _ x } $$ می‌نامیم.

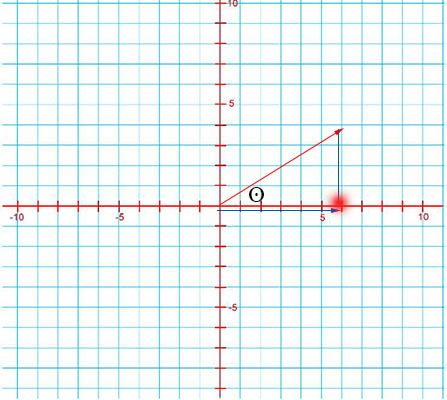
بردار $$overrightarrow{A _ y } $$ را می‌توانیم به صورت زیر بنویسیم:

$$overrightarrow{A _y }= A_y overrightarrow{a _y}
$$

مولفه $$A_y$$ تصویر بردار $$overrightarrow{A}$$ در راستای محور $$y$$ است و به صورت زیر نوشته می‌شود:

$$A_x = A cos theta $$

در رابطه فوق:

• A اندازه بردار $$overrightarrow{A}$$ است.
• $$theta$$ زاویه بردار $$overrightarrow{A}$$ با جهت مثبت محور $$x$$ است.

مرحله سوم

از انتهای بردار، خطی موازی محور افقی رسم می‌کنیم و آن را تا جایی ادامه می‌دهیم که محور عمودی را قطع کند. محل تقاطع با دایره آبی‌رنگ نشان داده شده است. از مبدا مختصات، برداری را تا این نقطه رسم می‌کنیم و آن را $$overrightarrow{A _ y } $$ می‌نامیم.

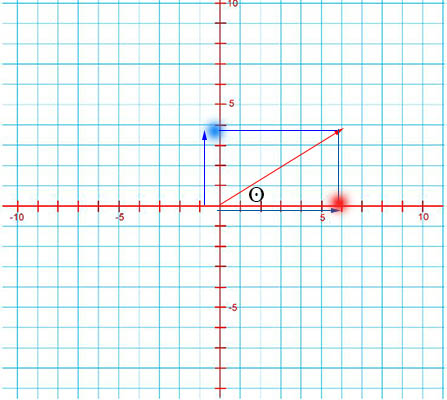
بردار $$overrightarrow{A _ x } $$ را می‌توانیم به صورت زیر بنویسیم:

$$overrightarrow{A _ x }= A_x overrightarrow{a _x}
$$

مولفه $$A_x$$ تصویر بردار $$overrightarrow{A}$$ در راستای محور $$x$$ است و به صورت زیر نوشته می‌شود:

$$A_x = A sin theta $$

در رابطه فوق:

• A اندازه بردار $$overrightarrow{A}$$ است.
• $$theta$$ زاویه بردار $$overrightarrow{A}$$ با جهت مثبت محور $$x$$ است.

مرحله چهارم

بردار $$overrightarrow{A}$$ را برحسب دو مولفه می‌توان به صورت زیر نوشت:

$$overrightarrow{A }= A cos theta widehat{i} + A sin theta widehat{ j } $$

شاید از خود بپرسید تجزیه بردار در سه‌ بعد به چه صورت انجام می‌شود. در ادامه، با تجزیه برداری در سه بعد آشنا می‌شوید.

چگونه کمیت برداری را به مولفه های سازنده آن در سه بعد تجزیه کنیم؟

فرض کنید بردار دلخواهی به نام $$overrightarrow{r}$$ داریم که به صورت نشان داده شده در تصویر زیر در دستگاه مختصات سه‌بعدی رسم شده است. زاویه این بردار با صفحه $$ xy $$ برابر $$theta $$ و با جهت مثبت محور $$z $$ برابر $$phi$$ است. برای تجزیه این بردار به مولفه‌های سازنده‌اش، مرحله‌های زیر را به ترتیب طی می‌کنیم.

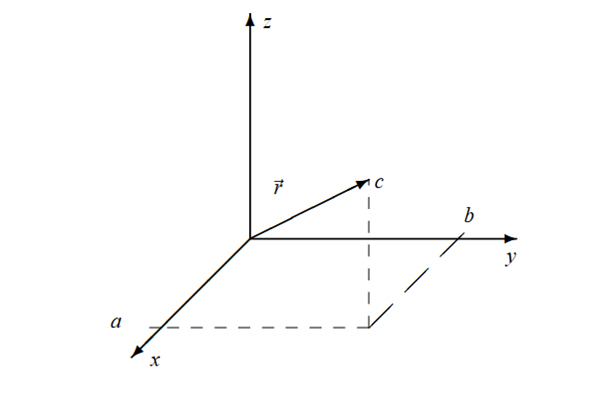
مرحله اول

ابتدا تصویر بردار $$overrightarrow{r}$$ را در صفحه $$xy$$ رسم می‌کنیم. برای انجام این کار، از انتهای بردار $$overrightarrow{r}$$ خطی موازی محور عمودی $$z$$ رسم می‌کنیم و آن را تا جایی ادامه می‌دهیم که صفحه $$xy$$ را قطع کند. محل تقاطع با دایره قرمز‌رنگ نشان داده شده است. از مبدا مختصات، برداری را تا این نقطه رسم می‌کنیم و آن را $$overrightarrow{r _  {x y } } $$ می‌نامیم.

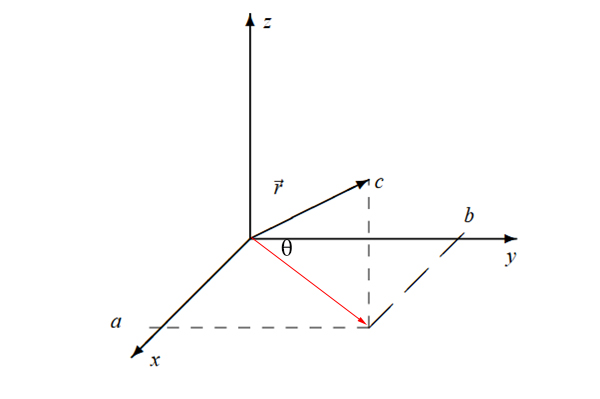
تصویر بردار $$overrightarrow{ r  } $$ روی صفحه $$xy$$ را می‌توانیم به صورت زیر بنویسیم:

$$ r _ { x y } = r cos theta $$

مرحله دوم

تصویر بردار $$overrightarrow{r _  {x y } } $$ را در راستای محورهای $$x $$ و $$y $$ به‌دست می‌آوریم. فرض کنید زاویه بردار $$overrightarrow{r _  {x y } } $$ با محور $$x$$ برابر $$theta_1 $$ است. برای انجام این کار از انتهای این بردار، خطی موازی محور $$y$$ رسم می‌کنیم و آن را تا جایی ادامه می‌دهیم که محور $$x $$ را قطع کند. محل تقاطع با دایره قرمز‌رنگ نشان داده شده است. از مبدا مختصات، برداری را تا این نقطه رسم می‌کنیم و آن را $$overrightarrow{ r _ x } $$ می‌نامیم.

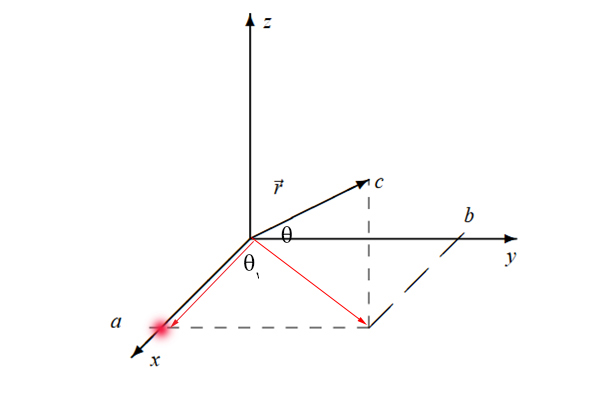
بردار $$overrightarrow{r _ x} $$ را می‌توانیم به صورت زیر بنویسیم:

$$overrightarrow{ r_ x }= r_ { xy } cos theta_1 = r cos thetacos theta_1 $$

مرحله سوم

در ادامه، تصویر بردار $$overrightarrow{r _  {x y } } $$ را در راستای محور $$y $$ به‌دست می‌آوریم. برای انجام این کار از انتهای این بردار، خطی موازی محور $$x$$ رسم می‌کنیم و آن را تا جایی ادامه می‌دهیم که محور $$ y $$ را قطع کند. محل تقاطع با دایره آبی‌رنگ نشان داده شده است. از مبدا مختصات، برداری را تا این نقطه رسم می‌کنیم و آن را $$overrightarrow{ r _ y } $$ می‌نامیم.

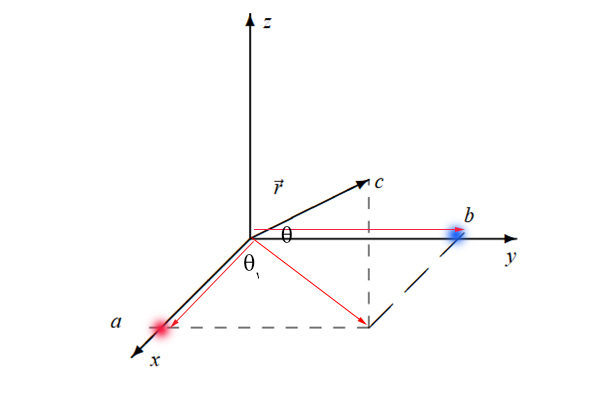
بردار $$overrightarrow{r _ y} $$ را می‌توانیم به صورت زیر بنویسیم:

$$overrightarrow{ r_ y }= r_ { xy } cos theta_1 = r cos theta sin theta_1 $$

مرحله چهارم

در پایان، تصویر بردار $$overrightarrow{ r } $$ را در راستای محور $$ z $$ به‌دست می‌آوریم. برای انجام این کار از انتهای این بردار، خطی موازی بردار $$overrightarrow{r _  {x y } } $$ رسم می‌کنیم و آن را تا جایی ادامه می‌دهیم که محور $$ z $$ را قطع کند. محل تقاطع با دایره سبزرنگ نشان داده شده است. از مبدا مختصات، برداری را تا این نقطه رسم می‌کنیم و آن را $$overrightarrow{ r _ z } $$ می‌نامیم.

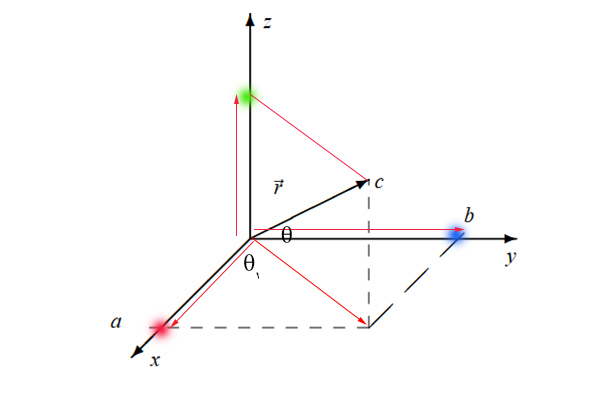
تصویر بردار $$overrightarrow{ r  } $$ روی محور $$z$$ را می‌توانیم به صورت زیر بنویسیم:

$$ r _ { z } = r sin theta $$

تا اینجا می‌دانیم کمیت برداری چیست و چگونه آن را در راستای محورهای مختصات تجزیه کنیم. برای جمع دو یا بیش از دو بردار با یکدیگر، می‌توانیم به راحتی آن‌ها را در راستای محورهای مختصات تجزیه کنیم. سپس، مولفه‌ها در راستای هر محور را مشابه کمیت‌های اسکالر با یکدیگر جمع یا از یکدیگر کم کنیم. برای درک بهتر این موضوع چند مثال را با یکدیگر حل می‌کنیم.

مثال ۱

بردار $$overrightarrow{a}$$ به صورت $$overrightarrow{a} = widehat{i } – 2 widehat{j} $$ داده شده است. کدام‌یک از گزینه‌های زیر اندازه این بردار را به‌ درستی نشان می‌دهد؟

مشاهده جواب

اگر برداری به صورت $$overrightarrow{a} = a_ x widehat{i } +a _ y widehat{j} $$ داده شده باشد، اندازه آن با استفاده از رابطه زیر به‌دست می‌آید:

$$mid overrightarrow{a} mid = sqrt { a_ x ^ 2 + a_ y ^2 } $$

از آنجا که مقدارهای $$a_x $$ و $$a_y $$ به ترتیب برابر یک و ۲- است، اندازه بردار $$overrightarrow{a}$$ برابر است با: 

$$mid overrightarrow{a} mid = sqrt { a_ x ^ 2 + a_ y ^2 } \ sqrt ( 1)^ 2 + (-2 ) ^ 2 = sqrt { 5 } $$

 مثال ۲

مردی برای خرید از فروشگاهی در نزدیکی خانه خود، باید ۲۰ متر به سمت شمال و سپس ۱۲ متر به سمت شرق حرکت کند. جابجایی او چه مقدار است؟ 

مشاهده جواب

مسیر حرکت مرد در تصویر زیر با استفاده از دو بردار عمور بر یکدیگر نشان داده شده است. 

همان‌طور که در مطالب بالا فهمیدیم، جابجایی کمیتی برداری است. برای نشان جهت این بردار باید نقطه شروع حرکت (ابتدای بردار ۲۰ متری) را به انتهای مسیر (انتهای بردار ۱۲ متری) وصل کنیم. 

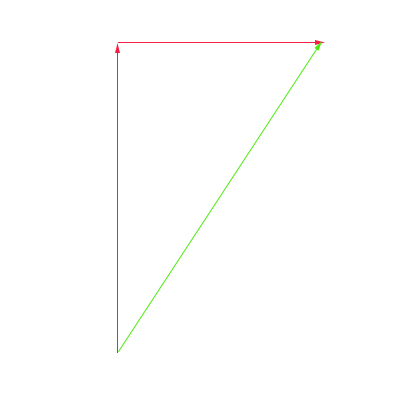
تصویر فوق، جمع دو بردار با استفاده از قانون مثلث را نشان می‌دهد. برای به‌دست آوردن اندازه بردار جابجایی از رابطه فیثاغورت استفاده می‌کنیم. چرا؟ زیرا بردارهای ۱۲ و ۲۰ متر بر یکدیگر عمود و دو ضلع مثلث قائم‌الزاویه‌ای را تشکیل می‌دهند که بردار جابجایی وتر آن است. در نتیجه اندازه بردار جابجایی برابر است با:

$$Displacement = sqrt { ( 20 ^ 2 ) + ( 12 ^ 2 )} = 23.3 m$$

مثال ۳

هواپیمایی با زاویه ۴۰ درجه بالای خط افق، با تندی ۳۰۰ کیلومتر بر ساعت به سمت غرب حرکت می‌کند. سرعت هواپیما در راستای شمال چه مقدار است؟

۲۲۹٫۸ کیلومتر بر ساعت

۱۹۲٫۸ کیلومتر بر ساعت

۱۸۸ کیلومتر بر ساعت

۱۰۸ کیلومتر بر ساعت

مشاهده جواب

بهترین راه برای حل چنین مثال‌هایی آن است که ابتدا آن‌ها را به صورت تصویری رسم کنیم. بر طبق صورت سوال، هواپیما با سرعت ۳۰۰ کیلومتر بر ساعت و با زاویه ۴۰ درجه بالای خط افق به سمت غرب حرکت می‌کند. در نتیجه، برای درک بهتر این مثال ابتدا خطی افقی رسم، سپس، بردار سرعت را به گونه‌ای رسم می‌کنیم که جهت آن به سمت غرب باشد و با خط افقی زاویه ۴۰ درجه بسازد. 

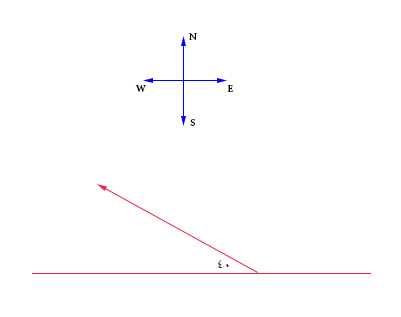
برای آن‌که بدانیم هواپیما با چه سرعتی به سمت شمال حرکت می‌کند، باید اندازه بردار آبی‌رنگ نشان داده شده در تصویر زیر را به‌دست آوریم.

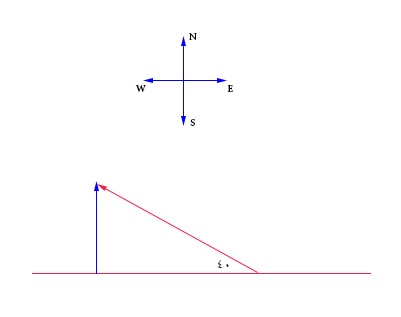
بردار آبی‌رنگ، تصویر بردار سرعت در راستای محور عمودی است (تجزیه بردارهای دوبعدی). بنابراین، اندازه آن برابر است با:

$$v_ N = 300 sin 40 = 192.8 frac { km } { h } $$

مثال ۴

فردی ۶ کیلومتر به سمت شرق و ۱۳ کیلومتر به سمت جنوب حرکت می‌کند. این فرد چند کیلومتر جابجا شده است؟

مشاهده جواب

در این پرسش می‌خواهیم جابجایی فرد را به‌دست آوریم. به یاد داشته باشید که جابجایی، برخلاف مسافت، کمیتی برداری و دارای اندازه و جهت است. فرد ۶ کیلومتر به سمت شرق و ۱۳ کیلومتر به سمت جنوب حرکت می‌کند. مسیر حرکت او در تصویر زیر نشان داده شده است.

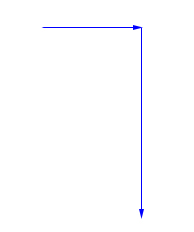
برای نشان جهت بردار جابجایی باید نقطه شروع حرکت (ابتدای بردار ۶ کیلومتری) را به انتهای مسیر (انتهای بردار ۱۳ کیلومتری) وصل کنیم. 

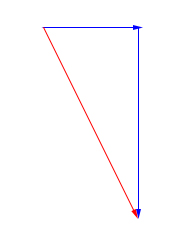
تصویر فوق، جمع دو بردار با استفاده از قانون مثلث را نشان می‌دهد. برای به‌دست آوردن اندازه بردار جابجایی از رابطه فیثاغورت استفاده می‌کنیم. چرا؟ زیرا بردارهای ۶ و ۱۳ کیلومتر بر یکدیگر عمود و دو ضلع مثلث قائم‌الزاویه‌ای را تشکیل می‌دهند که بردار جابجایی وتر آن است. در نتیجه اندازه بردار جابجایی برابر است با:

$$Displacement = sqrt { ( 13 ^ 2 ) + ( 6 ^ 2 ) } = 14.3 km$$

پرسش ۱: مسافت طی شده توسط فرد چند کیلومتر است؟

پاسخ: مسافت کمیتی اسکالر یا نرده‌ای و تنها دارای اندازه است. برای محاسبه مسافت به کل مسیر طی شده توسط فرد توجه می‌کنیم. از این‌رو، مقدار آن برابر ۱۹ کیلومتر است. 

پرسش ۲: مقدار زاویه $$theta$$ نشان داده شده در تصویر زیر چه مقدار است؟ 

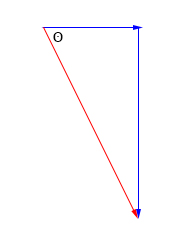
پاسخ: برای محاسبه $$theta$$ از رابطه زیر استفاده می‌کنیم:

$$tan theta = frac { 13 } { 6 } = 2.16 \ theta = 65.22 degree$$

مثال ۵

سارا پس از ۸ ساعت کار مداوم از محل کار خود خارج می‌شود. او برای رسیدن به خانه ابتدا ۲۶ کیلومتر به سمت شمال، سپس، با زاویه ۳۰ درجه نسبت به خط افق، ۶۲ کیلومتر به سمت شرق رانندگی می‌کند. جابجایی کل او چه مقدار است؟ 

مشاهده جواب

مسیر حرکت سارا در تصویر زیر نشان داده شده است. او ابتدا به سمت شمال حرکت می‌کند، سپس با تغییر مسیر خود، با زاویه ۳۰ درجه نسبت به خط افق، به سمت شرق به مسیر خود ادامه می‌دهد. 

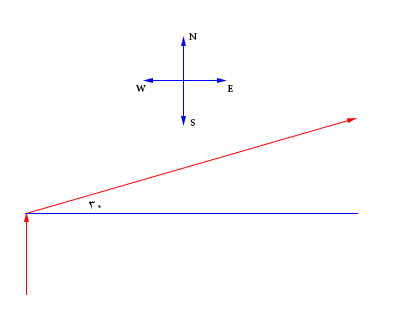
برای محاسبه جابجایی باید دو بردار نشان داده شده در تصویر فوق را با یکدیگر جمع کنیم. برای به‌دست آوردن جمع این دو بردار، ابتدا آن‌ها را به صورت نشان داده شده در تصویر زیر در دستگاه مختصات دکارتی رسم می‌کنیم. 

بردار با اندازه ۶۲ کیلومتر، با جهت مثبت محور $$x$$ زاویه ۶۰ درجه ساخته است. تصویر آن روی محور $$x$$ برابر $$62 times cos 30$$ و تصویر آن روی محور y برابر $$62 times sin 30 $$ خواهد بود. اندازه این بردار در راستای محور $$x$$ برابر ۵۳٫۷ کیلومتر و در راستای محور y برابر ۳۱ کیلومتر است. 

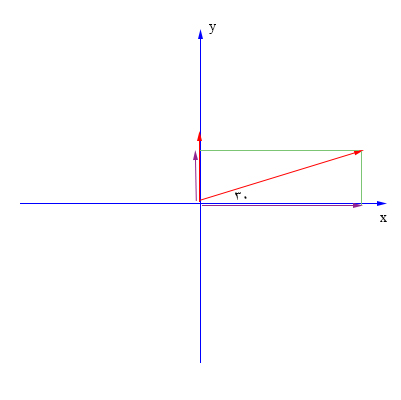
اکنون به راحتی می‌توانیم دو بردار ۶۲ و ۲۶ کیلومتری را با یکدیگر جمع کنیم. مجموع این دو بردار در راستای محور $$x$$ برابر است با: 

$$x: enspace 26 km + 31 km = 57 km $$

همچنین، مجموع دو بردار در راستای محور $$y$$ برابر است با: 

$$y: enspace 53.7 km $$

جمع دو بردار را با استفاده از قضیه فیثاغورث و قانون جمع مثلث به‌دست می‌آوریم. بردارهای ۵۳٫۷ و ۵۷ کیلومتر بر یکدیگر عمود و دو ضلع مثلث قائم‌الزاویه‌ای را تشکیل می‌دهند که بردار جابجایی وتر آن است. در نتیجه اندازه بردار جابجایی برابر است با:

$$Displacement = sqrt { ( 57) ^ 2  +(53.7) ^ 2 ) } = 78.3 km$$

مثال ۶

خواهر سیما یکی از وسایل مهم او را برداشته است و برای یافتن آن، سیما را به این صورت راهنمایی کرده است:

1. ۷۵ قدم با زاویه ۲۴۰ درجه حرکت کن.
2. سپس، ۱۲۵ قدم با زاویه ۱۳۵ درجه حرکت کن.
3. در پایان، ۱۰۰ قدم با زاویه ۱۶۰ درجه حرکت کن. 
4. این زاویه‌ها با توجه به جهت مثبت محور افقی اندازه گرفته شده‌اند.
5. تو به مقصد رسیدی.

جابجایی کل سیما چه مقدار است؟ 

مشاهده جواب

برای حل این مثال، باید بردارهای هر مسیر و زاویه مربوط به آن‌ها را با دقت رسم کنیم. با توجه به صورت سوال، زاویه‌ها با توجه به جهت مثبت محور افقی اندازه گرفته شده‌اند. ابتدا بردارها را روی کاغذ شطرنجی به صورت جداگانه رسم، سپس آن‌ها را در دستگاه مختصات دکارتی دوبعدی نشان می‌دهیم. 

در ادامه، این بردارها را به صورت نشان داده شده در تصویر زیر روی دستگاه مختصات دکارتی رسم می‌کنیم. 

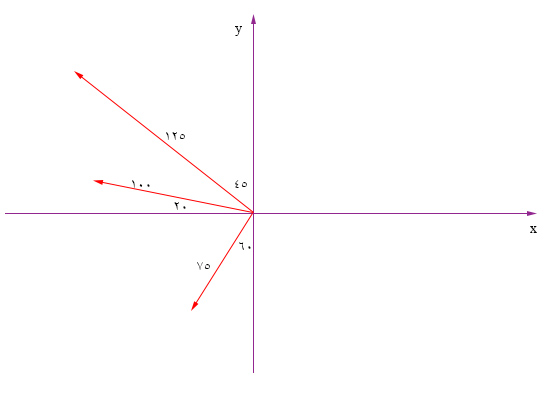
ابتدا بردار با اندازه ۷۵ را تجزیه می‌کنیم. زاویه این بردار با جهت منفی محور $$y$$ برابر ۶۰ درجه است:

$$75:begin{cases}x: -75cos 60 = – 37.5 \ y: -75 sin 60 =- 64.95 end{cases} $$

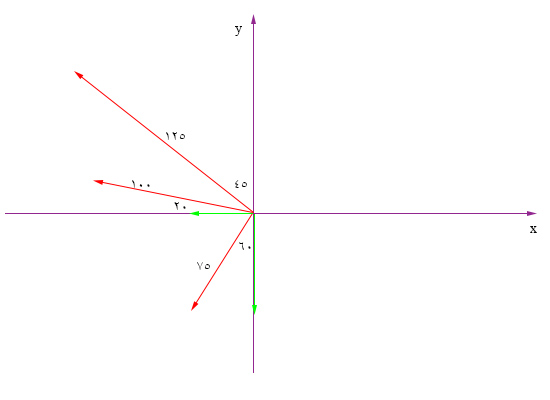
در ادامه، بردار با اندازه ۱۲۵ را تجزیه می‌کنیم. زاویه این بردار با جهت مثبت محور $$y$$ برابر ۴۵ درجه است:

$$75:begin{cases}x: – 125sin 45 = – 88.4 \ y: 125 cos 45 = 88.4 end{cases} $$

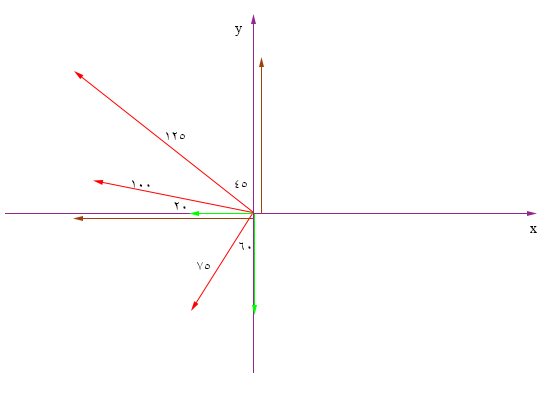
در پایان، بردار با اندازه ۱۰۰ را تجزیه می‌کنیم. زاویه این بردار با جهت منفی محور $$x$$ برابر ۲۰ درجه است:

$$75:begin{cases}x: – 100 cos 20 = – 93.97 \ y: 100 sin 20 = 34.20 end{cases} $$

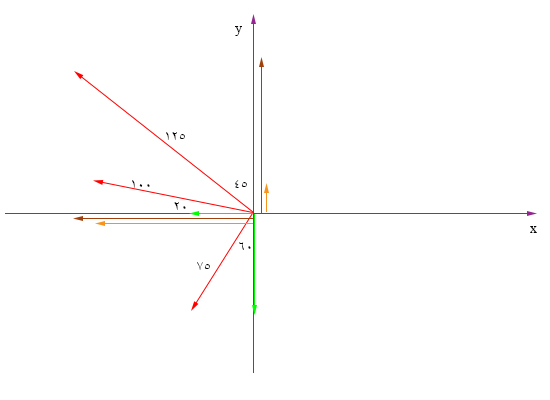
اکنون به راحتی می‌توانیم بردارها را در راستای محور $$x$$ و محور‌ $$y$$ با یکدیگر جمع کنیم. مجموع بردارها در راستای محور $$x$$ برابر ۲۱۹٫۸- و در راستای محور $$y$$ برابر ۵۷٫۶۵ است. این دو بردار بر یکدیگر عمود هستند. در نتیجه، بردار کل را می‌توانیم با استفاده از قضیه فیثاغورث به‌دست آوریم:

$$Displacement = sqrt { ( 57.65) ^ 2  + ( -219.8)^ 2} = 227 paces$$

چگونه بردارها را با یکدیگر ضرب کنیم؟

تا اینجا می‌دانیم کمیت برداری چیست و چگونه کمیت‌های برداری را با یکدیگر جمع کنیم. در این بخش، در مورد ضرب بردارها توضیح می‌دهیم. در حالت کلی، سه نوع ضرب برداری داریم:

1. ضرب عدد یا کمیت اسکالر در بردار
2. ضرب داخلی یا نقطه‌‌ای کمیت‌های برداری
3. ضرب خارجی کمیت‌های برداری

ضرب عدد در بردار

بردار ممکن است، یک، دو یا سه مولفه داشته باشد. فرض کنید برداری مانند $$overrightarrow{a}$$ داریم که سه مولفه به صورت زیر دارد:

$$overrightarrow{a}= (a_1, a_2 , a_ 3) $$

اندازه این بردار برابر $$|overrightarrow{ a }|$$ است. عدد n را در این بردار ضرب می‌کنیم. اندازه آن چگونه تغییر می‌کند؟ هنگامی‌که عدد یا کمیتی اسکالر را در برداری ضرب می‌کنیم، آن عدد در تک‌ تکِ مولفه‌های آن بردار به صورت زیر ضرب می‌شود:

$$n overrightarrow{ a }= n (a_1, a_2 , a_ 3 ) = ( n a_1
, n a_ 2 , n a _ 3 ) $$

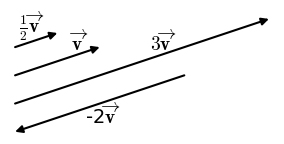
در نتیجه، اندازه بردار $$|overrightarrow{ a }|$$ پس از ضرب آن در عدد n برابر $$|n overrightarrow{ a }|$$ خواهد بود. به هنگام ضرب عدد در بردار باید به دو نکته توجه داشته باشیم:

• اگر n عددی مثبت باشد، اندازه بردار n برابر و جهت آن بدون تغییر باقی می‌ماد.
• اگر n عددی منفی باشد، اندازه بردار n برابر و جهت آن نیز مخالف جهت بردار اولیه می‌شود.

مهم‌ترین ویژگی‌های ضرب عدد در بردار عبارت هستند از:

• حاصل‌ضرب عدد در بردار شرکت‌پذیر است:

$$c(d overrightarrow{a}) = (cd) overrightarrow{ a }$$

• حاصل‌ضرب عدد در بردار جابجاپذیر است:

$$c overrightarrow{a} = overrightarrow{ a }c$$

• حاصل‌ضرب عدد در بردار توزیع‌پذیر است:

$$( c + d ) overrightarrow{a} = c overrightarrow{ a } +
d overrightarrow{ a } \ c ( overrightarrow{ a } +
overrightarrow{ b } ) = c overrightarrow{ a } + c
overrightarrow{ b }$$

• حاصل‌ضرب صفر در هر برداری برابر صفر است.

ضرب نقطه ای کمیت های برداری

در بخش‌های قبل به پرسش کمیت برداری چیست به زبان ساده پاسخ دادیم و با جمع، تفریق، تجزیه و ضرب عدد در کمیت‌های برداری آشنا شدیم. در این بخش با ضرب دو بردار با یکدیگر آشنا می‌شویم. به این نکته توجه داشته باشید که ضرب دو بردار در یکدیگر مانند ضرب اعداد یا کمیت‌های اسکالر در یکدیگر نیست. بردارها به دو روش می‌توانند در یکدیگر ضرب شوند:

1. ضرب نقطه‌ای یا داخلی بردارها
2. ضرب خارجی بردارها

در این بخش در مورد ضرب نقطه‌ای دو بردار با یکدیگر صحبت می‌کنیم. فرض کنید دو بردار $$overrightarrow{ a }$$ و $$overrightarrow{ b }$$ به صورت زیر داریم:

$${ {overrightarrow{ a } = (a_ 1 , a_ 2 , a _ 3) }} \{overrightarrow{ b } = ( b_ 1 , b_2b_ 3 ) } $$

ضرب نقطه‌ای یا داخلی دو بردار به صورت زیر نوشته می‌شود:

$$ {overrightarrow { a } . overrightarrow{ b }}$$

مهم‌ترین نکته‌های ضرب نقطه‌ای دو بردار عبارت هستند از:

• حاصل ضرب نقطه‌ای دو بردار، عدد یا کمیتی اسکالر است.
• به هنگام محاسبه ضرب نقطه‌ای دو بردار، مولفه‌های متناظر را به صورت زیر با یکدیگر ضرب و سپس، حاصل ضرب آن‌ها را با هم جمع می‌کنیم.

$$overrightarrow{ a } . overrightarrow{ b } = (a_1
b_1) + (a_2 b _ 2 ) + ( a_ 3 b_ 3 ) $$

بنابراین، ضربه نقطه‌ای، دو کمیت برداری را به عنوان ورودی از ما می‌گیرید و عددی را به عنوان خروجی به ما می‌دهد. به عنوان مثال، اگر بردار $$overrightarrow{ a } $$ برابر $$overrightarrow{ a } = ( 2 , 4 )  $$ و بردار $$overrightarrow{ b } $$ برابر $$overrightarrow{ b } = ( 1 , -3 )  $$ باشند، حاصل $$overrightarrow{ a } . overrightarrow{ b } $$ برابر است با:

$$overrightarrow{ a } . overrightarrow{ b } = [(2 ) (
1)] + [(4) (-3 )] = 2 – 12 = -10 $$

ضرب نقطه‌ای دو بردار، جابجا پذیر است. به بیان ساده‌تر، حاصل $$overrightarrow{ a } . overrightarrow{ b } $$ با $$overrightarrow{ b } . overrightarrow{ a } $$ برابر است. همچنین، ضرب نقطه‌ای بردارها ویژگی مهم دیگر به نام توزیع‌پذیری دارد:

$$overrightarrow{ a }.(overrightarrow{ b } +
overrightarrow{ c }) = ( overrightarrow{ a } .
overrightarrow{ b }) + ( overrightarrow{ a } .
overrightarrow{ c })$$

فرض کنید دو بردار $$overrightarrow{ a }$$ و $$overrightarrow{ b }$$ داریم. اگر بردار $$overrightarrow{ a }$$ در کمیتی اسکالر به نام c ضرب شود، ضرب نقطه‌ای بردارهای $$overrightarrow{  c a }$$ و $$overrightarrow{ b }$$ را می‌توانیم به صورت زیر بنویسیم:

$$( c overrightarrow{ a }) . overrightarrow { b }$$

حاصل‌ضرب $$( c overrightarrow{ a }) . overrightarrow { b }$$ را می‌توانیم به دو صورت $$ c( overrightarrow{ a } . overrightarrow { b }) $$ و $$ overrightarrow{ a } . (coverrightarrow { b })$$ نیز بنویسیم. از این‌رو، فرقی ندارد کدام‌یک از دو بردار در ضرب نقطه‌ای در کمیتی اسکالر ضرب شود، پاسخ ضرب یکسان خواهد بود. آیا می‌توانیم یک بردار را در خودش به صورت نقطه‌ای ضرب کنیم؟ بله، اگر بردار $$overrightarrow{ a }$$ را به صورت نقطه‌ای در خودش ضرب کنیم، حاصل به‌دست آمده برابر طول این بردار است:

$$ overrightarrow{ a } . overrightarrow{ a }= |a|^ 2$$

اگر بردار صفر را در بردار دلخواهی ضرب کنیم، حاصل برابر صفر خواهد بود. فرض کنید زاویه بین دو بردار $$overrightarrow{ a }$$ و $$overrightarrow{ b }$$ برابر $$theta $$ است.

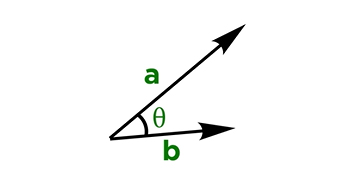
در این حالت، علاوه بر ضرب مولفه‌های متناظر با یکدیگر و جمع آن‌ها، ضرب نقطه‌ای را می‌توانیم به صورت زیر نیز به‌دست آوریم:

$$overrightarrow { a } . overrightarrow { b } = | overrightarrow{a }| | overrightarrow{ b } | cos theta $$

بنابراین، برای محاسبه زاویه بین دو بردار، به راحتی می‌توانیم از رابطه زیر استفاده کنیم:

$$cos theta = frac { overrightarrow { a } . overrightarrow { b } } {| overrightarrow{a }| | overrightarrow{ b } | }$$

مثال محاسبه زاویه بین دو بردار

زاویه بین دو بردار $$overrightarrow { a } = ( 2 , 2 , -1) $$ و $$overrightarrow { b } = ( 5 , -3 , 2 ) $$ را به‌دست آور.

پاسخ

زاویه بین دو بردار را می‌توانیم با استفاده از رابطه زیر به‌دست آوریم:

$$cos theta = frac { overrightarrow { a } . overrightarrow { b } } {| overrightarrow{a }| | overrightarrow{ b } | }$$

ابتدا اندازه هر بردار را به‌دست می‌آوریم:

$$ overrightarrow{ a } . overrightarrow{ a }= |a|^ 2\ |a | ^ 2 = ( 2 , 2 , -1) . (2 , 2 , -1 ) = 4+4+1 = 9Rightarrow | a | = 3\ | b | ^ 2 =( 5 , -3 , 2 ) . ( 5 , -3 , 2 ) = 25 + 9 + 4 = 38 rightarrow | b | =6.2 $$

همچنین، ضرب نقطه‌ای بین دو بردار را نیز به صورت زیر محاسبه می‌کنیم:

$$ overrightarrow{ a } . overrightarrow{ b }= [ ( 2 ) ( 5 ) ] + [ ( 2 ) ( -3 ) ] + [ ( – 1 ) ( 2 ) ] = 10 -6 -2 = 2 $$

با قرار دادن مقدارهای به‌دست آمده در رابطه $$cos theta = frac { overrightarrow { a } . overrightarrow { b } } {| overrightarrow{a }| | overrightarrow{ b } | }$$، زاویه بین دو بردار را به‌دست می‌آوریم:

$$cos theta = frac { overrightarrow { a } . overrightarrow { b } } {| overrightarrow{a }| | overrightarrow{ b } | } = frac { 2 } { 6.2 times 3 } = frac { 1 } { 3.1 times 3 } \ theta = 85 degree $$

پرسش: چه هنگامی ضرب نقطه‌ای بین دو بردار برابر صفر است؟

پاسخ: اگر زاویه بین دو بردار برابر ۹۰ درجه باشد، ضرب نقطه‌ای بین آن‌ها برابر برابر صفر است.

با توجه به پرسش مطرح شده در بالا، به راحتی می‌توانیم حاصلِ ضرب نقطه‌ای بین بردارهای یکه را به‌دست آوریم:

$$widehat{ i }. widehat{ j }= | widehat{ i } | | widehat{ j } | cos 90^ o = (1 ) ( 1) ( 0 ) = 0 \ widehat{ i }. widehat{ k }= | widehat{ i } | | widehat{ k } | cos 90^ o = (1 ) (1 ) ( 0 ) = 0 \ widehat{ k }. widehat{ j }= | widehat{ k } | | widehat{ j } | cos 90^ o = (1 ) ( 1 ) ( 0 ) = 0$$

نکته: بردارهای یکه، بردارهای واحد و اندازه آن‌ها برابر یک است.

در این بخش با ضرب نقطه‌ای کمیت‌های برداری آشنا شدیم. در ادامه و به منظور آشنایی بیشتر با این مبحث، مثال‌هایی را با یکدیگر حل می‌کنیم.

مثال ۱

دو بردار $$overrightarrow { a } $$ و $$overrightarrow {  b } $$ به صورت زیر داده شده‌اند: 

$$overrightarrow{ a } = (0, 4 , -2 ) \ overrightarrow{ b } = 2 widehat{ i } – widehat{ j } + 7 widehat{ k }$$

حاصل $$overrightarrow { a } . overrightarrow { b } $$ برابر است با: 

مشاهده جواب

ضربه نقطه‌ای، دو کمیت برداری را به عنوان ورودی از ما می‌گیرید و عددی را به عنوان خروجی به ما می‌دهد. به هنگام محاسبه ضرب نقطه‌ای دو بردار، مولفه‌های متناظر را به صورت زیر با یکدیگر ضرب و سپس، حاصل ضرب آن‌ها را با هم جمع می‌کنیم.

$$overrightarrow{ a } . overrightarrow{ b } = (a_1
b_1) + (a_2 b _ 2 ) + ( a_ 3 b_ 3 ) $$

اگر کمیت‌های برداری برحسب مولفه‌های یکه $$widehat{ i }$$ و $$widehat{ j }$$ و $$widehat{ k }$$ نوشته شده باشند، به هنگام محاسبه ضرب داخلی بین آن‌ها، باید مولفه‌های یکه متناظر را با یکدیگر ضرب کنیم:

$$widehat{ i }. widehat{ j }= | widehat{ i } | | widehat{ j } | cos 90^ o = (1 ) ( 1) ( 0 ) = 0 \ widehat{ i }. widehat{ k }= | widehat{ i } | | widehat{ k } | cos 90^ o = (1 ) (1 ) ( 0 ) = 0 \ widehat{ k }. widehat{ j }= | widehat{ k } | | widehat{ j } | cos 90^ o = (1 ) ( 1 ) ( 0 ) = 0$$

بردارهای $$overrightarrow { a } $$ و $$overrightarrow {  b } $$ به صورت زیر داده شده‌اند:

$$overrightarrow{ a } = (0, 4 , -2 ) \ overrightarrow{ b } = 2 widehat{ i } – widehat{ j } + 7 widehat{ k }$$

برای محاسبه $$overrightarrow { a } . overrightarrow { b } $$ می‌توانیم بردار $$overrightarrow { a } $$ را نیز مشابه بردار $$overrightarrow {  b } $$ برحسب مولفه‌های یکه بنویسیم:

$$ overrightarrow{ a } = 0 widehat{ i } + 4 widehat{ j } -2 widehat{ k } = 4 widehat{ j } -2 widehat{ k }$$

در نتیجه، حاصل $$overrightarrow { a } . overrightarrow { b } $$ برابر است با: 

$$overrightarrow { a } . overrightarrow { b } = (4 widehat{ j } -2 widehat{ k }) . ( 2 widehat{ i } – widehat{ j } + 7 widehat{ k }) \= 8 (widehat { j }. widehat { i } ) – 4 (widehat { j } . widehat { j } )+ 28 (widehat { j } . widehat { k } ) -4 (widehat { k } . widehat { i }) + 2 (widehat { k } . widehat { j } )-14 (widehat { k } . widehat { k } ) \ = -4 -14 = – 18 $$

مثال ۲ 

اگر اندازه بردار $$overrightarrow { a }$$ برابر ۵، اندازه بردار $$overrightarrow { b }$$ برابر $$frac { 3 } { 7 } $$ و زاویه بین آن‌ها برابر $$frac { pi} { 12 } $$ باشد، حاصل $$overrightarrow { a } . overrightarrow { b } $$ کدام است؟ 

مشاهده جواب

اگر اندازه و زاویه بین دو بردار $$overrightarrow { a }$$ و $$overrightarrow { b }$$ را داشته باشیم، ضرب نقطه‌ای بین آن‌ها را می‌توانیم به صورت زیر به‌دست آوریم:

$$overrightarrow { a } . overrightarrow { b } = | overrightarrow{a }| | overrightarrow{ b } | cos theta $$

با قرار دادن مقدارهای داده شده در رابطه فوق، حاصل $$overrightarrow { a } . overrightarrow { b } $$ را به‌دست می‌‌آوریم:

$$overrightarrow { a } . overrightarrow { b } \ = ( 5 ) (frac { 3 } { 7 } ) cos (frac { pi } { 12 } ) = frac { 15 } { 7 } times 0.97 = 2.1 $$

مثال ۳

دو بردار $$overrightarrow { u } $$ و $$overrightarrow { w } $$ به صورت  زیر داده شده‌اند:

$$overrightarrow{ u } = 7 widehat{ i } – widehat{ j } + widehat{ k } \ overrightarrow{ w } = -2 widehat{ i } +5 widehat{ j } – 6 widehat{ k }$$

تصویر بردار $$overrightarrow { u } $$ در امتداد بردار $$overrightarrow { w } $$ کدام است؟ 

$$frac { 10 } { 13 } widehat { i } – frac { 25 } { 13 } widehat { j } + frac { 3 0 } { 13 } widehat { k }$$

$$frac { 10 } { 13 } widehat { i } + frac { 25 } { 13 } widehat { j } – frac { 3 0 } { 13 } widehat { k }$$

$$frac { 10 } { 13 } widehat { i } – frac { 25 } { 13 } widehat { j } – frac { 3 0 } { 13 } widehat { k }$$

$$frac { 30 } { 13 } widehat { i } – frac { 25 } { 13 } widehat { j } + frac { 1 0 } { 13 } widehat { k }$$

مشاهده جواب

تصویر بردار $$overrightarrow { u } $$ در امتداد بردار $$overrightarrow { w } $$ با استفاده از رابطه زیر به‌دست می‌آید:

$$proj _ { overrightarrow{ w } } overrightarrow{ u } = frac { overrightarrow{ u } . overrightarrow{ w }} { | overrightarrow{ w } | ^ 2 } (overrightarrow{ w } ) $$

ابتدا ضرب داخلی $$overrightarrow{ u } . overrightarrow{ w } $$ را به‌دست می‌آوریم:

$$overrightarrow{ u } . overrightarrow{ w } = ( 7 widehat{ i } – widehat{ j } + widehat{ k } ) .( -2 widehat{ i } +5 widehat{ j } – 6 widehat{ k }) = -14 -5 -6 = -25 $$

همچنین، اندازه بردار $$overrightarrow { w } $$ برابر است با: 

$$ overrightarrow{ w } . overrightarrow{ w }= |w|^ 2 \ | w | ^ 2 = ( -2 widehat{ i } +5 widehat{ j } – 6 widehat{ k }) .( -2 widehat{ i } +5 widehat{ j } – 6 widehat{ k }) = 4+25+36 = 65$$

در نتیجه، تصویر بردار $$overrightarrow { u } $$ در امتداد بردار $$overrightarrow { w } $$ برابر است با: 

$$proj _ { overrightarrow{ w } } overrightarrow{ u } = frac { overrightarrow{ u } . overrightarrow{ w }} { | overrightarrow{ w } | ^ 2 } (overrightarrow{ w } ) = frac { -25 } { 65 } ( -2 widehat{ i } +5 widehat{ j } – 6 widehat{ k }) \ proj _ { overrightarrow{ w } } = frac { -5 } { 13 } ( -2 widehat{ i } +5 widehat{ j } – 6 widehat{ k }) = frac { 10 } { 13 } widehat { i } – frac { 25 } { 13 } widehat { j } + frac { 3 0 } { 13 } widehat { k } $$

ضرب خارجی کمیت های برداری

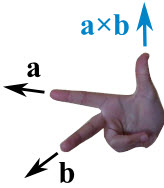
در بخش‌های قبل با ضرب نقطه‌ای دو بردار آشنا شدیم. در این بخش با ضرب خارجی دو بردار با یکدیگر آشنا می‌شویم. به این نکته توجه داشته باشید که ضرب دو بردار در یکدیگر مانند ضرب اعداد یا کمیت‌های اسکالر در یکدیگر نیست. بردارها به دو روش نقطه‌ای و خارجی در یکدیگر ضرب می‌شوند. حاصل ضرب نقطه‌ای دو بردار، کمیتی اسکالر یا عدد و حاصل ضرب برداری دو بردار با یکدیگر، کمیتی برداری و عمود بر دو بردار است. ضرب خارجی بین دو بردار با علامت $$times$$ نشان داده می‌شود.

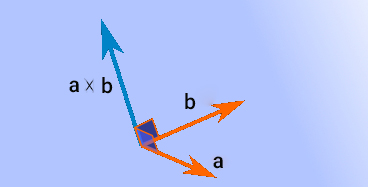
اندازه یا طول بردارِ حاصل از ضرب خارجی دو بردار $$overrightarrow{ a } $$ و $$overrightarrow{ a } $$ برابر مساحت متوازی‌الاضلاع ساخته شده توسط این دو بردار است (تصویر زیر).

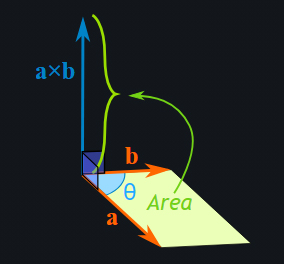
جهت و اندازه بردار $$overrightarrow{ a } times overrightarrow{ b }$$ به عامل‌های زیر وابسته است:

• زاویه بین دو بردار
• اندازه دو بردار

با تغییر زاویه بین دو بردار، اندازه و جهت بردار $$overrightarrow{ a } times overrightarrow{ b }$$ تغییر می‌کند. اگر بردار $$overrightarrow{  a  }$$ ثابت و جهت بردار $$overrightarrow{ b } $$ تغییر کند، اندازه و جهت بردار $$overrightarrow{ a } times overrightarrow{ b }$$ به صورت نشان داده در تصویر زیر، تغییر خواهد کرد.

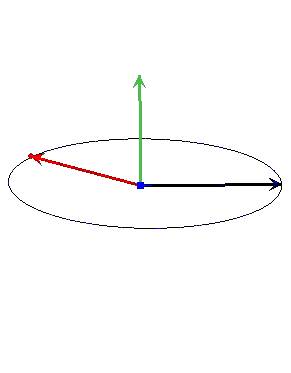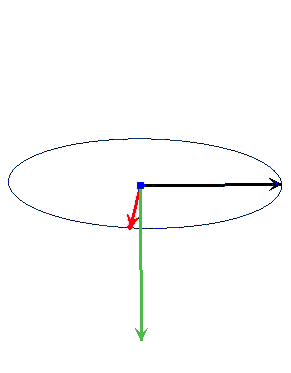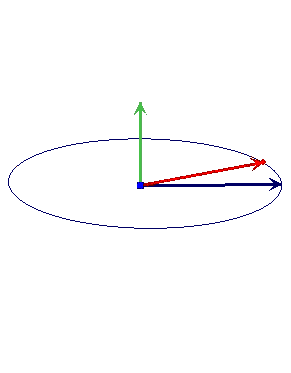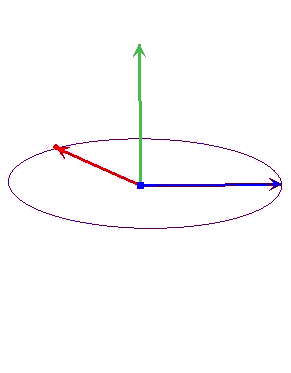
اگر زاویه بین دو بردار $$overrightarrow{  a  }$$ و $$overrightarrow{ b } $$ برابر صفر یا ۱۸۰ (بردارهای موازی) باشد، حاصل $$overrightarrow{ a } times overrightarrow{ b }$$ برابر صفر و اگر دو بردار بر یکدیگر عمود باشند، حاصل $$overrightarrow{ a } times overrightarrow{ b }$$ بیشینه است. ضرب خارجی دو بردار را به دو روش می‌توان محاسبه کرد.

روش اول محاسبه ضرب خارجی کمیت های برداری

$$overrightarrow{  a  }$$ و $$overrightarrow{ b } $$ را می‌توان با استفاده از رابطه زیر به‌دست آورد:

$$overrightarrow{ a } times overrightarrow{ b } = | overrightarrow{ a } | | overrightarrow{ b } | sin theta widehat{ n }$$

در رابطه فوق:

• $$ | overrightarrow{ a } | $$ اندازه بردار $$overrightarrow{ a } $$ است.
• $$ | overrightarrow{  b } | $$ اندازه بردار $$overrightarrow{b  } $$ است.
• $$theta $$ زاویه بین دو بردار $$overrightarrow{ a } $$ و $$overrightarrow{ a } $$ است.
• $$widehat{ n } $$ بردار واحدی عمود بر بردارهای $$overrightarrow{ a } $$ و $$overrightarrow{ a } $$ است.

روش دوم محاسبه ضرب خارجی کمیت های برداری

ضرب خارجی دو بردار را با استفاده از ماتریس نیز می‌توانیم به‌دست آوریم. فرض کنید دو بردار $$overrightarrow{ a } $$ و $$overrightarrow{ a } $$ به صورت زیر داریم:

$$overrightarrow{ a } = ( 1 , 3 , 4 ) \ overrightarrow { b } = ( 2 , 7 , -5 ) $$

این دو بردار را می‌توانیم برحسب بردارهای یکه به صورت زیر بنویسیم:

$$overrightarrow{ a } = widehat{ i } + 3 widehat{ j } + 4 widehat{ k } \ overrightarrow{ b } = 2 widehat{ i } + 7 widehat{ j } -5 widehat{ k }$$

برای محاسبه ضرب خارجی این دو بردار، تنها کافی است دترمینان ماتریس زیر را به‌دست آوریم:

$$overrightarrow{ a } times overrightarrow { b } = ( widehat{ i } + 3 widehat{ j } + 4 widehat{ k } ) times ( 2 widehat{ i } + 7 widehat{ j } -5 widehat{ k } ) = det begin{bmatrix} i & j & k \ 1 & 3 & 4 \ 2 & 7 & – 5 end{bmatrix}$$

با توجه به رابطه فوق، دترمینان ضرب خارجی دو بردار به صورت زیر نوشته می‌شود:

• سطر اول دترمینان از بردارهای یکه $$widehat { i } $$ و $$widehat { j } $$ و $$widehat { k } $$ تشکیل شده است.
• سطر دوم دترمینان از مولفه‌های نخستین بردار در ضرب خارجی تشکیل شده است.
• سطر سوم دترمینان از مولفه‌های دومین بردار در ضرب خارجی تشکیل شده است.

برای آشنا با چگونگی محاسب دترمینان می‌توانید به مطلب «دترمینان یک ماتریس و محاسبه آن — به زبان ساده» از مجله فرادرس مراجعه کنید. دترمینان ماتریس فوق برابر است با:

$$ det begin{bmatrix} i & j & k \ 1 & 3 & 4 \ 2 & 7 & – 5 end{bmatrix} = det begin{bmatrix} 3 & 4 \ 7 & -5 end{bmatrix} widehat { i } – det begin{bmatrix} 1 & 4 \ 2 & -5 end{bmatrix} widehat {  j} + det begin{bmatrix} 1 & 3 \ 2 & 7 end{bmatrix} widehat { k } \ = (-15 – 28 ) widehat { i } – ( -5 – 8 ) widehat { j } +( 7 – 6 ) widehat { k } \ = -43 widehat { i } +13 widehat { j } + widehat { k } $$

بردار $$-43 widehat { i } +13 widehat { j } + widehat { k } $$ بر بردارهای $$overrightarrow{ a } $$ و $$overrightarrow{ a } $$ عمود است. برای اطمینان از این موضوع می‌توانیم حاصل $$overrightarrow{ a }. ( overrightarrow{a } times overrightarrow{ b } )$$ و $$overrightarrow{ b }. ( overrightarrow{a } times overrightarrow{ b } )$$ را به‌دست آوریم.

$$overrightarrow{ a }. ( overrightarrow{a } times overrightarrow{ b } ) = ( widehat{ i } + 3 widehat{ j } + 4 widehat{ k }) . (- 43 widehat { i } +13 widehat { j } + widehat { k }) \ = -43+39+4 = 0 \ overrightarrow{ b }. ( overrightarrow{a } times overrightarrow{ b } ) = ( 2 widehat{ i } + 7 widehat{ j } -5 widehat{ k }) . (-43 widehat { i } +13 widehat { j } + widehat { k }) \ = -86+91 -5 = 0$$

جهت بردار $$overrightarrow{ a } times overrightarrow{ b }$$ را می‌توانیم با استفاده از قانون درست راست، به صورت نشان داده شده در تصویر زیر، به‌دست آوریم.

ضرب خارجی هر بردار در خودش همواره برابر صفر است. فرض کنید بردار $$overrightarrow { a }$$ با مولفه‌های a و b و c داریم. حاصل $$overrightarrow { a } times overrightarrow { a } $$ برابر است با:

$$overrightarrow{ a } times overrightarrow { a } = ( a widehat{ i } + b widehat{ j } + c widehat{ k } ) times ( a widehat{ i } + b widehat{ j } + c widehat{ k } ) = det begin{bmatrix} i & j & k \ a & b & c \ a & b & c end{bmatrix} \ det begin{bmatrix} i & j & k \ a & b & c \ a & b & c end{bmatrix} = det begin{bmatrix} b & c\ b & c end{bmatrix} widehat { i } – det begin{bmatrix} a & c \ a & -5 end{bmatrix} widehat { j } + det begin{bmatrix} a & b \ a & b end{bmatrix} widehat { k } \ = (bc – bc ) widehat { i } – ( ac – ac ) widehat { j } +( ab – ab ) widehat { k } \ = 0 widehat { i } + 0 widehat { j } + 0 widehat { k } $$

مهم‌ترین ویژگی‌های ضرب خارجی کمیت‌های برداری عبارت هستند از:

• ضرب خارجی دو بردار جابجاپذیر نیست.

$$overrightarrow { a } times overrightarrow { b } neq overrightarrow { b } times overrightarrow { a } $$

• ضرب خارجی $$overrightarrow { a } times overrightarrow{ b } $$ برابر $$- overrightarrow { b } times overrightarrow{ a } $$ است.
• ضرب خارجی بردارها شرکت‌پذیر نیست.

$$( overrightarrow { a } times overrightarrow{ b }) times overrightarrow{ c } neq overrightarrow { a } times ( overrightarrow{ b } times overrightarrow{ c }) $$

• ضرب خارجی بردارها توزیع‌پذیر است.

$$ overrightarrow { a } times ( overrightarrow{ b } + overrightarrow{ c } ) = (overrightarrow { a } times overrightarrow{ b } ) + (overrightarrow { a } times overrightarrow{ c }) $$

تا اینجا با دو روش محاسبه ضرب برداری آشنا شدیم. در ادامه، برای درک بهتر این مبحث چند مثال را با یکدیگر حل می‌کنیم.

مثال ۱

اندازه بردار $$overrightarrow  { a } $$ برابر ۳، اندازه بردار $$overrightarrow { b } $$ برابر ۴ و زاویه بین این دو بردار برابر ۳۰ درجه است. حاصل $$overrightarrow { a } times overrightarrow { b } $$ کدام است؟ ($$widehat { n } $$ بردار واحد و بر بردارهای $$overrightarrow  { a } $$ و $$overrightarrow { b } $$ عمود است)

مشاهده جواب

ضرب خارجی دو بردار $$overrightarrow{  a  }$$ و $$overrightarrow{ b } $$ را می‌توان با استفاده از رابطه زیر به‌دست آورد:

$$overrightarrow{ a } times overrightarrow{ b } = | overrightarrow{ a } | | overrightarrow{ b } | sin theta widehat{ n }$$

مقدارهای داده شده را در رابطه بالا قرار می‌دهیم: 

$$overrightarrow{ a } times overrightarrow{ b } = | overrightarrow{ a } | | overrightarrow{ b } | sin theta widehat{ n } \ = (3 ) ( 4 ) sin (30) widehat { n } = (12) (frac { 1 } { 2 } ) widehat { n } = 6 widehat { n } $$

مثال ۲

اندازه بردار $$overrightarrow  { a } $$ برابر $$3 sqrt { 2 } $$، اندازه بردار $$overrightarrow { b } $$ برابر ۵ و زاویه بین این دو بردار برابر ۱۳۵ درجه است. حاصل $$overrightarrow { a } times overrightarrow { b } $$ کدام است؟ ($$widehat { n } $$ بردار واحد و بر بردارهای $$overrightarrow  { a } $$ و $$overrightarrow { b } $$ عمود است)

$$- 15 sqrt { 2 } widehat { 2 } $$

$$15 sqrt { 2 } widehat { n } $$

مشاهده جواب

ضرب خارجی دو بردار $$overrightarrow{  a  }$$ و $$overrightarrow{ b } $$ را می‌توان با استفاده از رابطه زیر به‌دست آورد:

$$overrightarrow{ a } times overrightarrow{ b } = | overrightarrow{ a } | | overrightarrow{ b } | sin theta widehat{ n }$$

مقدارهای داده شده را در رابطه بالا قرار می‌دهیم: 

$$overrightarrow{ a } times overrightarrow{ b } = | overrightarrow{ a } | | overrightarrow{ b } | sin theta widehat{ n } \ = (3 sqrt { 2 } ) ( 5 ) sin (135) widehat { n } = (15 sqrt { 2 } ) (frac { sqrt { 2 } } { 2 } ) widehat { n } = 15 widehat { n } $$

مثال ۳

حاصل ضرب خارجی دو بردار $$overrightarrow{ a } = (1, 2 , 3) $$ و $$overrightarrow{ b } = (4 , 5 , 6) $$ برابر است با:

مشاهده جواب

ضرب خارجی دو بردار را با استفاده از ماتریس نیز می‌توانیم به‌دست آوریم. فرض کنید دو بردار $$overrightarrow{ a } $$ و $$overrightarrow{ a } $$ به صورت زیر داریم:

$$overrightarrow{ a } = ( 1 , 2 , 3 ) \ overrightarrow { b } = ( 4 , 5 , 6 ) $$

این دو بردار را می‌توانیم برحسب بردارهای یکه به صورت زیر بنویسیم:

$$overrightarrow{ a } = widehat{ i } + 2 widehat{ j } + 3 widehat{ k } \ overrightarrow{ b } = 4 widehat{ i } + 5 widehat{ j } + 6 widehat{ k }$$

برای محاسبه ضرب خارجی این دو بردار، تنها کافی است دترمینان ماتریس زیر را به‌دست آوریم:

$$overrightarrow{ a } times overrightarrow { b } = ( widehat{ i } + 2 widehat{ j } +3 widehat{ k } ) times ( 4 widehat{ i } + 5 widehat{ j } + 6 widehat{ k } ) = det begin{bmatrix} i & j & k \ 1 & 2 & 3 \ 4 & 5 & 6 end{bmatrix}$$

دترمینان ماتریس فوق برابر است با:

$$ det begin{bmatrix} i & j & k \ 1 & 2 & 3 \ 4 & 5 & 6 end{bmatrix} = det begin{bmatrix} 2 & 3 \ 5 & 6 end{bmatrix} widehat { i } – det begin{bmatrix} 1 & 3 \ 4 & 6 end{bmatrix} widehat {  j } + det begin{bmatrix} 1 & 2 \ 4 & 5 end{bmatrix} widehat { k } \ = (12 – 15 ) widehat { i } – ( 6 – 12 ) widehat { j } + ( 5 – 8 ) widehat { k } \ = -3 widehat { i } + 6 widehat { j } – 3 widehat { k } =( -3, 6 , -3 ) $$

مثال ۴

اگر $$overrightarrow{ a } = ( -2 , 1 , 1 )$$ و $$overrightarrow{ b } = ( 2 , 1 , 1 )$$ و $$overrightarrow { c } = overrightarrow { a } times overrightarrow { b } $$ باشند، اندازه بردار $$overrightarrow { c } $$ چه مقدار است؟ 

مشاهده جواب

برای محاسبه اندازه $$overrightarrow { c } $$ ابتدا حاصل $$overrightarrow{a}times overrightarrow{b} $$ را به‌دست می‌آوریم. برای محاسبه ضرب خارجی این دو بردار، تنها کافی است دترمینان ماتریس زیر را محاسبه کنیم:

$$overrightarrow{ a } times overrightarrow { b } = (-2 widehat{ i } + widehat{ j } + widehat{ k } ) times ( 2 widehat{ i } + 2 widehat{ j } + 2 widehat{ k } ) = det begin{bmatrix} i & j & k \ -2 & 1 & 1 \ 2 & 1 & 1 end{bmatrix}$$

دترمینان ماتریس فوق برابر است با:

$$ det begin{bmatrix} i & j & k \ -2 & 1 & 1 \ 2 & 1 & 1 end{bmatrix} = det begin{bmatrix} 1 & 1 \ 1 & 1 end{bmatrix} widehat { i } – det begin{bmatrix} -2 & 1 \ 2 & 1 end{bmatrix} widehat {  j } + det begin{bmatrix} -2 & 1 \ 2 & 1 end{bmatrix} widehat { k } \ = ( 1 – 1 ) widehat { i } – ( -2 – 2 ) widehat { j } + ( -2 – 2 ) widehat { k } \ = 4 widehat { j } – 4 widehat { k } =( 0 , 4 , -4 ) $$

در نتیجه، اندازه بردار $$overrightarrow { c } $$  برابر است با:

$$|overrightarrow { c } = sqrt { 4^ 2 +  ( -4 )^ 2 } = sqrt { 32 } = 4 sqrt { 2 } $$

تابع برداری چیست؟

تا اینجا با تعریف کمیت برداری و مهم‌ترین ویژگی‌های آن‌ها آشنا شدیم. در این بخش با مفهومی به نام تابع برداری آشنا می‌شویم. تابع برداری، دو ویژگی بسیار مهم دارد:

1. دامنه آن مجموعه‌ای از اعداد حقیقی هستند.
2. برد آن مجموعه‌ای از بردارها هستند.

بنابراین، توابع برداری را می‌توانیم گسترش یافته توابع عددی یا اسکالر در نظر بگیریم. با توجه به آن‌که بردارهای واحد $$widehat { i } $$ و $$widehat { j } $$ و $$widehat { k } $$ به ترتیب در راستای محورهای $$x $$ و $$ y $$ و $$ z $$ قرار گرفته‌اند، تابع برداری سه‌بعدی را می‌توانیم به دو صورت زیر بنویسیم:

$$overrightarrow{ r ( t ) } = x( t ) widehat{ i } + y ( t ) widehat { j } + z ( t ) widehat { k } \ overrightarrow{ r ( t ) } = ( x ( t ) , y ( t ) , z ( t ) ) $$

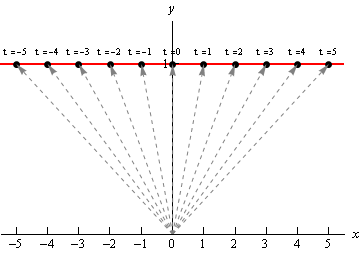
ورودی و خروجی تابع عددی، عدد است. اما تابع برداری، عدد را به عنوان ورودی می‌گیرد و برداری با اندازه و جهت مشخص، تحویل می‌دهد. فرض کنید تابع برداری $$overrightarrow { r ( t ) } $$ را به صورت $$overrightarrow { r ( t ) } = ( t , 1 ) $$ داریم. برای رسم این تابع برداری، مقدار $$overrightarrow { r ( t ) } $$ را به ازای مقدارهای مختلف t به‌دست می‌آوریم.

t	$$overrightarrow {  r ( t ) } $$
۳-	$$overrightarrow { r ( – 3 ) } = ( -3 , 1 ) $$
۱-	$$overrightarrow { r ( – 1 ) } = ( -1 , 1 ) $$
۲	$$overrightarrow { r (  2 ) } = ( 2 , 1 ) $$
۵	$$overrightarrow { r ( 5 ) } = ( 5 , 1 ) $$
۳	$$overrightarrow { r (  3 ) } = ( 3 , 1 ) $$
۱	$$overrightarrow { r (  1 ) } = ( 1 , 1 ) $$
۲-	$$overrightarrow { r (  -2 ) } = ( -2 , 1 ) $$

نقطه‌های داخل جدول، روی تابع برداری $$overrightarrow { r ( t ) } = ( t , 1 ) $$ قرار دارند. این تابع به صورت زیر رسم می‌شود. همان‌طور که در نمودار زیر مشاهده می‌کنید، ابتدا هر بردار، مبدا مختصات و انتهای آن، نقطه روی تابع برداری است.

تانسور چیست و چه رابطه ای با کمیت های برداری دارد؟

در بخش‌های قبل فهمیدیم کمیت برداری چیست و در مورد مهم‌ترین ویژگی‌های آن‌ها صحبت کردیم. در این بخش، به طور خلاصه تانسور را تعریف و رابطه آن با کمیت نرده‌ای و برداری را توضیح می‌دهیم. تانسورها، مانند کمیت‌های نرده‌ای و برداری، ابزارهای ریاضی هستند که از آن‌ها برای توصیف ویژگی‌های فیزیکی استفاده می‌شود. در حقیقت، تانسورها تعمیم یافته کمیت‌های برداری و اسکالر هستند. کمیت نرده‌ای، تانسور مرتبه صفر و بردار تانسور مرتبه یک است.

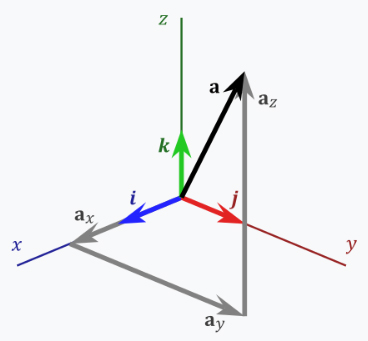
در بخش‌های قبل فهمیدیم هر کمیت برداری را می‌توانیم برحسب بردارهای پایه بنویسیم. تانسورها ابزارهای ریاضی هستند که با تغییر بردارهای پایه، به شکل ویژه‌ای منتقل می‌شوند. از تانسورها برای توصیف خمیدگی فضا زمان در نسبیت عام استفاده می‌کنیم. تانسور مرتبه اول، بردار نام دارد. فرض کنید برداری مانند $$overrightarrow { a } $$ با مولفه‌های $$a_x$$ در امتداد محور $$x$$ و $$a_y$$ در امتداد محور y و $$a_z$$ در امتداد محور z داریم. این بردار را برحسب بردارهای پایه به صورت زیر می‌نویسیم:

$$overrightarrow{ a } = a _x widehat{ i } + a_y widehat{ j } + a_z widehat{ k }$$

در حالت کلی، هر بردار را با تعداد بردارهای پایه در امتداد هر محور مختصات و جمع آن‌ها با یکدیگر توصیف می‌کنیم. اما راه دیگری نیز برای توصیف کمیت برداری برحسب بردارهای پایه وجود دارد. برای انجام این کار، حاصل ضرب داخلی بردار را با بردارهای پایه به‌دست می‌آوریم.

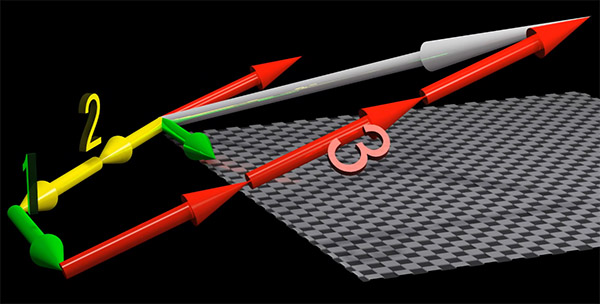
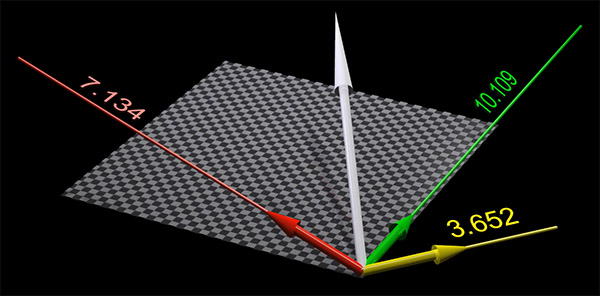
به جای بردارهای پایه $$widehat { i } $$ و $$widehat { j } $$ و $$widehat { k } $$، می‌توانیم بردارهای پایه جدیدی انتخاب کنیم. فرض کنید بردار $$overrightarrow { t } $$ با مولفه‌های ۴، ۲ و ۶ را در این پایه جدید داریم. همان‌طور که در تصویر زیر می‌بینید، هر یک از بردارهای زرد، سبز و قرمز،‌ یکی از بردارهای پایه را نشان می‌دهد.

فرض کنید طول هر بردار پایه (زرد،‌ سبز و قرمز) را به صورت نشان داده شده در تصویر زیر، دو برابر می‌کنیم.

پس از دو برابر کردن طول هر بردار پایه، مولفه‌های بردار $$overrightarrow { t } $$ برابر ۲، ۱ و ۳ می‌شوند. بنابراین، با افزایش طولِ بردارهای پایه، مولفه‌های بردار $$overrightarrow { t } $$ کاهش می‌یابند. از آنجا که طول بردارهای پایه و مقدار مولفه‌های بردار $$overrightarrow { t } $$ رابطه معکوسی با یکدیگر دارند. به آن‌ها مولفه‌های پادوردای بردار $$overrightarrow { t } $$ گفته می‌شود. توصیف کمیت برداری برحسب مولفه‌های پادوردا یکی از رایج‌ترین راه‌ها برای توصیف آن بردار است.

اکنون فرض کنید، به جای توصیف بردار به روش فوق، آن را برحسب ضرب نقطه‌ای با هر یک از بردارهای پایه توصیف کنیم. اگر طول بردارهای پایه برابر یک باشد، حاصل ضرب نقطه‌ای، برابر طول‌های نشان داده شده در تصویر زیر خواهد بود.

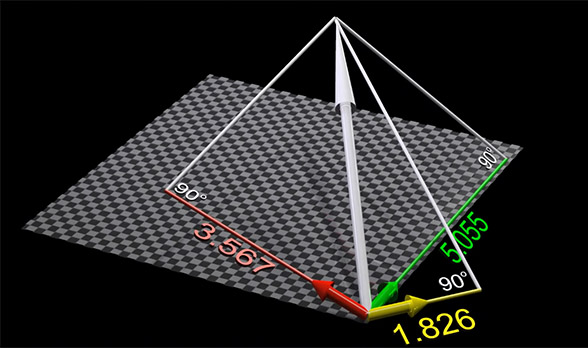
اگر طول بردارهای پایه در هر راستا دو برابر شود، حاصل ضرب داخلی بردار در هر بردار پایه نیز دو برابر خواهد شد.

اگر طول بردارهای پایه را کاهش دهیم، ضرب نقطه‌ای نیز کاهش می‌یابد. از آنجا که طول بردارهای پایه و مقدار مولفه‌های بردار $$overrightarrow { t } $$ متناسب با یکدیگر تغییر می‌کنند. به آن‌ها مولفه‌های هموردای بردار $$overrightarrow { t } $$ گفته می‌شود. متغیرهای مولفه‌های هموردا را می‌توانیم با اندیس زیر و متغیرهای پادوردار را با اندیس بالا به صورت زیر نشان دهیم:

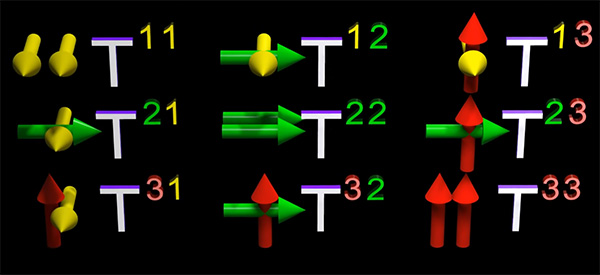
فرض کنید دو بردار متفاوت به نام‌های $$overrightarrow { V } $$ و $$overrightarrow { P }$$ داریم. یکی از مولفه‌های پادوردای بردار $$overrightarrow { V } $$ را در یکی از مولفه‌های پادوردای بردار $$overrightarrow { P } $$ ضرب می‌کنیم. با در نظر گرفتن تمام حالت‌های ممکن این ضرب، آن را می‌توانیم به شکل ماتریسی سه در سه بنویسیم:

$$begin{bmatrix} V^ {color { maro } { 1 } } P ^ {color { maro } { 1 } } & V^ {color { maro } { 1 } } P ^ {color { green } { 2 } } & V^ {color { maro } { 1 } } P ^ {color { red } { 3 } }\ V^ {color { green } { 2 } } P ^ {color { maro } { 1 } } & V^ {color { green } { 2 } } P ^ {color { green } { 2 } } & V^ {color { green } { 2 } } P ^ {color { red } { 3 } } \ V^ {color { red } { 3 } } P ^ {color { maro } { 1 } } & V^ {color { red } { 3 } } P ^ {color { green } { 2 } } & V^ {color { red } { 3 } } P ^ {color { red } { 3 } }end{bmatrix}$$

ماتریس‌ها مثالی از تانسور مرتبه دو هستند. اکنون فرض کنید مولفه‌های هموردای $$overrightarrow { V } $$ را با مولفه‌های پادوردای $$overrightarrow { P } $$ به صورت نشان داده شده در ادامه در یکدیگر ضرب می‌کنیم.

$$begin{bmatrix} V_ {color { maro } { 1 } } P ^ {color { maro } { 1 } } & V_ {color { maro } { 1 } } P ^ {color { green } { 2 } } & V_ {color { maro } { 1 } } P ^ {color { red } { 3 } }\ V_ {color { green } { 2 } } P ^ {color { maro } { 1 } } & V_ {color { green } { 2 } } P ^ {color { green } { 2 } } & V_ {color { green } { 2 } } P ^ {color { red } { 3 } } \ V_ {color { red } { 3 } } P ^ {color { maro } { 1 } } & V_ {color { red } { 3 } } P ^ {color { green } { 2 } } & V_ {color { red } { 3 } } P ^ {color { red } { 3 } }end{bmatrix}$$

در اینجا باز هم تانسور مرتبه دو با توصیفی متفاوت داریم. در ادامه، مولفه‌های هموردای $$overrightarrow { V } $$ را با مولفه‌های هموردای $$overrightarrow { P } $$ به صورت نشان داده شده در ادامه در یکدیگر ضرب می‌کنیم.

$$begin{bmatrix} V_ {color { maro } { 1 } } P _ {color { maro } { 1 } } & V_ {color { maro } { 1 } } P _ {color { green } { 2 } } & V_ {color { maro } { 1 } } P _ {color { red } { 3 } }\ V_ {color { green } { 2 } } P _ {color { maro } { 1 } } & V_ {color { green } { 2 } } P _ {color { green } { 2 } } & V_ {color { green } { 2 } } P _ {color { red } { 3 } } \ V_ {color { red } { 3 } } P _ {color { maro } { 1 } } & V_ {color { red } { 3 } } P _ {color { green } { 2 } } & V_ {color { red } { 3 } } P _ {color { red } { 3 } }end{bmatrix}$$

این حالت نیز توصیف دیگری از تانسور مرتبه دو را به ما می‌دهد. یکی از مهم‌ترین ویژگی‌های تانسور آن است که با تغییر بردارهای پایه، مولفه‌های آن به شیوه‌ای مشخص تغییر می‌کنند و ماهیت کلی تانسور (اسکالر بودن، بردار بودن، یا ماهیت پیچیده‌تر) حفظ خواهد شد. به این نکته توجه داشته باشید که تانسور حتما نباید با استفاده از مولفه‌های کمیت برداری ایجاد شود. همان‌طور که در ابتدای این بخش گفتیم بردار، تانسور مرتبه یک است. تانسور مرتبه یک یا همان بردار، در راستای هر محور مختصات برحسب ضریبی از بردار پایه نشان داده می‌شود. به بیان دیگر، بردار، مولفه‌ای در راستای هر یک از محورهای مختصات دارد.

در تانسور مرتبه دو، به جای دادن عدد به هر بردار پایه، عددی را با هر ترکیب ممکن از دو بردار پایه مرتبط می‌کنیم. به عبارت دیگر، در تانسور مرتبه ۲، به جای ماتریس $$1 times 1 $$ (برای اسکالر) یا $$1 times n$$ (برای بردار)، با ماتریسی $$n times  n $$ سروکار داریم. این موضوع را با مثالی ساده به صورت ملموس‌تر توضیح می‌دهیم. فرض کنید اتاقی داریم که کف آن به شکل صفحه شطرنج، از موزاییک‌های سیاه و سفید، تشکیل شده است. دماسنج نصب شده روی دیوار اتاق، دمای آن را ۲۱ درجه سانتی‌گراد نشان می‌دهد. دما کمیتی اسکالر یا نرده‌ای است و تنها با یک عدد، مشخص می‌شود.

پنجره باز است و نسیمی ملایم به داخل اتاق می‌وزد. نسیم، همان بردار است که شدت و جهت دارد. فرض کنید میز بزرگی داخل اتاق قرار دارد. این میز، همان تانسور مرتبه دو است که جفت موزاییک‌های مربع شکل کف اتاق (سیاه و سفید)‌ را دنبال می‌کند. میز ممکن است به شما بگوید اگر از بالاترین موزاییک، سمت چپ اتاق به پایین‌ترین موزاییکِ سمت راست اتاق بیایید، شیب اتاق چگونه تغییر می‌کند. همچنین، ممکن است اطلاعاتی در مورد فشاری که دو موزاییک مجاور به یکدیگر وارد می‌کنند، به شما بدهد. در این مثال، موزاییک‌های سیاه و سفید می‌توانند نقش بردارهای پایه را ایفا کنند.

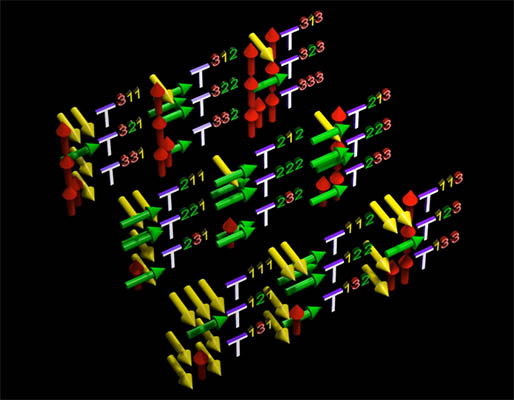
بار دیگر به فضای ساخته شده از بردارهای زرد، سبز و قرمز برمی‌گردیم. در تانسور مرتبه دو، تمام حالت‌های ممکن از ترکیب دو بردار از این سه بردار را در نظر می‌گیریم. تمام ترکیب‌های ممکن در تصویر زیر نشان داده شده‌اند.

در تانسور مرتبه سه، تمام حالت‌های ممکن از ترکیب سه بردار را در نظر می‌گیریم. به همین ترتیب، تانسور مرتبه n در m بعد، ابزاری ریاضی است که n اندیس و $$m ^ m $$ مولفه دارد و از قوانین انتقال مشخصی پیروی می‌کند.

جمع‌بندی

در این مطلب از مجله فرادرس، ابتدا فهمیدیم کمیت برداری چیست. سپس با تفاوت کمیت‌های اسکالر و برداری آشنا شدیم. به کمیت‌هایی که اندازه و جهت دارند، کمیت برداری گفته می‌شود. برای شناخت کمیت‌ برداری، باید اندازه و جهت آن را بدانیم و تنها با دانستن اندازه یا جهت، نمی‌توانیم کمیت‌های برداری را توصیف کنیم. پس از پاسخ به پرسش کمیت برداری چیست، در مورد جمع، تفریق و ضرب بردارها همراه با مثال‌های مختلف صحبت کردیم.