فرجه، یکی از اجزای اعداد رادیکالی است که در پشت رادیکال قرار می‌گیرد. اعداد رادیکالی از علامت رادیکال، مقدار زیر رادیکال و فرجه رادیکال (عدد پشت رادیکال) تشکیل می‌شوند. فرجه رادیکال، با عنوان ریشه نیز شناخته می‌شود. حل مسائل مرتبط با عبارت‌های رادیکالی و برخی از مسائل مرتبط با ریشه‌یابی، با استفاده از مفهوم فرجه صورت می‌گیرد. فرجه رادیکال به صورت پیش‌فرض و در اغلب موارد برابر با $$ ۲ $$ (جذر) در نظر گرفته می‌شود. بسیاری از قوانین رادیکال‌ها، به فرجه رادیکال ارتباط دارند. همین موضوع، اهمیت بالای یادگیری مفهوم فرجه و نحوه محاسبه آن را نمایش می‌دهد. در این آموزش از مجله فرادرس، بررسی می‌کنیم که فرجه رادیکال چیست و چگونه محاسبه می‌شود.

رادیکال و فرجه رادیکال چیست؟

عبارت رادیکالی، یک عبارت ریاضی است که با استفاده از علامت زیر نوشته می‌شود:

$$ sqrt { } $$

به علامت بالا، رادیکال می‌گویند. عدد زیر را در نظر بگیرید:

$$ sqrt { ۲ } $$

این عدد، یک عدد رادیکالی است که به صورت «رادیکال دو» خوانده می‌شود. عبارت زیر، فرم کلی اعداد رادیکالی و اجزای آن‌ها را نمایش می‌دهد:

$$ sqrt [ n ] { x } $$

• $$ sqrt { } $$: علامت رادیکال
• $$ x $$: عدد زیر رادیکال
• $$ n $$: فرجه رادیکال

عددی که پشت رادیکال قرار می‌گیرد (n)، به عنوان فرجه رادیکال در نظر گرفته می‌شود.

مثال ۱: تعیین فرجه رادیکال

فرجه اعداد رادیکالی زیر را مشخص کنید.

$$
begin {aligned} & sqrt [ ۶ ] { ۶۴ } \
& sqrt [ ۳ ] { ۲۷ } \
& sqrt { ۱۶ } \
end {aligned}
$$

برای مشخص کردن فرجه هر یک از اعداد رادیکالی بالا، به عدد پشت رادیکال نگاه می‌کنیم. در عدد اول ($$ sqrt [ ۶ ] { ۶۴ } $$)، عدد پشت رادیکال برابر با $$ ۶ $$، است. بنابراین فرجه این عدد رادیکالی برابر با ۶ می‌شود. در عدد دوم ($$ sqrt [ ۳ ] { ۲۷ } $$)، عدد پشت رادیکال یا همان فرجه رادیکال برابر با $$ ۳ $$ است. بر خلاف دو عدد اول، چیزی پشت رادیکال عدد سوم ($$ sqrt { ۱۶ } $$) نوشته نشده. اگر فرجه رادیکال مشخص نشده باشد، آن را برابر با $$ ۲ $$ در نظر می‌گیریم. به عبارت دیگر:

$$
sqrt { ۱۶ } = sqrt [ ۲ ] { ۱۶ }
$$

بنابراین، فرجه رادیکال در عدد سوم برابر با $$ ۲ $$ است.

مفهوم فرجه رادیکال چیست؟

برای درک مفهوم فرجه رادیکال، ابتدا مفهوم رادیکال و توان را مرور می‌کنیم. عدد توان‌دار زیر را در نظر بگیرید:

$$ ۳ ^ ۲ $$

بر اساس مفهوم اعداد توان‌دار، عدد بالا، ضرب دو عدد $$ ۳ $$ در یکدیگر را نمایش می‌دهد:

$$ ۳ ^ ۲ = ۳ times ۳ $$

حاصل $$ ۳ $$ به توان $$ ۲ $$ برابر با $$ ۹ $$ است.

$$ ۲ ^ ۲ = ۳ times ۳  = ۹ $$

اگر عدد $$ ۳ $$ به توان $$ ۳ $$ می‌رسید ($$ ۲ ^ ۳ $$)، حاصل آن از ضرب سه عدد $$ ۳ $$ به دست می‌آمد:

$$ ۳ ^ ۳ = ۳ times ۳ times ۳ $$

$$ ۳ ^ ۳ = ۳ times ۳ times ۳ = ۲۷ $$

اکنون، عدد رادیکالی زیر را در نظر بگیرید:

$$ sqrt { ۹ } $$

این عدد، رادیکال $$ ۹ $$ با فرجه $$ ۲ $$ (فرجه نوشته نشده) است. مفهوم رادیکال، عکس مفهوم توان است. برای به دست آوردن عدد بالا بر اساس مفهوم رادیکال، به دنبال عددی می‌گردیم که اگر آن را $$ ۲ $$ بار (به اندازه فرجه رادیکال) در خودش ضرب کنیم، به عدد $$ ۹ $$ (مقدار زیر رادیکال) برسیم. جواب ما، عدد $$ ۳ $$ خواهد بود. زیرا:

$$ ۳ times ۳  = ۹ $$

بنابراین:

$$ sqrt [ ۲ ] { ۹ } = ۳ $$

در نتیجه می‌توانیم بگوییم که فرجه یک عدد رادیکالی، توانِ یک عدد توان‌دار است که حاصل آن برابر با مقدار زیر رادیکال می‌شود.

$$ sqrt [ ۲ ] { ۳ ^ ۲ } = ۳ $$

همان‌طور که مشاهده می‌کنید، اگر جواب رادیکال را به توان فرجه برسانیم، به مقدار زیر رادیکال می‌رسیم. فرم کلی رابطه بین یک عدد رادیکالی با معادل توانی آن به صورت زیر به نوشته می‌شود:

$$ sqrt [ n ] { a } = a ^ { frac { ۱ } { n } } $$

بر اساس این رابطه، می‌توانیم بگوییم مفهوم فرجه، برعکس توان است. به عنوان مثال، اگر عدد $$ ۴ $$ را به توان $$ ۳ $$ برسانیم، جواب آن برابر با $$ ۶۴ $$ می‌شود. در طرف مقابل، با محاسبه رادیکال عدد $$ ۶۴ $$ با فرجه $$ ۳ $$، به عدد $$ ۴ $$ می‌رسیم.

مثال ۲: محاسبه مقدار زیر رادیکال

با استفاده از مفهوم فرجه رادیکال، مقدار زیر رادیکال را به دست بیاورید.

$$
sqrt [ ۳ ] { ? } = ۵
$$

مقدار زیر رادیکال، برابر با جواب رادیکال به توان فرجه است:

$$ sqrt [ ۳ ] { ۵ ^ ۳ } = ۵ $$

بنابراین، داریم:

$$ ۵ ^ ۳ = ۱۲۵ $$

در نتیجه، مقدار زیر رادیکال برابر با $$ ۱۲۵ $$ است.

مثال ۳: نوشتن فرم توانی اعداد رادیکالی

اعداد رادیکالی زیر را به صورت اعداد توان‌دار بازنویسی کنید.

$$
begin {aligned} & sqrt [ ۴ ] { ۱۶ } \
& sqrt [ ۱۰ ] { ۸ x } \
& sqrt {x ^ ۲ + y ^ ۲ } \
end {aligned}
$$

برای نوشتن فرم توانی اعداد رادیکالی، مقدار زیر را رادیکال را به عنوان پایه و حاصل تقسیم توان این مقدار بر فرجه رادیکال را به عنوان توان در نظر می‌گیریم. برای شروع، عدد رادیکالی $$ sqrt [ ۴ ] { ۱۶ } $$ را در نظر بگیرید. اجزای مختلف این عدد عبارت هستند از:

• مقدار زیر رادیکال: $$ ۱۶ $$
• توان مقدار زیر رادیکال: $$ ۱ $$
• فرجه رادیکال: $$ ۴ $$
• حاصل تقسیم توان مقدار زیر رادیکال بر فرجه زیر رادیکال: $$ frac { ۱ } { ۴ } $$

با توجه به این اطلاعات، داریم:

$$ sqrt [ ۴ ] { ۱۶ ^ ۱ } = ۱۶ ^ { frac { ۱ } { ۴ } } $$

به این ترتیب، برای عبارت $$ sqrt [ ۱۰ ] { ۸ x } $$ خواهیم داشت:

• مقدار زیر رادیکال: $$ ۸ x $$
• توان مقدار زیر رادیکال: $$ ۱ $$
• فرجه رادیکال: $$ ۱۰ $$
• حاصل تقسیم توان مقدار زیر رادیکال بر فرجه زیر رادیکال: $$ frac { ۱ } { ۱۰ } $$

در نتیجه:

$$ sqrt [ ۱۰ ] { ( ۸ x ) ^ ۱ } = ( ۸ x ) ^ { frac { ۱ } { ۱۰ } } $$

به همین شکل، برای عبارت $$ sqrt {x ^ ۲ + y ^ ۲ } $$، داریم:

• مقدار زیر رادیکال: $$ x ^ ۲ + y ^ ۲ $$
• توان مقدار زیر رادیکال: $$ ۱ $$
• فرجه رادیکال: $$ ۲ $$
• حاصل تقسیم توان مقدار زیر رادیکال بر فرجه زیر رادیکال: $$ frac { ۱ } { ۲ } $$

بنابراین:

$$ sqrt { left ( x ^ ۲ + y ^ ۲ right ) ^ ۱} = left ( x ^ ۲ + y ^ ۲ right ) ^ { frac { ۱ }{ ۲ }} $$

در این مثال، می‌توانستیم جواب یکی از رادیکال‌‌ها را بدون انجام محاسبات پیچیده به دست بیاوریم. عدد $$ sqrt [ ۴ ] { ۱۶ } $$ را در نظر بگیرید. می‌دانیم که عدد $$ ۱۶ $$، با دو به توان چهار ($$ ۲ ^ ۴ $$) برابر است:

$$ ۲ ^ ۴ = ۲ times ۲ times ۲ times ۲ = ۱۶ $$

بنابراین، می‌توانیم فرم توانی $$ sqrt [ ۴ ] { ۱۶ } $$ را به صورت زیر بنویسیم:

$$ sqrt [ ۴ ] { ۱۶ } = sqrt [ ۴ ] { ۲ ^ ۴ } = ۲ ^ { frac { ۴ } { ۴ } } $$

$$ sqrt [ ۴ ] { ۱۶ } = ۲ ^ { frac { ۴ } { ۴ } } = ۲ ^ ۱ $$

$$ sqrt [ ۴ ] { ۱۶ } = ۲ $$

در نتیجه، جواب $$ sqrt [ ۴ ] { ۱۶ } $$ برابر با $$ ۲ $$ است. نکته‌ای که به آن اشاره کردیم، در اغلب موارد برای ساده‌سازی عبارت‌های زیر رادیکال در مسائل مختلف ریاضی مورد استفاده قرار می‌گیرد. در ادامه این مطلب از مجله فرادرس، می‌خواهیم ببینیم رابطه بین ریشه و فرجه رادیکال چیست.

چگونه مفهوم رادیکال و فرجه رادیکال را یاد بگیریم؟

رادیکال و انجام محاسبات ریاضی بر روی عبارت‌های رادیکالی، از مباحث مهمی هستند که دانش‌آموزان در دوره متوسط اول با آشنا می‌شوند و در صورت ادامه تحصیل در رشته‌های فنی و مهندسی، در دوره‌های مختلف با آن‌ها برخورد می‌کنند. ساده‌ترین راه برای یادگیری مفهوم رادیکال و فرجه رادیکال، مطالعه مباحث پایه‌ای مطرح شده در کتاب‌های ریاضی دوره متوسطه اول و دوم است. البته برای یادگیری این موضوع به بهترین شکل، نیاز به توضیحات واضح و حل مثال‌ها و تمرین‌های متنوع دارید. فیلم‌های آموزش ریاضی دوره متوسط اول فرادرس، تمام نیازهای شما برای آشنایی با مباحث ریاضی دبیرستان را برطرف می‌کنند. عنوان دوره‌های مرتبط فرادرس در زمینه موضوع رادیکال و فرجه رادیکال در ادامه آورده شده‌اند:

علاوه بر دوره‌های بالا، فرادرس، فیلم‌های آموزشی دیگری را در زمینه دیگر دروس دوره‌های متوسطه اول و دوم تهیه کرده است که در صورت تمایل می‌توانید عنوان درس مورد نظر خود را از میان آن‌ها پیدا کنید و به یادگیری بهتر درس‌های خود بپردازید. لینک این دوره‌ها در ادامه آورده شده است.

رابطه بین ریشه و فرجه رادیکال چیست؟

ریشه و فرجه رادیکال، دو مفهوم مشابه در ریاضیات هستند. البته کاربردها و در برخی از موارد، خروجی آن‌ها با یکدیگر تفاوت دارد. برای درک مفهوم ریشه، معادله درجه دو زیر را در نظر بگیرید:

$$ x ^ ۲ – ۴ = ۰ $$

برای به دست آوردن جواب این معادله، به صورت زیر عمل می‌کنیم:

$$ x ^ ۲ = ۴ $$

$$ sqrt { x ^ ۲ } = sqrt { ۴ } $$

$$ x = pm ۲ $$

طی مراحل بالا، ریشه‌های دوم متغیر $$ x $$ را به دست آوردیم. این ریشه‌ها برابر با $$ + ۲ $$ و $$ – ۲ $$ هستند. احتمالا برایتان این سوال برایتان پیش می‌آید که مگر خروجی رادیکال با فرجه زوج (در اینجا فرجه $$ ۲ $$)، نباید عددی مثبت یا $$ ۰ $$ باشد؛ پس چرا جواب $$ sqrt { ۴ } $$ برابر با $$ + ۲ $$ و $$ – ۲ $$ شد. جواب این سوال، در مفهوم ریشه و توان نهفته است.

ریشه‌ی عددی مانند $$ a $$، هر عددی است که با رساندن آن به یک توان مشخص، به $$ a $$ برسیم. در اینجا، $$ + ۲ $$ و $$ – ۲ $$، ریشه‌های دوم عدد $$ ۴ $$ هستند. زیرا با رساندن هر یک از آن‌ها به توان دو، به $$ ۴ $$ می‌رسیم:

$$ ( + ۲ ) ^ ۲ = ۴ $$

$$ ( – ۲ ) ^ ۲ = ۴ $$

اکنون، $$ sqrt { ۴ } $$ را به تنهایی و خارج از فرآیند حل معادله در نظر بگیرید. جواب این رادیکال، عبارت است از:

$$ sqrt [ ۲ ] { ۴ } = sqrt [ ۲ ] { ۲ ^ ۲ } = ۲ ^ { frac { ۲ } { ۲ } } = ۲ ^ ۱ = ۲ $$

جواب $$ sqrt { ۴ } $$، برابر با $$ + ۲ $$ است. این جواب، تنها یکی از ریشه‌های عدد $$ ۴ $$ را نمایش می‌دهد. پس عدد چهاری که می‌خواهیم از آن رادیکال بگیریم و عدد چهاری که از به توان دو رساندن $$ + ۲ $$ یا $$ – ۲ $$ به دست می‌آید، از نظر ماهیت با یکدیگر تفاوت دارند. یکی از آن‌ها طی فرآیند ضرب توانی به دست می‌آید و دیگری از ابتدا زیر رادیکال قرار دارد.

برای رفع ابهام در مبحث تفاوت بین مفهوم ریشه و فرجه رادیکال، از عبارت «ریشه اصلی» (Principal Root) برای فرجه رادیکال استفاده می‌شود. بر این اساس، ریشه اصلی عدد $$ ۴ $$ برابر با $$ + ۲ $$ خواهد بود. عدد $$ – ۲ $$، به عنوان ریشه فرعی عدد $$ ۴ $$ معرفی می‌شود.

برای رادیکال با فرجه فرد، مقدار زیر رادیکال می‌تواند هر مقدار حقیقی (مثبت، صفر یا منفی) باشد. در این حالت، تفاوتی بین جواب رادیکال یک عدد با فرجه فرد و ریشه فرد همان عدد وجود ندارد. به عنوان مثال، $$ sqrt [۳] { – ۸ } $$ را در نظر بگیرید. جواب این رادیکال برابر است با:

$$ sqrt [۳] { – ۸ }  = sqrt [۳] { ( – ۲ ) ^ ۳ } = ( – ۲ ) ^ {frac { ۳ } { ۳ } } = – ۲ $$

اکنون، ریشه سوم عدد $$ – ۸ $$ را در نظر بگیرید. ریشه سوم این عدد، همان $$ – ۲ $$ می‌شود. زیرا:

$$ ( – ۲ ) ^ ۳ = ( – ۲ ) ( – ۲ ) ( – ۲ ) = – ۸ $$

قوانین فرجه رادیکال چیست؟

در بخش قبلی دیدیم که جواب رادیکال با فرجه زوج، همواره غیرمنفی (مثبت یا صفر) است. به علاوه، جواب رادیکال با فرجه فرد، می‌تواند مثبت، صفر یا منفی باشد.

در این بخش، به معرفی دیگر قوانین مرتبط با فرجه رادیکال می‌پردازیم. این قوانین عبارت هستند از:

$$ sqrt [ n ] { a ^ m } = a ^ { frac { m } { n } } $$

$$ sqrt [ n ] { a ^ n } = a $$

$$ sqrt [ n ] { { a b } } = sqrt [ n ] { a } ,sqrt [ n ] { b } $$

$$ sqrt [ n ] { { frac { a } { b } } } = frac { { sqrt [ n ] { a } } } { { sqrt [ n ] { b } } } $$

$$
{ a ^ { frac { m } { n } } } = { left ( { { a ^ { frac { ۱ } { n } } } } right ) ^ m } = { left ( { sqrt [ n ] { a } } right ) ^ m } OR { a ^ { frac { m } { n } } } = { left ( { { a ^ m } } right ) ^ { frac { ۱ } { n } } } = sqrt [ n ] { { { a ^ m } } }
$$

$$
c sqrt [ n ] { a } pm c sqrt [ n ] { b } = c left ( sqrt [ n ] { a } pm sqrt [ n ] { b } right )
$$

مثال ۴: ساده سازی عبارت های رادیکالی

عبارت‌های رادیکالی زیر را با استفاده از قوانین فرجه رادیکال، ساده‌سازی کنید.

$$ sqrt { { y ^ ۷ } } $$

$$ sqrt [ ۹ ] { {  { x ^ ۶ } }  } $$

$$ sqrt { ۱۸ { x ^ ۶ } { y ^ { ۱۱ } } } $$

$$ sqrt [ ۵ ] { { frac { ۲ } { { { x ^ ۳ } } } } } $$

برای شروع، $$ sqrt { { y ^ ۷ } } $$ را در نظر بگیرید. به منظور ساده‌سازی این رادیکال، ابتدا مقدار زیر رادیکال را به صورت زیر بازنویسی می‌کنیم:

$$ y ^ ۷ = y ^ ۶ y = left ( y ^ ۳ right ) ^ ۲ y $$

به این ترتیب، داریم:

$$ sqrt { { y ^ ۷ } } = sqrt { left ( y ^ ۳ right ) ^ ۲ y } $$

عبارت‌های $$ left ( y ^ ۳ right ) ^ ۲ $$ و $$ y $$ را به عنوان دو عبارت مجزا در نظر می‌گیریم و از قانون زیر برای ساده‌سازی رادیکال استفاده می‌کنیم:

$$ sqrt [ n ] { { a b } } = sqrt [ n ] { a } ,sqrt [ n ] { b } $$

$$ a = left ( y ^ ۳ right ) ^ ۲ $$

$$ b = y $$

$$
sqrt { left ( y ^ ۳ right ) ^ ۲ y } = sqrt { left ( y ^ ۳ right ) ^ ۲ } sqrt { y }
$$

فرجه رادیکال‌های بالا برابر با $$ ۲ $$ است. بر اساس قانون زیر، می‌توانیم رادیکال اول را ساده کنیم:

$$ sqrt [ n ] { a ^ n } = a $$

$$
sqrt [ ۲ ] { left ( y ^ ۳ right ) ^ ۲ } = y ^ ۳
$$

بنابراین، داریم:

$$
sqrt { left ( y ^ ۳ right ) ^ ۲ y } = y ^ ۳ sqrt { y }
$$

در نتیجه:

$$
sqrt { y ^ ۷ } = y ^ ۳ sqrt { y }
$$

اکنون، به سراغ ساده‌سازی $$ sqrt [ ۹ ] { {  { x ^ ۶ } }  } $$ می‌رویم. بر اساس قانون زیر، فرم توانی رادیکال را می‌نویسیم:

$$ sqrt [ n ] { a ^ m } = a ^ { frac { m } { n } } $$

$$ a = x $$

$$ n = ۹ $$

$$ m = ۶ $$

$$
sqrt [ ۹ ] { { { x ^ ۶ } } } = x ^ { frac { ۶ } { ۹ } }
$$

در مرحله بعد، توان کسری را ساده می‌کنیم:

$$
x ^ { frac { ۶ } { ۹ } } = x ^ { frac { ۲ } { ۳ } }
$$

اکنون، فرم رادیکالی عدد توان‌دار بالا را می‌نویسیسم:

$$ a = x $$

$$ n = ۳ $$

$$ m = ۲ $$

$$
x ^ { frac { ۲ } { ۳ } } = sqrt [ ۳ ] { { { x ^ ۲ } }}
$$

برای ساده‌سازی $$ sqrt { ۱۸ { x ^ ۶ } { y ^ { ۱۱ } } } $$، ابتدا عبارت زیر رادیکال را به شکل زیر درمی‌آوریم:

$$
۱۸ { x ^ ۶} { y ^ { ۱۱ } } = ۹ { x ^ ۶ } { y ^ { ۱۰ } } left ( { ۲ y } right ) = ۹ { left ( { { x ^ ۳ } } right ) ^ ۲ } { left ( { { y ^ ۵ } } right ) ^ ۲ } left ( { ۲ y } right)
$$

سپس، عبارت تغییریافته را زیر رادیکال قرار می‌دهیم و آن را با استفاده از قوانین رادیکال، ساده می‌کنیم:

$$ sqrt { ۱۸ { x ^ ۶ } { y ^ { ۱۱ } } } = sqrt { ۹ { { left ( { { x ^ ۳ } } right ) } ^ ۲ } { { left( { { y ^ ۵ } } right ) } ^ ۲ } left( { ۲ y } right ) } $$

$$ sqrt { ۹ { { left ( { { x ^ ۳ } } right ) } ^ ۲ } { { left( { { y ^ ۵ } } right ) } ^ ۲ } left( { ۲ y } right ) } = sqrt ۹ sqrt { { { left( { { x ^ ۳ } } right ) } ^ ۲ } } sqrt { { { left ( { { y ^ ۵ }} right ) }^ ۲ } } sqrt { ۲ y } $$

$$
sqrt ۹ sqrt { { { left( { { x ^ ۳ } } right ) } ^ ۲ } } sqrt { { { left ( { { y ^ ۵ }} right ) }^ ۲ } } sqrt { ۲ y } = ۳ { x ^ ۳ } { y ^ ۵ } sqrt { ۲ y }
$$

$$
sqrt { ۱۸ { x ^ ۶ } { y ^ { ۱۱ } } } = ۳ { x ^ ۳ } { y ^ ۵ } sqrt { ۲ y }
$$

به منظور ساده‌سازی $$ sqrt [ ۵ ] { { frac { ۲ } { { { x ^ ۳ } } } } } $$، از قانون زیر استفاده می‌کنیم:

$$
sqrt [ n ] { { frac { a } { b } } } = frac { { sqrt [ n ] { a } } } { { sqrt [ n ] { b } } }
$$

$$ a = ۲ $$

$$ b = x ^ ۳ $$

$$ n = ۵ $$

$$
sqrt [ ۵ ] { { frac { ۲ } { { { x ^ ۳ } } } } } = frac { { sqrt [ ۵ ] { ۲ } } } { { sqrt [ n ] { x ^ ۳ } } }
$$

در مرحله بعد، صورت و مخرج عبارت را در $$ sqrt [ ۵ ] { x ^ ۲ } $$ ضرب می‌کنیم و ساده‌سازی را ادامه می‌دهیم:

$$
sqrt [ ۵ ] { { frac { ۲ } { { { x ^ ۳ } } } } } = frac { { sqrt [ ۵ ] { ۲ } } } { { sqrt [ ۵ ] { { { x ^ ۳ } } } } } frac { { sqrt [ ۵ ] { { { x ^ ۲ } } } } } { { sqrt [ ۵ ] { { { x ^ ۲ } } } } } = frac { { sqrt [ ۵ ] { { ۲ { x ^ ۲ } } } } } { { sqrt [ ۵ ] { { { x ^ ۵ } } } } } = frac { { sqrt [ ۵ ] { { ۲ { x ^ ۲ } } } } } { x }
$$

روش محاسبه فرجه رادیکال چیست؟

فرجه رادیکال با استفاده از قوانین رادیکال و اعداد توان‌دار محاسبه می‌شود. برای آشنایی با روند محاسبه فرجه رادیکال، به مثالی که در ادامه آورده‌ایم توجه کنید.

مثال ۵: تعیین فرجه رادیکال

فرجه رادیکال در $$ sqrt [ n ] { ۶۴ } = ۲ $$ را محاسبه کنید.

برای به دست آوردن فرجه $$ sqrt [ n ] { ۶۴ } $$ (پارامتر $$ n $$)، ابتدا فرم توانی رادیکال را می‌نویسیم:

$$ sqrt [ n ] { ۶۴ } = ۶۴ ^ { frac { ۱ } { n } } $$

بر اساس صورت مسئله، داریم:

$$
sqrt [ n ] { ۶۴ } = ۲ to ۶۴ ^ { frac { ۱ } { n } } = ۲
$$

اکنون، هر دو طرف مساوی را به توان $$ n $$ می‌رسانیم:

$$
left ( ۶۴ ^ { frac { ۱ } { n } } right ) ^ n = ۲ ^ n
$$

$$
۶۴ ^ { frac { n } { n } }= ۲ ^ n
$$

$$
۶۴ ^ { ۱ }= ۲ ^ n
$$

$$
۶۴ = ۲ ^ n
$$

همان‌طور که مشاهده می‌کنید، عدد $$ ۲ $$ به توان یک عدد دیگر ($$ n $$) برابر با $$ ۶۴ $$ شده است. بر اساس این رابطه، عددی که دنبال آن می‌گردیم، $$ ۶ $$ است. چراکه:

$$ ۲ ^ ۶ = ۶۴ $$

$$ ۲ ^ ۶ = ۲ ^ n $$

$$ n = ۶ $$

فرجه رادیکال در ماشین حساب + نرم افزارهای آفلاین و آنلاین

در اغلب ماشین‌حساب‌ها، گزینه‌ای وجود دارد که امکان محاسبه رادیکال اعداد را فراهم می‌کند. فرجه رادیکال در این محاسبات، معمولا برابر با $$ ۲ $$‌ است. اگر بخواهیم رادیکال با فرجه $$ ۳ $$ و بالاتر را به دست بیاوریم، باید از ماشین‌حساب‌های مهندسی و دکمه‌های مخصوص آن‌ها استفاده کنیم.

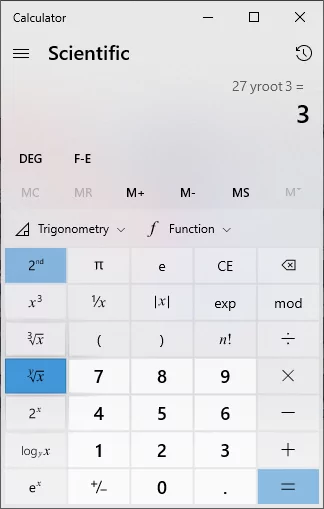
تصویر زیر، دکمه‌های مورد استفاده برای محاسبه رادیکال با فرجه $$ ۳ $$ و بالاتر در یک ماشین‌حساب مهندسی را نمایش می‌دهد.

در ماشین‌حساب ویندوز، گزینه «$$ sqrt [ y ] { x } $$»، امکان محاسبه رادیکال با فرجه $$ ۳ $$ و بالاتر را فراهم می‌کند. برای این کار، کافی است ابتدا مقدار زیر رادیکال را وارد کرده و پس از انتخاب دکمه مذکور، فرجه رادیکال را تایپ کنید. در انتها و با انتخاب دکمه مساوی ($$ = $$)، جواب رادیکال نمایش داده می‌شود.

نوشتن فرجه رادیکال در نرم‌افزار اکسل، با استفاده از قانون زیر انجام می‌گیرد:

$$ sqrt [ n ] { a ^ m } = a ^ { frac { m } { n } } $$

به عنوان مثال، فرمول $$ sqrt [ 4 ] { 3 } $$ در اکسل، به صورت زیر نوشته می‌شود:

= 3^(1/4)

فرجه رادیکال در فرمول‌های لتک (Latex) درون براکت ($$ [ ] $$) نوشته می‌شود. به عنوان مثال، کد زیر، فرمول $$ sqrt [ 3 ] { 2 } $$ را نمایش می‌دهد.

sqrt [ 3 ] { 2 }

در ماشین‌حساب‌های آنلاین و ابزارهای حل مسائل ریاضی با هوش مصنوعی نیز می‌توان با استفاده از یک یا تمام روش‌های بالا، جواب رادیکال با فرجه‌های مختلف را به دست آورد.

آزمون سنجش یادگیری فرجه رادیکال

در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث فرجه رادیکال را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.