در واقعیت امکان تشخیص مکان و مسیر دقیق حرکت الکترون در اتم وجود ندارد، مانند پرههای یک پنکه روشن که قادر به تشخیص و تفکیک آنها از هم نیستیم. بنابراین نیاز به استفاده از مفاهیم جدیدی در فیزیک وجود داشت. «نیلز بور» (Niels Bohr) این شرایط را به کاربرد زبان ولی در قالب شعر تشبیه کرد و «مدل کوانتومی اتم» (Quantum Model of Atom) همان زبان شعرگونه فیزیک است. در مدل کوانتومی اتم، الکترون دارای مقادیر انرژی معینی است اما در مورد مکان دقیق قرارگیری الکترون، با احتمال صحبت میشود. طبق پیشبینی این مدل، بیشترین احتمال حضور الکترونها در فضایی شبیه ابر به نام اوربیتال اتمی است.
در این مطلب از مجله فرادرس ابتدا بررسی میکنیم چگونه مشکلات مدل نیمهکلاسیکی بور، منجر به استفاده از مفاهیم کوانتومی و توسعه این مدل شد. سپس یاد میگیریم که مدل کوانتومی اتم چیست و در انتها با سایر مدلهای اتمی که برای مطالعه ساختار اتم پیشنهاد شدند، آشنا میشویم.
مدل کوانتومی اتم چیست؟
در مدل کوانتومی اتم، الکترونها بهصورت یک ابر سه بعدی دور هسته در نظر گرفته میشوند. این مدل توسط «اروین شرودینگر» (Erwin Schrödinger) و بر پایه رفتار موجگونه الکترون مطرح شد. در این مدل الکترون دور هسته نمیچرخد، بلکه مانند یک مه هسته را احاطه کرده است. مقدار دقیق انرژی و موقعیت احتمالی الکترون در اتم توسط کمیتی به نام تابعموج محاسبه میشود که حاوی اطلاعات مهمی مثل اعداد کوانتومی است. با استخراج این اطلاعات به کمک مکانیک کوانتوم، میتوانیم اوربیتالهای مختلفی که الکترون در آنها قرار دارد را شناسایی کنیم.
در تمام مدلهای اتمی که قبل از مدل کوانتومی اتم ارائه شدند، همیشه الکترون یک ذره در نظر گرفته میشد. اما واقعیت این است که وقتی الکترون در ابعادی مانند فضای داخل یک اتم قرار بگیرد، میتواند مانند یک موج رفتار کند. رفتار موجگونه الکترون، ایده اولیه کشف مدل کوانتومی اتم بود. بنابراین مدل کوانتومی اتم با در نظر گرفتن خاصیت موجی الکترون، مطالعه ساختار اتم را وارد دنیای جدیدی کرد. همچنین مقادیر مجاز و دقیق انرژی الکترون، جوابهایی هستند که با حل «معادله موج شرودینگر» (Schrödinger Wave Equation) در این مدل بدست میآیند.
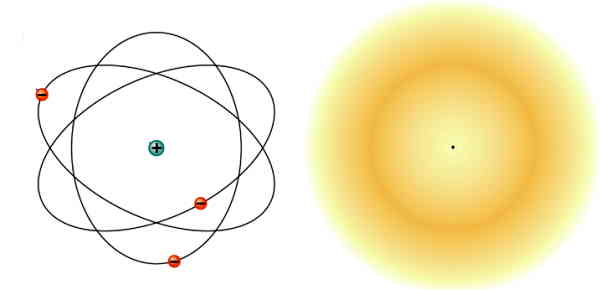
همانطور که در شکل مشخص است، در مدل ذرهای الکترونها بهصورت ذرات مشخصی در مدارهایی دور هسته در حال چرخشاند. در سمت راست شکل، نمایش ابر الکترونی بهخوبی موجی بودن الکترون در مدل کوانتومی را نشان میدهد. به همین دلیل، این مدل را «مدل ابر الکترون» (Electron Cloud Model) هم مینامند.
همچنین «مدل مکانیک کوانتومی اتم» (Quantum Mechanical Model of Atom)، «مدل مکانیک موجی اتم» (wave Mechanical Model of Atom) یا «مدل اتمی شرودینگر» (Schrödinger Atomic Model) دیگر نامهایی است که برای مدل کوانتومی اتم بکار میرود.
مدل اتم هیدروژن بور
در سال ۱۹۱۳، یک فیزیکدان دانمارکی به نام نیلز بور برای اولین بار با بررسی تابش گسیل شده توسط عناصر مختلف، خطوطی مجزا و تفکیک شده را مشاهده کرد. همانطور که گفتیم، پیش از بور مدلهای مختلفی برای اتم پیشنهاد شد و بور هم مدل خود را بر اساس آنها ساخت. در مدل بور الکترونها در مسیر دایرهای مشخصی به نام «مدار» (Orbit) در حال چرخش دور هستهاند، مانند حلقههای سیاره زحل که همواره در حال چرخش دور آن هستند.

او به دلیل همین شباهت، مدل خود را «مدل سیارهای» (Planetary Model) نامید. اما سوالهای زیر در مورد این مدل مطرح شد:
- الکترونها دقیقا کجا هستند و چه میکنند؟
- طبق پیشبینیهای فیزیک کلاسیک، چرا الکترونهای در حال چرخش دور هسته به سمت آن سقوط نمیکنند؟
- چنین ساختاری با خطوط تابشی از عناصر برانگیخته چه ارتباطی دارد؟
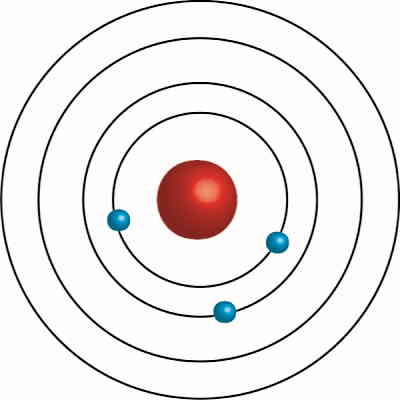
بور مشکلات بالا را با مفهوم «کمیت کوانتیده» (Quantized Quantity) و استفاده از «نظریه کوانتیزیشن پلانک» (Planck’s Theory of Quantization) حل کرد و مدل اتم هیدروژن خود را ارائه داد. در ادامه این بخش راجعبه این دو مبحث توضیح میدهیم. در واقع مشاهده طیف خطی تابش شده از عناصر مختلف، باعث شد تا بور به این فکر کند شاید الکترونها فقط در شعاعها یا انرژیهای خاصی درون اتم قرار میگیرند. پس او فرض کرد برای مدار حرکت الکترون و انرژی آن، فقط مقادیر مشخصی در نظر گرفته شود.
به این ترتیب بور مدل اتمی خود را فقط برای اتم هیدروژن و بر اساس کوانتیزیشن ارائه کرد. مدل اتم هیدروژن بور را میتوانیم در دو بخش خلاصه کنیم:
- الکترونهای در حال چرخش دور هسته فقط در مدارهایی با مقادیر شعاعی مشخص قرار دارند.
- الکترونهای در حال چرخش دور هسته دارای مقادیر انرژی مشخصی هستند.
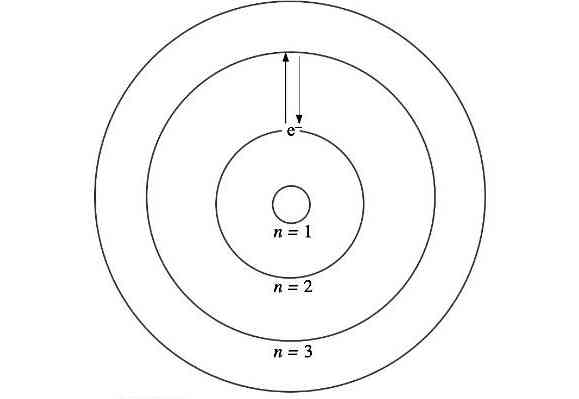
مقادیر مجاز شعاعی برای بخش اول از رابطه زیر محاسبه میشوند:
$$r(n) = n^2 r(1)$$
در این رابطه n یک عدد مثبت و صحیح است. همچنین r(1) شعاع بور نامیده میشود و معادل کوچکترین شعاع مجاز برای اتم هیدروژن با مقدار ۰٫۵۲۹×۱۰-۱۰ m است. بنابراین الکترونها فقط در مدارهایی با این شعاعها مجاز به حرکتاند و بین این مدارها یا هر جای دیگری از اتم، الکترون نمیتواند وجود داشته باشد.
با این فرض برای حرکت الکترونها، بور توانست انرژی هر الکترون در مدار nام برای اتم هیدروژن را نیز کوانتیزه کند. او مقادیر انرژی مجاز برای الکترونها را بهصورت زیر بدست آورد:
$$E(n) = – frac{13.6 eV}{n^2}$$
با توجه به این رابطه میتوانیم نتیجه بگیریم که انرژی هر الکترون به شعاع مداری بستگی دارد که در آن قرار دارد. کمترین انرژی برای الکترونی است که در کوچکترین مدار قرار دارد که در واقع نزدیکترین الکترون به هسته هم محسوب میشود.
ممکن است این سوال مطرح شود که چرا در رابطه E(n) مقدار انرژی منفی میشود. علت این است که انرژی الکترون در یک مدار را نسبت به انرژی الکترونی که کاملا از اتم جدا شده است، میسنجیم. انرژی الکترونی که کاملا از اتم جدا شده است، صفر است و برای آن n بهصورت بینهایت تعریف میشود. پس الکترونهای روی مدارهای اتم، باید مقدار انرژی منفی داشته باشند. در ادامه خواهیم دید مدل اتم هیدروژن بور چگونه میتواند فرآیندهای جذب و گسیل فوتون، طیف اتمی و نحوه قرارگیری الکترونها در لایههای اصلی را توضیح دهد. البته پیشتر در مطالب قبلی مجله فرادرس، به طور کامل راجع به نظریه اتمی صحبت کردیم که مطلب مربوطه را میتوانید از لینک زیر مطالعه کنید.
کمیت کوانتیده چیست؟
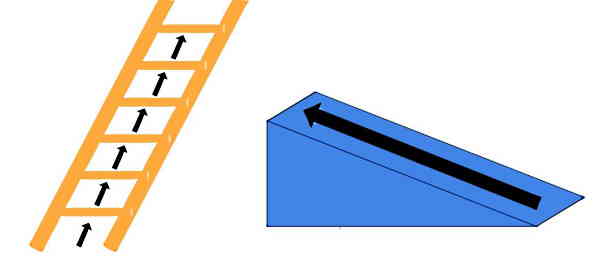
ابتدا باید بدانیم یک کمیت کوانتیده چه تعریفی دارد. وقتی یک کمیت کوانتیده است، یعنی فقط مقادیر مشخص و تفکیکشدهای میگیرد. درست شبیه زمانی که پیانو مینوازید. هر کلید در پیانو برای نت خاصی تنظیم شده است و شما فقط میتوانید برای مثال نتهای F یا F شارپ را بنوازید. اما نمیتوانید نتی بین F و F شارپ تولید کنید. بنابراین مفهوم «کوانتیزیشن» (Quantization) بر اساس کار کردن با کمیتهای کوانتیده شکل میگیرد. در شکل زیر میتوانید خیلی بهتر مفهوم کوانتیدگی یا پلهای بودن را در مقابل مفهوم پیوستگی درک کنید.
یک مثال مهم دیگر برای مفهوم کوانتیزیشن، طیف اتمی است. زمانی که یک عنصر یا یون بر اثر دریافت گرما یا جریان الکتریکی برانگیخته میشود، اتمهای برانگیخته شده نوری را گسیل میکنند که دارای مشخصه رنگی خاصی است. این نور را میتوانیم به وسیله یک منشور منعکس کنیم و در نتیجه طیفی حاصل میشود که دارای ظاهری تفکیک شده است. علت این امر آن است که فقط طولموجهای خاصی از نور گسیل شدهاند. در بخشهای بعدی راجعبه این مبحث بیشتر توضیح خواهیم داد.
نظریه پلانک
اوایل قرن بیستم بود که شاخهای جدید از علم فیزیک به نام «مکانیک کوانتومی» پایهگذاری شد. دانشمندانی مانند «ماکس پلانک» (Max Planck) و «آلبرت انیشتین» (Albert Einstein) متوجه شدند که تابش الکترومغناطیسی مانند نور فقط جنبه موجگونه ندارد، بلکه ماهیت ذرهای هم دارد. آنها این ذرات را «فوتون» (Photon) نامیدند.

پلانک به مطالعه تابش امواج الکترومغناطیسی از اجسام گرم شده پرداخت. او مشاهده کرد انرژی این تابش فقط مقادیر خاصی بهصورت زیر را میپذیرد:
$$E_{photon} = nhnu$$
پلانک این تابش را یک «تابش کوانتیده» (Quantized Emission) نامید. در نتیجه انرژی هر نوع تابش الکترومغناطیسی یا انرژی هر فوتون، باید بهصورت مضربی از hυ باشد.
مشکلات مدل بور
علیرغم تمام مفاهیمی که به کمک مدل بور قابل درک شده بودند، مشکل بزرگ مدل بور این بود که برای سیستمهای دارای بیشتر از یک الکترون کار نمیکرد. برای مثال مدل بور برای +He چون دارای یک الکترون است، قابل کاربرد است. یک مساله دیگری که مدل بور نمیتوانست توضیح دهد، این بود که بعدها با مشاهده دقیقتر طیف اتمی بهه شکل خطور مجزا، متوجه شدند هر خط خودش مجموعهای از خطوط کوچکتری است و این چیزی بود که در مدل بور به آن اشارهای نشد.
با اینکه بهنظر میرسید ترکیب مدل اتمی بور و رادرفورد خیلی از خواص ماده را می توانست توضیح دهد و به سرعت نیز به مدل پذیرفته شده برای اتم تبدیل شده است، اما واقعیت این بود که این ترکیب، آن مدل واقعی و درست نبود. در ادامه خواهیم دید که با پیشرفت مکانیک کوانتومی، اصلی وجود دارد که بیان میکند نمیتوانیم با قطعیت کامل مکان و انرژی الکترون در اتم را همزمان تعیین کنیم. این در حالی است که مدل بور ادعا دارد میتوان مکان و انرژی الکترون در اتم را با دقت کامل اندازهگیری کرد.
مدل کوانتومی اتم (مدل اتمی شرودینگر)
حالا که با خاصیت موجگونه الکترون آشنا شدیم، بهتر میتوانیم به مشکل بزرگ مدل بور اشاره کنیم. در این مدل، با الکترون مانند ذرهای که دقیقا در مدارهای تعریفشدهای قرار میگیرد، رفتار میشد. در سال ۱۹۲۶، دانشمند اتریشی به نام شرودینگر بر اساس نظریه دوبروی، از خاصیت موجگونه الکترونها درون اتم استفاده کرد. او در محاسبات خود به الکترون یک تابع موج نسبت داد. به این ترتیب شرودینگر مدل کوانتومی اتم را پایهگذاری کرد.

در واقع مکانیک کوانتومی به جای اینکه الکترونها را ذراتی در نظر بگیرد که دارای مکان و سرعت مشخصی هستند، آنها را موجهایی در نظر میگیرد که در محدودهای از مکانهای مجاز گسترده شدهاند. پس الکترونها دیگر در مدارهایی دور هسته نمیچرخند، اما همچنان در سطوح انرژی مشخصی به شکل ابر الکترونی قرار دارند.
در مدل کوانتومی شرودینگر، از «امواج ایستاده» (Standing Waves) بهعنوان امواج مادی الکترون استفاده شد. این امواج دارای مقادیر انرژی مجاز و مشخصی هستند. اگر بخواهیم با مثال سادهای امواج ایستاده را توضیح دهیم، زمانی که یکی از سیمهای گیتاری را جدا میکنیم، سیم به شکلی نوسان میکند که یک موج ایستاده نوسان دارد.
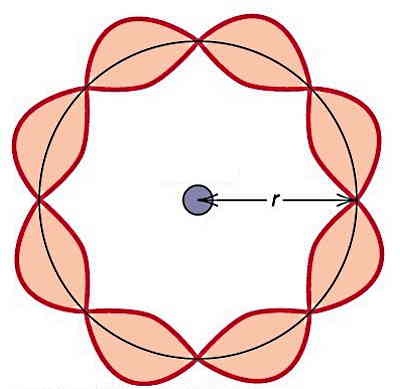
چگونه مدل کوانتومی اتم را بهتر یاد بگیریم؟

اگر میخواهید با سوالات مطرح شده در آزمونهای مختلف دوره دبیرستان در مورد مبحث مدل کوانتومی اتم آشنا شوید، نتایج این مدل را در نحوه شکلگیری مولکولها و پیوندهای شیمیایی بررسی کنید یا در سطوح بالاتر مکانیک کوانتومی، این مبحث را یاد بگیرید، استفاده از فیلمهای آموزشی فرادرس با ترتیب زیر به شما پیشنهاد میشود:
نمایش مدل کوانتومی اتم
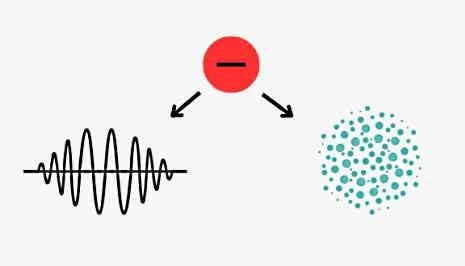
اساس نمایش مدلهای قبلی بر ذرهای بودن الکترون بود، یعنی الکترون مکان و مسیر حرکتی مشخصی داشت. اما حالا که متوجه شدیم مدل کوانتومی اتم چیست، میتوانیم نتیجهگیری کنیم که نمایش کلاسیکی اتم درست نیست. در آن ساختار، الکترون مانند سیارهای که دور خورشید میچرخد، در حال چرخش دور هسته است.

اما در مدل کوانتومی حرکت الکترونها پیشبینی میشود، بدین معنا که ما هرگز نمیتوانیم مکان دقیق الکترون در داخل اتم را تعیین کنیم. فقط میدانیم الکترونها در اطراف هسته به صورت ابری از احتمالات قرار دارند. پس در این مدل، مدار حرکت الکترون با ابری از الکترون جایگزین شده است. در واقع بهترین نمایش برای نشان دادن خاصیت موجی الکترون و امکان محاسبه احتمال حضور الکترون در سه بعد، همین مدل ابر الکترونی است. در این مدل نواحی که احتمال حضور الکترون در آنها بیشتر است، مثل نواحی نزدیکتر به هسته که ابتدا پر میشوند، پررنگتر یا چگالتر نشان داده میشوند.
پیشرفت مکانیک کوانتومی با دوگانگی موج-ذره
گفتیم که ایده اولیه شکلگیری مدل کوانتومی اتم، کشف ماهیت دوگانه موج-ذره برای الکترون بود. در این بخش میخواهیم با این مفهوم بیشتر آشنا شویم. این قدم بزرگ در پیشرفت مکانیک کوانتومی، توسط دانشمندی به نام «لویی دوبروی» (Louis de Broglie) انجام گرفت. او بر اساس کارهای پلانک و انیشتین راجعبه «دوگانگی موج-ذره» (Wave-Particle Duality) و خواص ذرهگونه امواج نوری، این فرضیه را مطرح کرد که احتمالا ذرات نیز میتوانند خواص موجگونه از خود نشان دهند. او رابطه زیر را برای طولموج ذره ای با جرم m که با سرعت v در حال حرکت است، پیشنهاد کرد:
$$lambda=frac{h}{mv}$$
در این رابطه λ طولموج دوبروی ماده بر حسب متر و h ثابت پلانک با مقدار ۶٫۶۲۶×۱۰-۳۴ J.s است.

اگر دقت کنید بین جرم و طولموج دوبروی ماده، رابطه معکوسی برقرار است. این رابطه معکوس باعث میشود تا در زندگی روزمره اثرات موجگونه مواد اطراف خود را متوجه نشویم. برای مثال زمانی که ذرهای جرمی از مرتبه حدودا ۱۰-۳۱ kg در حد و اندازه جرم الکترون داشته باشد، خواص موجگونه آن مشهود است.
طولموج دوبروی الکترون
میخواهیم بدانیم با توجه به اینکه سرعت یک الکترون در حالت پایهاش در اتم هیدروژن برابر با ۲٫۲×۱۰۶ m/s است، طولموج دوبروی آن چقدر است. میدانیم جرم الکترون ۹٫۱×۱۰-۳۱ kgاست:
$$lambda=frac{h}{mv}Rightarrowlambda=frac{6.626times10^{-34}}{(9.1times10^{-31})(2.21times10^{6})}=3.3times10^{-10} m$$
پس طولموج دوبروی الکترون از مرتبه اندازه قطر اتم هیدروژن (۱×۱۰-۱۰ m∼) است. بنابراین میتوانیم از این محاسبه اینطور نتیجهگیری کنیم که الکترون در اتم هیدروژن میتواند رفتاری موجگونه داشته باشد.
اصل عدم قطعیت هایزنبرگ
«اصل عدم قطعیت هایزنبرگ» (Heisenberg Uncertainty Principle) بیان میکند که ما نمیتوانیم همزمان در مورد مکان و انرژی یک الکترون قطعیت صد در صدی داشته باشیم. در واقع هر چه بیشتر در مورد مکان الکترون بدانیم، همزمان اطلاعاتمان در مورد انرژی الکترون کمتر خواهد بود. از آنجایی که دانستن دقیق انرژی الکترون به منظور پیشبینی واکنشهای شیمیایی اتمها مهمتر است، دانشمندان معمولا قطعیت در مورد انرژی را میپذیرند. بنابراین با دانستن دقیق انرژی، طبق اصل عدم قطعیت میتوانیم مکان الکترون را فقط بهصورت تقریبی بدانیم.
پس از توضیح اصل عدم قطعیت، حالا میتوانیم بگوییم مدل کوانتومی اتم بر پایه دو ستون استوار شامل رفتار دوگانه الکترون و اصل عدم قطعیت شکل گرفته است. حال چطور میتوانیم بهصورت تقریبی مکان الکترون درون اتم را محاسبه کنیم؟ میتوانیم از توابعموجی که از حل معادله شرودینگر برای یک اتم خاص بدست میآیند، استفاده کنیم. به این ترتیب، احتمال پیدا کردن یک الکترون در ناحیه خاصی درون اتم با محاسبه $${midpsimid}^2$$ بدست میآید.
معادله موج شرودینگر
شرودینگر یکی از سختترین معادلات جهان را حل کرد تا توصیف دقیقتری از رفتار الکترونها در اتم هیدروژن ارائه کند. او برای این کار مهمی که انجام داد موفق به دریافت جایزه نوبل نیز شد. شرودینگر وضعیت الکترون در اتم را مانند یک موج در نظر گرفت و بر این اساس سعی کرد احتمال حضور الکترون در هر نقطه درون اتم را محاسبه کند. معادله دیفرانسیلی معروفی که میتواند این احتمال را محاسبه کند، معادله موج شرودینگر است:
$$hat{H}psi = E psi$$
در این رابطه H عملگر یا اپراتور هامیلتونی، E ویژه مقدار انرژی الکترون و Ψ تابعموج الکترون است. پس از حل این معادله، مجموعهای از ψها را خواهیم داشت که برای هر کدام، یک انرژی E وجود دارد. در این مدل هم مانند مدل اتم بور، مقادیر انرژی کوانتیده هستند. اما در اینجا کوانتیزیشن از ماهیت موجی الکترون ناشی شده است و پاسخهای کوانتیده از حل معادله موج شرودینگر بدست میآیند.
اوربیتالهای اتمی
تا اینجا یاد گرفتیم که مدل کوانتومی اتم بر مبنای احتمال یافتن الکترون در یک ناحیه کار میکند. اگر بخواهیم احتمال حضور الکترون در یک ناحیه را با یک شکل نشان دهیم، این شکل میتواند همان «اوربیتال اتمی» (Atomic Orbital) باشد. در واقع ناحیهای که الکترون %90 از زمان خود را در آن سپری کند، اوربیتال اتمی نام دارد.
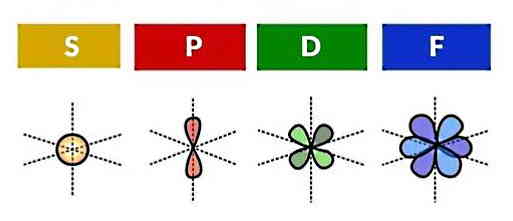
از بخش مدل بور به یاد داریم که توزیع الکترونها در لایهها به چه صورت انجام میشد. هر لایه دارای زیرلایهها یا زیرپوستههایی (Subshells) است که آنها نیز متشکل از اوربیتالهای اتمی هستند. بنابراین با شناخت اوربیتالهای اتمی میتوانیم بهصورت دقیقتری نحوه قرار گرفتن الکترونها درون اتم را یاد بگیریم.
شکل اوربیتالهای اتمی علاوه بر فاصله الکترون از هسته، به موقعیت زاویهای الکترون نسبت به هسته نیز وابسته است. همین مساله موجب شده تا شکلهای مختلفی برای اوربیتالهای اتمی داشته باشیم. کمیت ریاضیاتی که اوربیتالها را بهخوبی توصیف میکند، تابع موج است. در شکل زیر، نواحی پررنگ و کمرنگ نشان دهنده علامت تابع موج الکترون هستند (علامت منفی یا مثبت). زمانی که تابع موج تغییر علامت میدهد، در نمایش مکان الکترون در اوربیتال یک «گره» (Node) داریم. پس گرهها نشاندهنده احتمال صفر برای حضور الکترون هستند.
هر اوربیتال میتواند حداکثر توسط دو الکترون اشغال شود. اگر به نمایش مدل کوانتومی که در بخشهای قبل به آن اشاره شد دقت کنیم، ابر الکترونی برآیندی از تمام اوربیتالهای اتمی است. رسم شکل دقیق اوربیتالهای اتمی در سه بعد، کار سادهای نیست و به همین دلیل از نمایش ابر الکترونی استفاده میشود. در ادامه اوربیتالهای اتمی را همراه با ویژگیهایشان توضیح میدهیم.
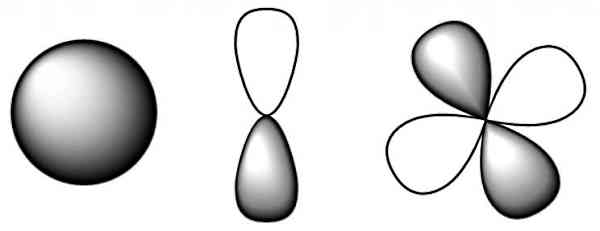
اوربیتال کروی s
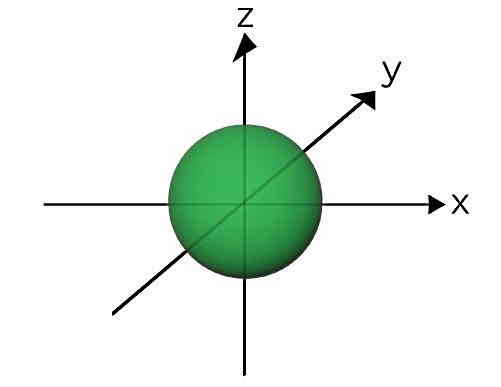
تک اوربیتال s دارای تقارن کروی نسبت به سه محور مختصات xyz است. بنابراین شکل آن کروی است. تابع موج الکترون در این ناحیه فقط به فاصله الکترون از هسته بستگی دارد. در این اوربیتال حداکثر دو الکترون میتوانند قرار بگیرند. یک نکته مهم در مورد اوربیتالهای اتمی، نحوه پر شدن آنها است که از قاعده خاصی پیروی میکند. در مورد اوربیتال s، همیشه پر شدن الکترونها در اتم از این ناحیه شروع می شود. در اوربیتال s هیچ گرهای نداریم.
اوربیتالهای p
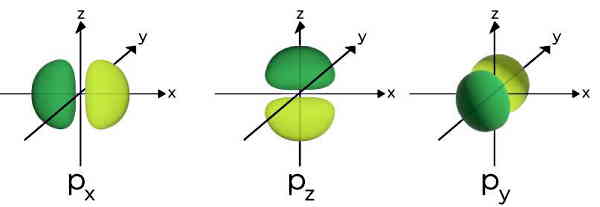
سه اوربیتال p شبیه بادام زمینی یا دمبلیشکل هستند. با توجه به اینکه هر اوربیتال p میتواند در یک راستای مختصات جهتگیری داشته باشد، بنابراین دارای سه جهتگیری با نامهای p۰، p-۱ و p۱ هستند. در هر کدام از اوربیتالهای p، حداکثر دو الکترون قرار میگیرند. پس در مجموع میتوانیم شش الکترون را در سه اوربیتال p قرار دهیم. همچنین در هر اوربیتال p یک گره داریم.
اوربیتالهای d
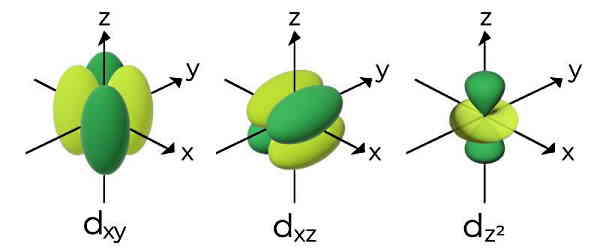
پنج اوربیتال d حداکثر ده الکترون را میتوانند در خود جای دهند. شکل هر اوربیتال d بهصورت دو دمبل متقاطع یا شبدر چهار برگ است. چهار عدد از این اوربیتالها میتوانند چهار جهتگیری مختلف داشته باشند و یکی از آنها شکلی شبیه به اوربیتال p خواهد داشت. در هر اوربیتال d دو گره داریم.
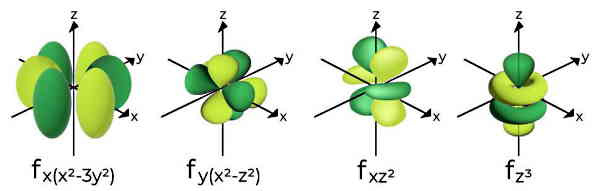
اوربیتالهای f
هفت اوربیتال f با جای دادن حداکثر چهارده الکترون دارای شکل پیچیدهتری نسبت به بقیه اوربیتالها هستند.
اسپین الکترون
الکترون دارای یک خاصیت ذاتی به نام «اسپین» (Spin) است که همواره در یکی از دو حالت اسپین بالا (↑) یا اسپین پایین (↓) قرار میگیرد. برای نشان دادن این خاصیت از کمیتی به نام «عدد کوانتومی اسپینی» (Spin Quantum Number) که با ms نشان داده میشود، استفاده میکنند. مقدار این عدد کوانتومی مشخص میکند که الکترون در چه جهتی در حال چرخش است.
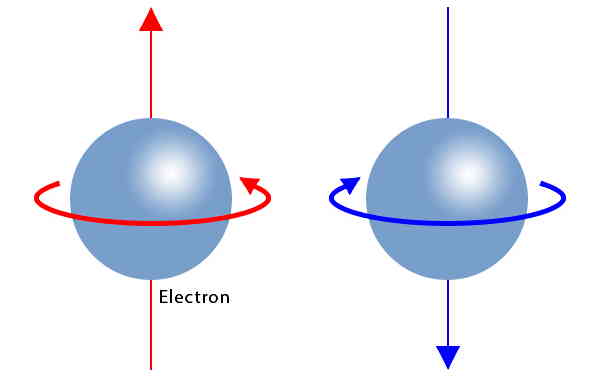
دو مقدار مجاز برای این عدد +۱/۲ برای اسپین بالا یا چرخش ساعتگرد و -۱/۲ برای اسپین پایین یا چرخش پادساعتگرد است. همچنین طبق «اصل طرد پاولی» (Pauli Exclusion Principle) ثابت شده است که هر دو الکترون حاضر در یک اوربیتال اتمی، حتما اسپینهایی در خلاف جهت هم دارند. از این عدد کوانتومی جهت تعیین توانایی تولید میدان مغناطیسی توسط اتم مورد بررسی استفاده میشود.
اعداد کوانتومی
پس از آشنایی با مفهوم اوربیتالهای اتمی و اسپین، حالا میتوانیم یک قدم جلوتر برویم و هر الکترون را با استفاده از چهار عدد کوانتومی از الکترون دیگر متمایز کنیم. در بخش مدل اتم هیدروژن بور، با عدد کوانتومی اصلی n و در بخش اسپین الکترون با عدد کوانتومی اسپینی ms آشنا شدیم. مهم است بدانیم مقدار عدد کوانتومی اسپینی مستقل از مقادیر سایر اعداد کوانتومی است.
اعداد کوانتومی نشاندهنده موقعیت و در نتیجه انرژی هر الکترون در اتم هستند. کاربرد مهم دیگر این اعداد، در حل آسانتر معادله موج شرودینگر است. چهار عدد کوانتومی بهصورت زیر هستند:
- عدد کوانتومی اصلی (Principal Quantum Number) یا n
- عدد کوانتومی فرعی یا عدد کوانتومی اندازه حرکت زاویهای مداری (Azimuthal Quantum Number) یا l
- عدد کوانتومی مغناطیسی (Magnetic Quantum Number) یا ml
- عدد کوانتومی اسپینی (Spin Quantum Number) یا ms
| مقادیر مجاز | عدد کوانتومی |
| $$1, 2, 3, 4, …$$ | عدد کوانتومی اصلی n (نشاندهنده لایهها) |
| $$0, 1, 2, 3, 4, …, (n-1)$$ | عدد کوانتومی فرعی l (نشاندهنده زیرلایهها) |
| $$-l, …, -1, 0, 1, …, l$$ | عدد کوانتومی مغناطیسی $$m_l$$ (نشاندهنده جهتگیری و تعداد کل اوربیتالها) |
| $$+1/2, -1/2$$ | عدد کوانتومی اسپینی $$m_s$$ (نشاندهنده جهت چرخش الکترون) |
عدد کوانتومی فرعی
همانطور که در جدول بخش قبل می توانید ببینید، مقدار l یا عدد کوانتومی فرعی به مقدار n بستگی دارد و همیشه یک واحد از آن کمتر است. در واقع به ازای هر مقدار n، همواره l مقدار صحیحی از ۰ تا n-۱ دارد. مقدار l تعیینکننده نوع اوربیتال اتمی یا شکل سه بعدی زیرلایهها است، به این صورت که برای l=۰ اوربیتال s، برای l=۱ اوربیتال p، برای l=۲ اوربیتال d، برای l=۳ اوربیتال f و … داریم. مثلا اگر n=۳ باشد، مقادیر ممکن برای l شامل ۰، ۱ و ۲ است. بنابراین اوبیتالهای s و p و d را خواهیم داشت که بهصورت دقیقتر به شکل زیر نشان داده میشوند:
- n=۳ و l=۰: اوربیتال ۳s
- n=۳ و l=۱: اوربیتال ۳p
- n=۳ و l=۲: اوربیتال ۳d
یا بهطور مثال اوربیتالی به نام ۲d نداریم. چون برای n=۲ مقادیر مجاز l شامل ۰ و ۱ هستند که شامل اوربیتالهای اتمی s و p میشوند. اوربیتال d معادل l=۳ است که مقدار مجاز l برای این n نیست.
نکته مهم دیگر این است که مقدار عدد کوانتومی مغناطیسی نیز به مقدار عدد کوانتومی فرعی l و در نتیجه بهصورت غیر مستقیم به n بستگی دارد. برای مثال در مورد n=۳ برای مقادیر مجاز ml خواهیم داشت: $$-2, -1 , 0, +1, +2$$. همچنین مقدار l میتواند تعداد کل اوربیتالهایی که الکترونها در اتم پر میکنند، را طبق رابطه ۲l+۱ به ما بدهد.
| مقادیر مجاز برای $$m_l$$ | تعداد اوربیتالهای متناظر (2l+1) | عدد کوانتومی فرعی l |
| 0 | $$2times0+1=1$$ | 0 (زیرلایه s) |
| $$-1, 0, 1$$ | $$2times1+1=3$$ | 1 (زیرلایه p) |
| $$-2, -1, 0, 1, 2$$ | $$2times2+1=5$$ | 2 (زیرلایه d) |
| $$-3, -2, -1, 0, 1, 2, 3$$ | $$2times3+1=7$$ | 3 (زیرلایه f) |
تمام نکات مطرح شده بهطور خلاصه در جدول بالا آورده شدهاند. در نهایت طبق «قواعد هوند» (Hund’s Rules) امکان ندارد که دو الکترون از یک اتم دارای مقادیر کاملا یکسانی از اعداد کوانتومی باشند. در بهترین حالت، حتی برای دو الکترون که در یک حالت انرژی قرار دارند، اسپینها در جهت مخالف هم هستند. با بررسی چند مثال بهتر میتوانیم متوجه قواعد بیان شده بشویم.
مثال ۱
برای لایه n=۴ در یک اتم، تعداد زیرلایهها، اوربیتالهای هر زیرلایه و مقادیر l و ml اوربیتالها را پیدا کنید:
پاسخ
برای n=۴ مقدار l به صورت ۰، ۱، ۲، و ۳ است. بنابراین زیرلایههایی به شکل اوربیتالهای s و p و f در لایه n=۴ اتم دیده میشوند.
- برای l=۰ (زیرلایه s) ml فقط میتواند مقدار صفر را داشته باشد. بنابراین فقط اوربیتال ۴s را داریم.
- برای l=۱ (اوربیتالهای نوع p) ml میتواند مقادیر ۱+ و ۰ و ۱- را داشته باشد. بنابراین سه اوربیتال ۴p را داریم.
- برای l=۲ (اوربیتالهای نوع d) ml میتواند مقادیر ۲+ و ۱+ و ۰ و ۱- و ۲- را داشته باشد. بنابراین پنج اوربیتال ۴d را داریم.
- برای l=۳ (اوربیتالهای نوع f) ml میتواند مقادیر ۳+ و ۲+ و ۱+ و ۰ و ۱- و ۲- و ۳ـ را داشته باشد. بنابراین هفت اوربیتال ۴f را داریم.
بنابراین در مجموع ۱۶ اوربیتال در لایه n=۴ این اتم پیدا کردیم.
مثال ۲
بیشترین تعداد الکترونهایی که میتوانند لایه n=۴ را پر کنند، محاسبه کنید.
پاسخ
در این حالت، چهار زیرلایه داریم که با هم جمع میشوند:
- یک اوربیتال ۴s
- سه اوربیتال ۴p
- پنج اوربیتال ۴d
- هفت اوربیتال ۴f
دقت داریم که هر اوربیتال دو الکترون در خود جای میدهد. بنابراین در ۱۶ اوربیتال ۳۲ الکترون خواهیم داشت.
جذب و گسیل فوتون
در این بخش میخواهیم با توجه به در نظر گرفتن مدل بور برای اتم، برای سطح انرژی الکترون «حالت پایه» (Ground State) و «حالت برانگیخته» (Excited State) را معرفی کنیم. این دو حالت مهم منشا فرآیندهای «جذب» (Absorption) و «گسیل، نشر یا تابش» (Emission) فوتون در عناصر مختلف هستند. مدل اتم هیدروژن بور بهخوبی میتواند فرآیندهای جذب و گسیل فوتون را توضیح دهد.
حالت پایه چیست؟
کمترین مقدار انرژیای که الکترون در ساختار یک اتم میتواند داشته باشد، حالت پایه است. اگر به رابطه انرژی در مدل اتم هیدروژن بور دقت کنیم، مقدار این انرژی با قرار دادن n=۱ بدست میآید و برابر است با E(۱)=-۱۳٫۶ eV. پس باید دقت کنیم که گستره عددی انرژی در بازه ۱۳٫۶- تا 0 قرار دارد. یعنی انرژی از n=۱ با کمترین مقدار E(1)=-۱۳٫۶ eV شروع میشود و با افزایش n، مقدار انرژی بیشتر خواهد شد. در نهایت انرژی به صفر میرسد، که در این حالت الکترون کاملا از اتم جدا شده است.
حالت برانگیخته چیست؟
طبق مدل اتم هیدروژن بور، یک الکترون میتواند با جذب انرژی در قالب فوتون به سطح انرژی بالاتری برود. البته لازم است مقدار انرژی این فوتون، با اختلاف انرژی اولیه و نهایی الکترون برابر باشد. وقتی الکترون به سطحی با انرژی بالاتر رفت، میگوییم الکترون در حالت برانگیخته است. در حالت برانگیخته، الکترون نسبت به قبل پایداری کمتری دارد و ممکن است با گسیل یک فوتون به حالت پایدار پایینتر بازگردد. بازگشت الکترون به حالتی با انرژی پایینتر که همراه با گسیل فوتون است را «ریلکسیشن» (Relaxation) میگویند.
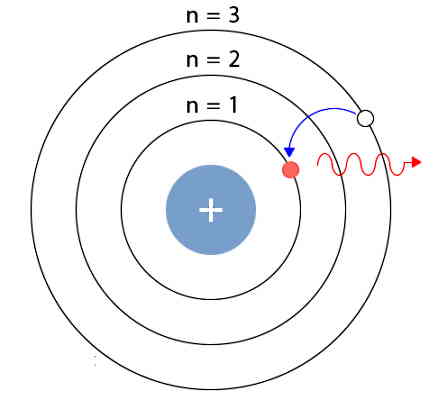
اگر بخواهیم تفاوت انرژی برای یک انتقال فرضی الکترون را محاسبه کنیم، داریم:
$$triangle E =E(n_{high})-E(n_{low})=(frac{-13.6 eV}{n^2_{high}})-(frac{-13.6 eV}{n^2_{low}})= (frac{1}{{n^2_{low}}} -frac{1}{{n^2_{high}}}). 13.6 eV $$
در این رابطه nhigh عدد کوانتومی مربوط به مدار بالاتر یا حالتی با انرژی بیشتر و nlow عدد کوانتومی مربوط به مدار پایینتر یا حالتی با انرژی پایینتر است. چون رابطه بین انرژی یک فوتون و فرکانس آن را از فرمول پلانک میدانیم، بنابراین میتوانیم فرکانس فوتون گسیل شده را نیز محاسبه کنیم:
$$nu =frac{13.6 eV}{h} (frac{1}{{n^2_{low}}} -frac{1}{{n^2_{high}}}) $$
به همین ترتیب، با استفاده از رابطه υλ=c میتوانیم طولموج این فوتون را نیز محاسبه کنیم.
طیف اتمی
گفتیم که در اتم فرآیندهای جذب و گسیل فوتون اتفاق میافتد. گسیل یا نشر فوتون توسط اتمهای یک ماده باعث ایجاد خطوطی با رنگهای مختلف خواهد شد که توسط یک آشکارساز قابل مشاهدهاند. مجموعه این خطوط در کنار هم را «طیف نشری اتمی» (Atomic Emission Spectra) یا «طیف خطی» (Line Spectrum) مینامند. خطوط با رنگهای مختلف، نشاندهنده گسیل طولموجهای مختلف است. این طیف برای هر عنصر با عنصر دیگر متفاوت است و به نوعی مشخصهای برای تشخیص عناصر محسوب میشود.
بور توانست با مطالعه فوتونهایی که توسط الکترون جذب یا گسیل میشوند، طیف اتم هیدروژن را توضیح دهد. شکل زیر ناحیه مرئی طیف تابشی اتم هیدروژن را نشان میدهد. همانطور که در شکل مشخص است، هیدروژن تقریبا چهار طولموج ناحیه مرئی را گسیل میکند. برای اتم سادهای مانند اتم هیدروژن میتوان طولموجهای برخی از خطوط تابش را در قالب روابط ریاضیاتی نیز بیان کرد.

در بخش قبل گفتیم که میتوانیم طولموج فوتونهای گسیل شده را محاسبه کنیم. اگر از رابطه بور استفاده کنیم، برای طولموج طیف هیدروژن رابطه زیر را خواهیم داشت که به «فرمول ریدبرگ» (Rydberg Formula) مشهور است:
$$frac{1}{lambda} =R_H (frac{1}{{n^2_{low}}} -frac{1}{{n^2_{high}}}) $$
- RH ثابت ریدبرگ برای اتم هیدروژن است و مقدار آن ۱۰۹۶۷۷ cm-1 است.
- λ طولموج فوتون گسیل شده در خلا بر حسب cm است.
- n عدد صحیح است و همواره داریم: nlow < nhigh
همچنین به یاد داریم که طبق مدل بور، هر الکترون میتواند با جذب انرژی در قالب فوتون به حالتهایی با انرژی بالاتر برود یا برانگیخته شود. همچنین الکترون برانگیخته که در حالتی با پایداری کمتر نسبت به قبل قرار دارد، میتواند با گسیل فوتون به حالت پایین پایدارتر بازگردد. سطوح انرژی و انتقالهای (Transitions) بین آنها را میتوانیم با «دیاگرام سطح انرژی» (Energy Level Diagram) نمایش دهیم. شکل زیر دیاگرام سطح انرژی اتم هیدروژن را نشان میدهد.
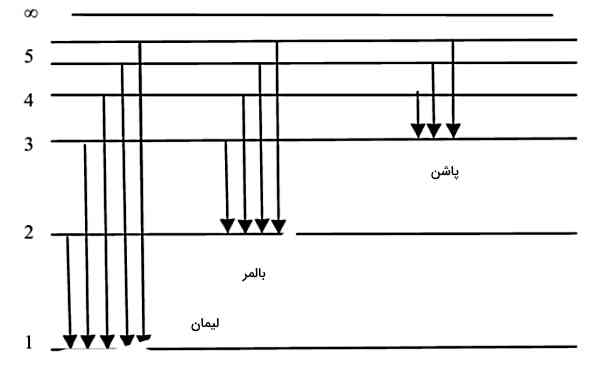
فرآیندهای جذب و گسیل فوتون در اتم هیدروژن، باعث تشکیل سریهایی به نام «سری لیمان» (Lyman Series)، «سری بالمر» (Balmer Series) و «سری پاشن» (Paschen Series) میشوند که در ادامه به توضیح تفاوت این سریها خواهیم پرداخت.
سری لیمان
تفاوت سریهای مختلف طیف نشری اتم هیدروژن در پایینترین سطح انرژیای است که در انتقالهای آن سری دخیل است. در سری لیمان انتقالهایی داریم که شروع یا انتهای آنها از حالت پایه اتم هیدروژن یا سطح انرژی n=۱ است. گاز شفاف هیدروژن را در نظر بگیرید. اگر این گاز تا دمای کمتر از ۱۰۰۰۰ کلوین سرد شود، بیشتر الکترونهای اتمهای این گاز در حالت پایه قرار میگیرند. حالا اگر از این گاز نوری عبور دهیم، جذب سری لیمان اتفاق خواهد افتاد.
اگر در فرمول ریدبرگ nlow=۱ را قرار دهیم و nhigh=۲ تا ∞=nhigh را در نظر بگیریم، خطوط طیفی به سمت طولموج حدودی ۹۱ nm همگرا خواهند شد که معادل محدوده فرابنفش است. بنابراین سری لیمان، در ناحیه فرابنفش طیف نشری اتم هیدروژن است.
سری بالمر
حالا گاز هیدروژن شفاف ولی گرمتر با دمایی حدود ۱۰۰۰۰ کلوین را در نظر بگیرید، طوری که تمام الکترونهای آن در اولین حالت برانگیخته باشند. با عبور نور از این گاز، جذب سری بالمر را خواهیم داشت. در سری بالمر انتقالهایی داریم که شروع یا انتهای آنها در اولین حالت برانگیخته اتم هیدروژن یا سطح انرژی n=۲ است.
شکل زیر دیاگرام سطح انرژی سری بالمر برای الکترونهای اتم هیدروژن را نشان میدهد که با بازگشت به سطح انرژی n=۲ ریلکس میشوند.
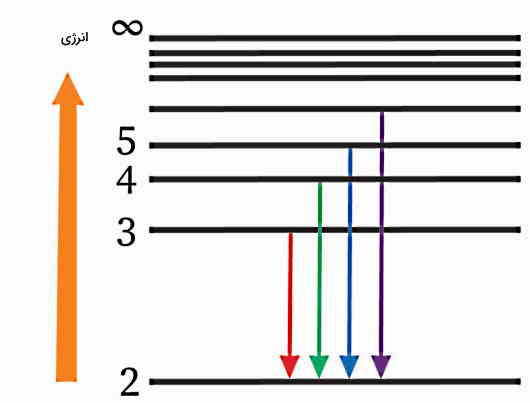
اگر دقت کنیم این شکل مطابق است با فرایند ریلکسیشن الکترونهای اتم هیدروژن از سطوح n=۳ تا n=۵ به سطح n=۲. در واقع، با استفاده از فرمول ریدبرگ و قراردهی nlow=۲ و nhigh=۳ تا ∞=nhigh، خطوط طیفی به سمت ۳۶۵ nm همگرا خواهند شد که محدوده طیف مرئی است. پس سری بالمر خطوط طیفی در ناحیه مرئی طیف نشری اتم هیدروژن است.
سری پاشن
با گرم کردن گاز هیدروژن تا دمای حدودا ۲۵۰۰۰ کلوین، بیشتر الکترونهای آن در دومین حالت برانگیخته قرار میگیرند. سری پاشن شامل انتقالهایی است که از سطح انرژی n=۳ شروع یا به این سطح ختم میشوند. سری پاشن، در ناحیه ماورای قرمز طیف نشری اتم هیدروژن است. اگر در فرمول ریدبرگ nlow=۳ و nhigh=۴ تا ∞=nhigh را در نظر بگیریم، همگرایی خطوط طیفی به سمت ۸۲۱ nm است.
توزیع الکترون در لایهها (عدد کوانتومی اصلی)
حالا میخواهیم ببینیم نحوه قرارگیری الکترونها در مدارهای مجاز یا همان لایههای مجاز چگونه است. دیدیم که فرمولبندی بور برای شعاع و انرژیهای مجاز بر پایه عددی به نام n انجام شد. n را «عدد کوانتومی اصلی» (Principal Quantum Number) مینامیم و خواهیم دید در مدل کوانتومی نیز از این عدد استفاده میشود. چون این لایهها همان مقادیر مجاز برای n هستند، پس میتوانیم این لایهها را سطوح انرژی هم بنامیم:
- n=۱: لایه K
- n=۲: لایه L
- n=۳: لایه M
- n=۴: لایه N
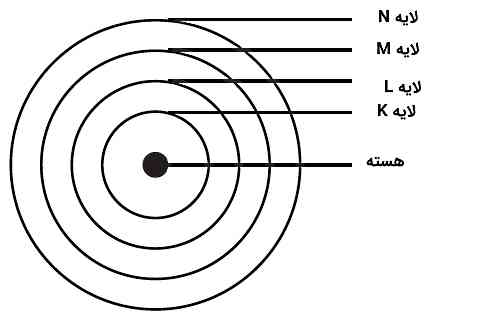
به یاد داریم که همیشه مقدار n یک عدد صحیح و مثبت (مخالف صفر) است، یعنی برای n داریم همیشه n≥۱. بیشترین تعداد الکترونهایی که میتوانند در یک لایه قرار بگیرند، از رابطه ۲n۲ محاسبه میشود. طبق این رابطه، در n=۱ که لایه K و درونیترین لایه هم محسوب میشود، حداکثر دو الکترون میتواند قرار بگیرد. ترتیب قرارگیری الکترونها در اتم نیز از همین لایه شروع میشود و پس از پر شدن آن، الکترونها وارد لایههای بعدی با n بزرگتر خواهند شد. پس هر چه مقدار n بیشتر باشد، الکترون در فاصله دورتری از هسته با سطح انرژی بالاتری قرار دارد.
زمانی که الکترونی از حالت پایه به حالت برانگیخته میرود، در واقع مقدار عدد n برای این الکترون افزایش خواهد یافت. معمولا افزایش n برای یک الکترون، همانطور که قبلا گفتیم با دریافت فوتون یا گرما اتفاق میافتد. اما اگر الکترونی از حالت برانگیخته به حالت پایه برود، n کاهش یافته و در این حالت گسیل فوتون داریم. بنابراین با افزایش n جذب و با کاهش n گسیل خواهیم داشت.
توزیع الکترون در زیرلایهها
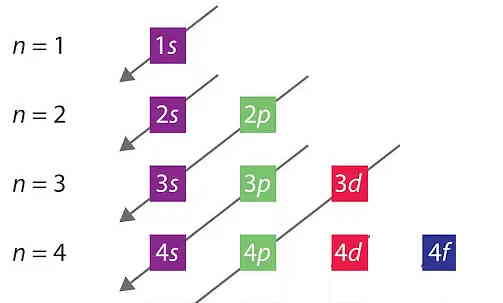
با یادگیری مفهوم لایه، زیرلایه و اوربیتال اتمی میتوانیم دقیقتر بررسی کنیم که الکترونها به چه صورت اتم را پر میکنند. چیزی که در ترتیب پر شدن زیرلایهها مهم است، سطح انرژی آنها است. یعنی ابتدا زیرلایههای دارای انرژی کمتر پر میشوند و سپس زیرلایههای دارای انرژی بالاتر. این روند «اصل آفبا» (Aufbau Principle) نام دارد. طبق این اصل، زیرلایههای دارای مقدار n+۱ کمتر، ابتدا پر میشوند.
| نحوه توزیع الکترونها در زیرلایه | بیشترین تعداد الکترونهای لایه | نام زیرلایه | نام لایه |
| $$1s^2$$ | 2 | 1s | K |
| $$2s^2 2p^6$$ | 8 | 2s, 2p | L |
| $$3s^2 3p^6 3d^{10}$$ | 18 | 3s, 3p, 3d | M |
| $$4s^2 4p^6 4d^10 4f^{14}$$ | 32 | 4s, 4p, 4d, 4f | N |
مثلا سطح انرژی ۴s و ۳d را اگر مقایسه کنیم، برای ۴s مقدار n+۱ برابر است با ۴ در حالی که برای ۳d این مقدار ۵ است. پس ابتدا ۴s پر میشود و اگر همچنان الکترونی باقی مانده بود، این الکترونها ۳d را پر میکنند. روند کلی نحوه پر شدن زیرلایهها توسط الکترونها بر اساس اصل آفبا در شکل زیر نشان داده شده است.
کاربرد مدل کوانتومی اتم
یکی از کاربردهای مدل کوانتومی اتم یا مدل ابری الکترون، توضیح دقیقتر چگونگی پیوند دو اتم است. وقتی که دو اتم به هم نزدیک میشوند تا یک مولکول را شکل دهند، ابر الکترونی دو اتم «اورلپ یا همپوشانی» (Overlap) خواهند داشت. به این ترتیب ناحیهای در فضا تشکیل میدهند که در آنجا احتمال یافتن الکترون خیلی بیشتر از احتمال یافتن الکترون در ابر الکترونی هر یک از دو اتم بهطور مجزا است.
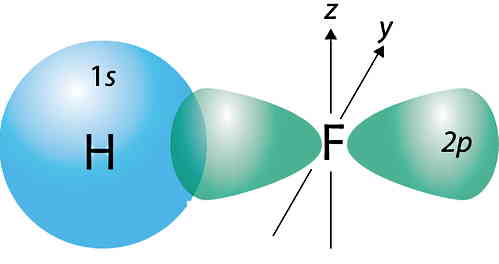
این همپوشانی ابر الکترونی اتمها، تعیینکننده خواص و شکل مولکولها است. برای مثال، در شکل بالا همپوشانی دو ابر الکترونی برای اوربیتالهای s و p باعث ایجاد پیوند و تشکیل مولکول هیدروژن فلورید (HF) شده است.
سایر مدلهای اتمی
ساختار اتمی نشاندهنده اجزای یک اتم و نحوه قرارگیری آنها نسبت به هم است. سادهترین ساختار اتمی شامل یک هسته در مرکز اتم است که الکترونهایی با بار منفی دور آن قرار دارند. خود هسته شامل ذراتی با بار مثبت به نام پروتون و ذراتی بدون بار یا خنثی به نام نوترون است. از آنجا که اتمهای عناصر مختلف دارای تعداد الکترونها و پروتونهای متفاوتی هستند، در نتیجه ساختار اتمی متفاوتی خواهند داشت که این مسئله باعث ایجاد خواص متفاوت عناصر میشود.
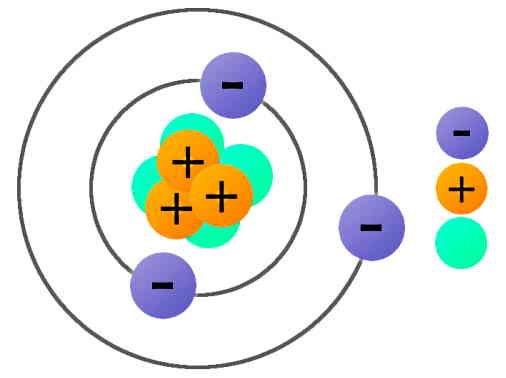
در یک اتم، تعداد الکترونها و پروتونها با هم برابر است. بنابراین اتم از نظر الکتریکی خنثی است. تعداد پروتونهای یک عنصر با «عدد اتمی» (Atomic Number) آن عنصر مشخص میشود. همچنین ممکن است طی فعل و انفعالات شیمیایی و به جهت حفظ پایداری، اتم الکترون از دست بدهد یا الکترون اضافی دریافت کند. در این حالت اتم به «یون» (Ion) تبدیل میشود. بنابراین، یک یون از لحاظ الکتریکی خنثی نیست.
«ذرات زیراتمی» (Subatomic Particles) شامل پروتونها، الکترونها و نوترونها هستند. جدول زیر خصوصیات این ذرات را بهصورت خلاصه نشان میدهد. در جدول واضح است که پروتونها از الکترونها بسیار سنگینتراند و در نتیجه بیشتر جرم اتم در هسته متمرکز است. بهخصوص که جرم نوترونها هم با جرم پروتونها تقریبا برابر است. با وجود سبک بودن الکترونها، همچنان این ذرات در شکلگیری خواص مواد بسیار تعیینکننده هستند.
| بار (کولن) | جرم (kg) | ذرات زیراتمی |
| $$1.602times10^{-19}$$ (مثبت) | $$1.672times10^{-24}$$ | پروتون |
| بدون بار | $$1.674times10^{-24}$$ | نوترون |
| $$1.602times10^{-19}$$ (منفی) | $$9.1times10^{-31}$$ | الکترون |
در قرن هجدهم و نوزدهم، دانشمندان زیادی تلاش کردند تا ساختار اتم را بر اساس مدلهایی که مطرح میکردند، توضیح دهند. مهمترین مدلهایی که برای شناسایی ساختار اتم پیشنهاد شدند، شامل موارد زیر هستند:
- تئوری اتمی دالتون
- مدل کیک کشمشی تامسون (کشف الکترون)
- مدل هستهای رادرفورد (کشف هسته)
- مدل سیارهای بور
- مدل مکانیک کوانتومی اتم
در هر مدل جدیدی که ارائه میشد، سعی بر این بود که برای سوالات و مشکلات مدلهای قبلی پاسخی ارائه شود. تمام مدلهای پیش از مدل اتمی بور، کلاسیکی محسوب میشوند. مدل بور اولین مدلی بود که بر پایه فرضیات غیرکلاسیکی مطرح شد. در ادامه در مورد ساختار اتمی پیشنهاد شده توسط هر کدام از این مدلها توضیح مختصری بیان میشود. خواهیم دید چه روندی در علم طی شد تا در نهایت به اینکه مدل کوانتومی اتم چیست، رسیدیم.
تئوری اتمی دالتون
در سال ۱۸۰۸، «جان دالتون» (John Dalton) برای اولین بار پیشنهاد کرد که ماده از ذرات ریز و نامرئی به نام اتم تشکیل شده است. او معتقد بود اتمها کوچکترین اجزای تشکیل دهنده مادهاند و قابل شکستن به ذرات ریزتر نیستند. بنابراین در نظریه دالتون، اتمها عامل انجام واکنشها محسوب میشدند.

از نظر دالتون تمام اتمهای یک عنصر کاملا یکسان بودند ولی اتمهای عناصر مختلف از نظر اندازه و جرم با هم فرق داشتند. تئوری دالتون مشکلات زیادی داشت. برای مثال این مدل نمیتوانست وجود «ایزوتوپها» (Isotopes) را توضیح دهد. همچنین بعدها مشخص شد که اتمها قابل دیدناند و ادعای دالتون اشتباه بوده است. با کشف ذرات زیراتمی مانند الکترون، نظریه دالتون تقریبا کنار گذاشته شد.

مدل کیک کشمشی تامسون (کشف الکترون)
«جوزف جان تامسون» (Joseph John Thomson) اتم را بهصورت کرهای متشکل از بارهای مثبت فرض کرد که الکترونهای با بار منفی را در داخل خود جای داده است. بنابراین از دیدگاه تامسون، اتم از نظر الکتریکی خنثی بود. او اسم مدل خود را «مدل کیک کشمشی» (Plum Pudding Model) گذاشت، چون الکترونهای داخل اتم را مانند کشمشهای داخل یک کیک در نظر گرفته بود.

کار مهمی که جی جی تامسون در سال ۱۸۹۷ انجام داد این بود که با انجام «آزمایش اشعه کاتدی» (Cathode Ray Experiment)، موفق به کشف الکترون و دریافت جایزه نوبل شد. اما مشکل مدل تامسون این بود که نمیتوانست پایداری اتم را توجیه کند. همچنین برخی ذرات زیراتمی که بعدها کشف شدند را نمیتوانست توضیح دهد.

مدل هستهای رادرفورد (کشف هسته)
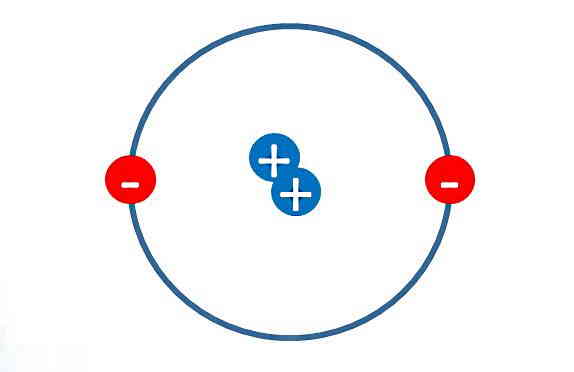
ارنست رادرفورد (Ernest Rutherford) شاگرد تامسون بود. او در سال ۱۹۱۱ با انجام «آزمایش پراکندگی اشعه آلفا» (Alpha Ray Scattering Experiment) موفق به کشف هسته شد. رادرفورد هسته را در مرکز اتم قرار دارد، طوری که الکترونها به دور هسته در حال چرخشاند. در واقع طبق مدل هستهای رادرفورد، بخش بزرگی از فضای داخل اتم خالی است و فقط یک ناحیه کوچک و چگال در مرکز اتم وجود دارد. اون این ناحیه را هسته نامید. بر این اساس بیشتر جرم اتم در هسته متمرکز است.
اما مشکل مدل رادرفورد چه بود؟ طبق این مدل الکترونها با حرکت دور هسته میتوانند شتاب بگیرند. ولی طبق تئوری الکترومغناطیس، میدانیم وقتی که یک ذره باردار حرکت شتابدار داشته باشد، انرژی از دست خواهد داد. به این ترتیب الکترونها کمکم تمام انرژی خود را از دست میدهند و اتم از هم میپاشد. بنابراین همچنان مشکل پایداری اتم در این مدل هم به جای خود باقی است.

همچنین رادرفورد در مورد اینکه الکترونها همگی در یک مدار قرار میگیرند یا در مدارهای مختلفی، توضیحی ارائه نداد. مساله مهم بعدی این بود که اگر الکترونها پیوسته در حال گردش دور هستهاند، اتم باید یک طیف پیوسته گسیل کند. اما در واقعیت چیزی که بعدها مشاهده شد، گسیل خطوطی مجزا و تفکیک شده بود.
جمعبندی
در این مطلب از مجله فرادرس ابتدا برخی مدلهای کلاسیکی اتم و مشکلاتشان توضیح داده شدند. سپس دیدیم که استفاده از دیدگاه کوانتومی برای مدل سازی ساختار اتم، میتواند مشکلات مدلهای قبل را حل کند. پس در مجموع نکات زیر را یاد گرفتیم:
- مدل بور بر پایه مفروضات نیمهکلاسیکی و ذرهای بودن الکترون ارائه شد.
- در مدل بور انرژی کوانتیده است و الکترونها در مدارهای دایرهای شکل مشخصی در حال حرکت به دور هسته هستند.
- مدل بور توانست انرژی هر الکترون در مدار nام را محاسبه کند و طیف اتم هیدروژن را نیز توضیح دهد.
- مشکل مدل بور این بود که فقط برای اتمهای دارای یک الکترون مثل اتم هیدروژن کارایی داشت.
- در مدل کوانتومی اتم، الکترون رفتار موجگونه دارد و این خاصیت با نمایش ابر الکترونی نشان داده میشود.
- احتمال یافتن الکترون در یک نقطه درون اتم را میتوان با داشتن تابع موج الکترون تعیین کرد.
- حل معادله موج شرودینگر اطلاعات مهمی در مورد وضعیت قرارگیری الکترون در لایهها و اوربیتالهای اتمی بدست میدهد.
- در مدل کوانتومی اتم با استفاده از چهار عدد کوانتومی میتوانیم دقیقتر بدانیم الکترون کجا قرار دارد.
- مدل کوانتومی اتم از سال ۱۹۲۶ تا امروز با استفاده از خاصیت موجی الکترون، معادله شرودینگر، عدم قطعیت هایزنبرگ و اسپین همچنان کار میکند.
source