مشتق یک مفهوم مهم در حساب دیفرانسیل به حساب میآید. مشتق در واقع تغییرات یک تابع نسبت به تغییرات یک متغیر مستقل است. در این مطلب از مجله فرادرس مشتق ضرب دو تابع را معرفی و اثبات میکنیم. برای مشتق گرفتن از دو تابع که در هم ضرب شدهاند باید از تابع اول مشتق بگیریم و در تابع دوم ضرب کنیم سپس از تابع دوم مشتق میگیریم و در تابع اول ضرب میکنیم و در آخر این دو جمله را با هم جمع میکنیم. اگر به این موضوع علاقهمند هستید این مطلب را تا انتها مطالعه کنید. سپس با مثالهایی در ادامه این موضوع را تکمیل میکنیم. در آخر نیز تعریف مشتق و جدول قوانین مشتقگیری را ارائه خواهیم داد.
تعریف مشتق ضرب
اگر دو تابع $$f(x)$$ و $$g(x)$$ مشتق پذیر باشند، آنگاه مشتق ضرب این دو تابع به صورت زیر تعریف میشود:
$${left( {f(x),g(x)} right)^prime } = f'(x),g(x) + f(x),g'(x)$$
اثبات ضرب مشتق
با استفاده از تعریف مشتق میتوانیم ویژگی مشتق ضرب را اثبات کنیم.
$$h'(x) = lim_{Delta xto 0} frac{h(x+Delta x)-h(x)}{Delta x} $$
در عبارت فوق از تعریف مشتق برای تابع $$h(x)$$ استفاده شده است و بیانگر تغییرات تابع $$h(x)$$ نسبت به $$x$$ در نقطه $$x$$ هست.
$$= lim_{Delta xto 0} frac{f(x+Delta x)g(x+Delta x)-f(x)g(x)}{Delta x}$$
در عبارت بالا به جای تابع $$h(x)$$ از تابع $$ {f(x),g(x)} $$ استفاده شده است و تعریف حد در مشتق به آن اضافه شده است.
$$= lim_{Delta xto 0} frac{f(x+Delta x)g(x+Delta x)-f(x)g(x+Delta x)+f(x)g(x+Delta x)-f(x)g(x)}{Delta x}$$
برای جداسازی جملات عبارت $$f(x)g(x+Delta x)$$ را در صورت کسر فوق اضافه و کم میکنیم.
$$= lim_{Delta xto 0} frac{big[f(x+Delta x)-f(x)big] cdot g(x+Delta x) + f(x) cdot big[g(x+Delta x)-g(x)big]}{Delta x}$$
برای محاسبه حد نیاز است که جملات صورت را به نحوی مرتب کنیم که بتوانیم $$f(x)$$ را از جمله دوم و $$g(x+Delta x)$$ را از جمله اول فاکتور بگیریم.
$$= lim_{Delta xto 0} frac{f(x+Delta x)-f(x)}{Delta x} cdot {lim_{Delta xto 0} g(x+Delta x)} + lim_{Delta xto 0} f(x) cdot lim_{Delta xto 0} frac{g(x+Delta x)-g(x)}{Delta x}$$
در بالا توانستیم کسر را به دو قسمت تبدیل کنیم و حد را مستقل از $$Delta x$$ بگیریم. در اثبات فوق جمله $$lim_{Delta xto 0} {g(x+Delta x)}=g(x)$$، قضیهای است که طبق آن توابع مشتقپذیر پیوسته هستند.
$$= f'(x)g(x)+f(x)g'(x)$$
بنابراین توانستیم مشتق ضرب دو تابع را اثبات کنیم.
چگونه مشتق ضرب را محاسبه کنیم؟
به زبان ساده اگر بخواهیم از دو تابع که در یکدیگر ضرب شدهاند مشتق بگیریم، ابتدا باید از تابع اول مشتق بگیریم و در تابع دوم ضرب کنیم سپس از تابع دوم مشتق میگیریم و در تابع اول ضرب میکنیم در پایان جملات را با هم جمع میکنیم.

چطور مشتق ضرب را یاد بگیریم؟

برای آموختن روش مشتق ضرب ابتدا باید با مفاهیم پایه مانند تعریف مشتق، انواع توابع، عملیات جبری و غیره آشنا باشید. برای انجام دادن مشتق ضرب دو تابع باید مشتق تابع اول ضربدر تابع دوم را با مشتق تابع دوم ضربدر تابع اول جمع کنیم.
پس از یادگیری مشتق ضرب دو تابع میتوانید سایر قواعد مشتقگیری را یاد بگیرید و سپس کاربردهای مشتق در ریاضی را بیاموزید.
در مرحله بعد مفاهیم پیشرفتهتر مانند انتگرال را که عکس عمل مشتقگیری است را فراگیرید. در نهایت، با استفاده از فیلمهای آموزشی موجود در فرادرس میتوانید مشتق و حساب دیفرانسیل و انتگرال را به طور کامل یادبگیرید و با کاربردهای عملی آنها آشنا شود.
میتوانید فیلمهای آموزش مرتبط با مشتق در ریاضی را از لینکهای زیر در فرادرس مشاهده کنید.
همچنین فرادرس دروس کاربردی و متنوعی را در ریاضیات منتشر کرده است که اگر به این موضوع علاقهمند هستید میتوانید آنها را از طریق لینک زیر مشاهده کنید.

مشتق ضرب توابع چندجملهای
در این قسمت به بررسی مشتق ضرب توابعی که شامل چندجملهای هستند میپردازیم.
مثال اول مشتق ضرب توابع چندجملهای
میخواهیم مشتق عبارت $$y = sqrt[3]{{{x^2}}}left( {2x – {x^2}} right)$$ را حساب کنیم.
پاسخ:
ابتدا برای آسانتر شدن کار، رادیکال را به صورت توانی مینویسیم.
$$y = {x^{frac{2}{3}}}left( {2x – {x^2}} right)$$
مطابق فرمول ارائه شده باید ابتدا از تابع $${x^{frac{2}{3}}}$$ مشتق بگیریم و در تابع $$left( {2x – {x^2}} right)$$ ضرب کنیم سپس از تابع $$left( {2x – {x^2}} right)$$ مشتق میگیریم و در تابع $${x^{frac{2}{3}}}$$ ضرب میکنیم و در آخر این دو جمله را با هم جمع میکنیم.
$$y’ = frac{2}{3}{x^{ – frac{1}{3}}}left( {2x – {x^2}} right) + {x^{frac{2}{3}}}left( {2 – 2x} right)$$
در این مرحله سادهسازی میکنیم.
$$y’ = frac{4}{3}{x^{frac{2}{3}}} – frac{2}{3}{x^{frac{5}{3}}} + 2{x^{frac{2}{3}}} – 2{x^{frac{5}{3}}} = frac{{10}}{3}{x^{frac{2}{3}}} – frac{8}{3}{x^{frac{5}{3}}}$$
مثال دوم مشتق ضرب توابع چندجملهای
مشتق عبارت $$fleft( x right) = left( {6{x^3} – x} right)left( {10 – 20x} right)$$ را حساب کنید.
پاسخ:
با استفاده از فرمولی که در ابتدا گفته شد باید ابتدا از تابع $$left( {6{x^3} – x} right)$$ مشتق بگیریم و در تابع $$left( {10 – 20x} right)$$ ضرب کنیم سپس از تابع $$left( {10 – 20x} right)$$ مشتق میگیریم و در تابع $$left( {6{x^3} – x} right)$$ ضرب میکنیم و در پایان این دو جمله را با هم جمع میکنیم.
.
$$begin{align*}f’left( x right) & = left( {18{x^2} – 1} right)left( {10 – 20x} right) + left( {6{x^3} – x} right)left( { – 20} right)\ & = – 480{x^3} + 180{x^2} + 40x – 10end{align*}$$
مثال سوم مشتق ضرب توابع چندجملهای
میخواهیم مشتق عبارت $$fleft( t right) = left( {4{t^2} – t} right)left( {{t^3} – 8{t^2} + 12} right)$$ را حساب کنیم.
پاسخ:
همانطور که قبلا گفته شد ابتدا از تابع $$left( {4{t^2} – t} right)$$ مشتق میگیریم و در تابع $$left( {{t^3} – 8{t^2} + 12} right)$$ ضرب کنیم سپس از تابع $$left( {{t^3} – 8{t^2} + 12} right)$$ مشتق میگیریم و در تابع $$left( {4{t^2} – t} right)$$ ضرب میکنیم سپس این دو جمله را با هم جمع میکنیم.
$$f’left( t right) = left( {8t – 1} right)left( {{t^3} – 8{t^2} + 12} right) + left( {4{t^2} – t} right)left( {3{t^2} – 16t} right) = 20{t^4} – 132{t^3} + 24{t^2} + 96t – 12$$
مثال چهارم مشتق ضرب توابع چندجملهای
مشتق عبارت $$y = left( {1 + sqrt {{x^3}} } right),left( {{x^{ – 3}} – 2sqrt[3]{x}} right)$$ را حساب کنید.
پاسخ:
ابتدا برای آسانتر شدن کار، رادیکال را به صورت توانی مینویسیم.
$$y = left( {1 + {x^{frac{3}{2}}}} right),left( {{x^{ – 3}} – 2{x^{frac{1}{3}}}} right)$$
مطابق فرمول ارائه شده باید ابتدا از تابع $$left( {1 + {x^{frac{3}{2}}}} right)$$ مشتق بگیریم و در تابع $$left( {{x^{ – 3}} – 2{x^{frac{1}{3}}}} right)$$ ضرب کنیم سپس از تابع $$left( {{x^{ – 3}} – 2{x^{frac{1}{3}}}} right)$$ مشتق میگیریم و در تابع $$left( {1 + {x^{frac{3}{2}}}} right)$$ ضرب میکنیم و در مرحله بعد این دو جمله را با هم جمع میکنیم.
$$frac{{dy}}{{dx}} = left( {frac{3}{2}{x^{frac{1}{2}}}} right),left( {{x^{ – 3}} – 2{x^{frac{1}{3}}}} right) + left( {1 + {x^{frac{3}{2}}}} right),left( { – 3{x^{ – 4}} – frac{2}{3}{x^{ – ,,frac{2}{3}}}} right) = – 3{x^{ – 4}} – frac{3}{2}{x^{ – ,,frac{5}{2}}} – frac{2}{3}{x^{ – ,,frac{2}{3}}} – frac{{11}}{3}{x^{frac{5}{6}}}$$
مثال پنجم مشتق ضرب توابع چندجملهای
میخواهیم مشتق عبارت $$hleft( z right) = left( {1 + 2z + 3{z^2}} right)left( {5z + 8{z^2} – {z^3}} right)$$ را حساب کنیم.
پاسخ:
با استفاده از فرمولی که در ابتدا معرفی شد باید از تابع $$left( {1 + 2z + 3{z^2}} right)$$ مشتق بگیریم و در تابع $$left( {5z + 8{z^2} – {z^3}} right)$$ ضرب کنیم سپس از تابع $$left( {5z + 8{z^2} – {z^3}} right)$$ مشتق میگیریم و در تابع $$left( {1 + 2z + 3{z^2}} right)$$ ضرب میکنیم و در آخر این دو جمله را با هم جمع میکنیم.
$$begin{align*}h’left( z right) & = left( {2 + 6z} right)left( {5z + 8{z^2} – {z^3}} right) + left( {1 + 2z + 3{z^2}} right)left( {5 + 16z – 3{z^2}} right)\ & = 5 + 36z + 90{z^2} + 88{z^3} – 15{z^4}end{align*}$$
مثال ششم مشتق ضرب توابع چندجملهای
میخواهیم مشتق عبارت $${f}(x)=(3x-2x^2)(5+4x)$$ را حساب کنیم.
پاسخ:
در این مثال دو تابع $$(3x-2x^2)$$ و $$(5+4x)$$ در یکدیگر ضرب شدهاند. به راحتی میتوانیم با استفاده از فرمول ارائه شده مشتق این عبارت را محاسبه کنیم. یعنی باید از تابع $$(3x-2x^2)$$ مشتق بگیریم و در تابع $$(5+4x)$$ ضرب کنیم سپس از تابع $$(5+4x)$$ مشتق میگیریم و در تابع $$(3x-2x^2)$$ ضرب میکنیم سپس این دو جمله را با هم جمع میکنیم.
$$f’(x) = (5 + 4x)(3 – 4x)+(3x – 2x^2) = 15 + 12x – 20x – 16x^2+12x – 8x^2$$
بنابراین با ساده کردن عبارت خواهیم داشت:
$$ f’(x) =-24x^2 + 4x + 15 $$
مثال هفتم مشتق ضرب توابع چندجملهای
مشتق عبارت $${g}(x)=2x(x^2+3x)$$ را حساب کنید.
پاسخ:
با استفاده از فرمول ارائه شده در این مطلب میتوانیم مشتق عبارت فوق را محاسبه کنیم. بنابراین از تابع $$2x$$ مشتق میگیریم و در تابع $$(x^2+3x)$$ ضرب میکنیم سپس از تابع $$(x^2+3x)$$ مشتق میگیریم و در تابع $$2x$$ ضرب میکنیم در مرحله بعدی این دو جمله را با هم جمع میکنیم.
$$g’(x) = 2(x^2 + 3x)+2x(2x + 3) = 2x^2 + 6x+4x^2 + 6x$$
با سادهسازی مقدار نهایی را محاسبه میکنیم.
$$g’(x) = 6x^2 +12x$$
مثال هشتم مشتق ضرب توابع چندجملهای
میخواهیم مشتق عبارت $${h}(x)=(frac{1}{x}+1)(x-1)$$ را حساب کنیم.
پاسخ:
در این مثال برای راحتی عبارت کسری را به صورت توان نوشته و کل عبارت را بازنویسی میکنیم.
$$h(x) = (x^{-1} + 1)(x – 1)$$
سپس با استفاده از فرمول ارائه شده در این ابتدای این مطلب میتوانیم مشتق عبارت را حساب کنیم. در نتیجه از تابع $$(x^{-1} + 1)$$ مشتق میگیریم و در تابع $$(x – 1)$$ ضرب میکنیم سپس از تابع $$(x – 1)$$ مشتق میگیریم و در تابع $$(x^{-1} + 1)$$ ضرب میکنیم در پایان این دو جمله را با هم جمع میکنیم.
$$h’(x) =(x – 1)(-x^{-2})+ (x^{-1} + 1)(1) = – x^{-1} + x^{-2}+x^{-1} + 1$$
بنابراین با ساده کردن عبارت خواهیم داشت:
$$ h’(x) = 1 + x^{-2} = frac{x2+1}{x2}$$
مثال نهم مشتق ضرب توابع چندجملهای
مشتق عبارت $${f}(x)=3(x^4-1)(5x^2+2x)$$ را حساب کنید.
پاسخ:
در این مثال دو تابع $$(x^4-1)$$ و $$(5x^2+2x)$$ در یکدیگر ضرب شدهاند و میتوانیم با استفاده از فرمول ارائه شده در ابتدای این مطلب، مشتق این عبارت را محاسبه کنیم. بدین منظور از تابع $$(x^4-1)$$ مشتق میگیریم و در تابع $$(5x^2+2x)$$ ضرب میکنیم سپس از تابع $$(5x^2+2x)$$ مشتق میگیریم و در تابع $$(x^4-1)$$ ضرب میکنیم سپس این دو جمله را با هم جمع میکنیم.
$$f’(x) = 3[(5x^2 + 2x)(4x^3)+(x^4 – 1)(10x + 2) ] = 3( 20x^5 +8 x^4+10x^5 + 2x^4 – 10x- 2 )$$
در نتیجه با ساده کردن عبارت خواهیم داشت:
$$f’(x) = 3(30 x^5 +10 x^4 -10 x -2)$$

مشتق ضرب توابع مثلثاتی
مثالهایی برای مشتق توابع مثلثاتی در این قسمت ارائه خواهد شد.
مثال اول مشتق ضرب توابع مثلثاتی
مشتق عبارت $${g}(x)=xcos x$$ را حساب کنید.
پاسخ:
در این مثال دو تابع $$x$$ و $$cos x$$ در یکدیگر ضرب شدهاند. به راحتی میتوانیم با استفاده از فرمول ارائه شده مشتق این عبارت را محاسبه کنیم. یعنی از تابع $$x$$ مشتق میگیریم و در تابع $$cos x$$ ضرب میکنیم سپس از تابع $$cos x$$ مشتق میگیریم و در تابع $$x$$ ضرب میکنیم در آخر این دو جمله را با هم جمع میکنیم.
$$acute{g}(x)=cos xtimes 1+xtimes(-sin x)$$
در نتیجه با ساده کردن عبارت خواهیم داشت:
$$acute{g}(x)=cos x-xsin x$$
مثال دوم مشتق ضرب توابع مثلثاتی
مشتق عبارت $${f}(x)=(1-2x)sin x $$ را حساب کنید.
پاسخ:
همانطور که قبلا گفته شد باید ابتدا از تابع $$(1-2x)$$ مشتق بگیریم و در تابع $$sin x$$ ضرب کنیم سپس از تابع $$sin x$$ مشتق میگیریم و در تابع $$(1-2x)$$ ضرب میکنیم و مجموع این دو جمله را حساب میکنیم.
$$acute{f}(x)=sin x times (-2)+(1-2x)timescos x$$
در نتیجه با ساده کردن عبارت خواهیم داشت:
$$acute{f}(x)=-2sin x +cos x-2xcos x$$
مشتق ضرب توابع نمایی و لگاریتمی
در این بخش مثالهای برای مشتق ضرب توابع لگاریتمی و نمایی ارائه میشود.
مثال اول مشتق ضرب توابع نمایی و لگاریتمی
میخواهیم مشتق عبارت $$f(x)=x log x$$ را حساب کنیم.
پاسخ:
در این مثال دو تابع $$x$$ و $$log x$$ در هم ضرب شدهاند و میخواهیم با استفاده از فرمول مشتق ضرب، مشتق این عبارت را حساب کنیم. برای انجام این کار باید ابتدا از تابع $$x$$ مشتق بگیریم و در تابع $$log x$$ ضرب کنیم سپس از تابع $$log x$$ مشتق میگیریم و در تابع $$x$$ ضرب میکنیم سپس جملات را با هم جمع میکنیم.
$$acute{f}(x)= log x+xtimes (frac{1}{x})$$
بنابراین با ساده کردن عبارت خواهیم داشت:
$$acute{f}(x)= log x+1$$
مثال دوم مشتق ضرب توابع نمایی و لگاریتمی
میخواهیم مشتق عبارت $$h(x)=x^2 log x$$ را حساب کنیم.
پاسخ:
با استفاده از فرمول ارائه شده در این مطلب میتوانیم مشتق عبارت فوق را محاسبه کنیم. در نتیجه از تابع $$x^2$$ مشتق میگیریم و در تابع $$log x$$ ضرب میکنیم و بعد از تابع $$log x$$ مشتق میگیریم و در تابع $$x^2$$ ضرب میکنیم در پایان جملات را با هم جمع میکنیم.
$$acute{h}(x)=log x times(2x)+x^2times (frac{1}{x})$$
بنابراین با ساده کردن عبارت فوق به نتیجه زیر میرسیم:
$$acute{h}(x)=2x log x+x $$
مثال سوم مشتق ضرب توابع نمایی و لگاریتمی
میخواهیم مشتق عبارت $$y=(1-x^3)e^{2x}$$ را حساب کنیم.
پاسخ:
با استفاده از فرمول ارائه شده در این مطلب میتوانیم مشتق عبارت فوق را محاسبه کنیم. بنابراین باید ابتدا از تابع $$(1-x^3)$$ مشتق بگیریم و در تابع $$e^{2x}$$ ضرب کنیم همچنین از تابع $$e^{2x}$$ مشتق میگیریم و در تابع $$(1-x^3)$$ ضرب میکنیم بعد باید این دو جمله را با هم جمع کنیم.
$$frac{dy}{dx} = e^{2x} times (-3x^2)+(1-x^3) times 2e^{2x} = e^{2x}(2-3x^2-2x^3)$$
مثال چهارم مشتق ضرب توابع نمایی و لگاریتمی
مشتق عبارت $$y=x^3(4-x)^{frac{1}{2}}$$ را حساب کنید.
پاسخ:
در این مثال دو تابع $$x^3$$ و $$(4-x)^{frac{1}{2}}$$ در یکدیگر ضرب شدهاند. برای محاسبه مشتق ضرب این عبارت باید از تابع $$x^3$$ مشتق بگیریم و در تابع $$(4-x)^{frac{1}{2}}$$ ضرب کنیم سپس از تابع $$(4-x)^{frac{1}{2}}$$ مشتق میگیریم و در تابع $$x^3$$ ضرب میکنیم در نهایت، این دو جمله را با هم جمع میکنیم.
$$frac{dy}{dx} = (3x^2)(4 – x)^{frac{1}{2}} + x^3left(-frac{1}{2}(4 – x)^{-frac{1}{2}}right)= 3x^2(4 – x)^{frac{1}{2}} – frac{1}{2}x^3(4 – x)^{-frac{1}{2}}$$
نکته: اگر بیش از دو تابع برای مشتقگیری همزمان داشتیم مثلا سه یا چهار تابع، میتوانیم از روبط زیر استفاده کنیم:
$$begin{align*}{left( {f,g,h} right)^prime } & = f’,g,h + f,g’,h + f,g,h’\ & {left( {f,g,h,w} right)^prime } = f’,g,h,w + f,g’,h,w + f,g,h’,w + f,g,h,w’end{align*}$$

حل مسائل مشتق ضرب با تعریف مشتق
در اینجا مثالهای خاصی مطرح میشوند که با استفاده از تعریف مشتق قابل حل هستند. البته در مطالب قبلی مجله فرادرس نیز به مشتق و محاسبات آن اشاره کردهایم که با مطالعه مطلب مربوطه میتوانید اطلاعات بیشتری کسب کنید.
مثال اول مشتق ضرب با تعریف مشتق
اگر موارد زیر را داشته باشیم:
$$fleft( 2 right) = – 8$$
$$f’left( 2 right) = 3$$
$$gleft( 2 right) = 17$$
$$g’left( 2 right) = – 4$$
آنگاه مشتق عبارت $${left( {f,g} right)^prime }left( 2 right)$$ را حساب کنید.
پاسخ:
از رابطه مشتق ضرب داشتیم:
$${left( {f,g} right)^prime }left( x right) = f’left( x right)gleft( x right) + fleft( x right)g’left( x right)$$
اکنون میتوانیم دادههای سوال را در رابطه فوق جایگذاری کنیم.
$${left( {f,g} right)^prime }left( 2 right) = f’left( 2 right)gleft( 2 right) + fleft( 2 right)g’left( 2 right)$$
با سادهسازی مقدار نهایی را محاسبه میکنیم.
$${left( {f,g} right)^prime }left( 2 right) = left( 3 right)left( {17} right) + left( { – 8} right)left( { – 4} right) = require{bbox} bbox[2pt,border:1px solid black]{{83}}$$
مثال دوم مشتق ضرب با تعریف مشتق
موارد زیر را در اختیار داریم:
$$fleft( x right) = {x^3}gleft( x right)$$
$$gleft( { – 7} right) = 2$$
$$g’left( { – 7} right) = – 9$$
عبارت $$f’left( { – 7} right)$$ را حساب کنید.
پاسخ:
در این مثال مقدار $$g(x)$$ را نداریم اما با استفاده از فرمول مشتق ضرب دو تابع میتوانیم مشتق $$f(x)$$ را محاسبه کنیم.
$$f’left( x right) = 3{x^2}gleft( x right) + {x^3}g’left( x right)$$
در مرحله بعد کافی است تا $$x = – 7$$ را در رابطه فوق قرار دهیم و با اطلاعات داده شده مقدار $$f’left( { – 7} right)$$ را حساب کنیم.
$$f’left( { – 7} right) = 3{left( { – 7} right)^2}gleft( { – 7} right) + {left( { – 7} right)^3}g’left( { – 7} right) = 3left( {49} right)left( 2 right) + left( { – 343} right)left( { – 9} right) = require{bbox} bbox[2pt,border:1px solid black]{{3381}}$$
مثال سوم مشتق ضرب با تعریف مشتق
عبارت $$Vleft( t right) = left( {4 – {t^2}} right)left( {1 + 5{t^2}} right)$$ در کدام ناحیه در حال افزایش و در کدام ناحیه در حال کاهش است؟
پاسخ:
مشتق توابع نرخ تغییرات آن را مشخص میکند بدین منظور از فرمول مشتق ضرب برای عبارت فوق استفاده میکنیم.
$$require{bbox} bbox[2pt,border:1px solid black]{{V’left( t right) = left( { – 2t} right)left( {1 + 5{t^2}} right) + left( {4 – {t^2}} right)left( {10t} right) = 38t – 20{t^3} = 2tleft( {19 – 10{t^2}} right)}}$$
در مرحله بعد باید تعیین کنیم که تابع در کدام ناحیه بدون تغییر است، در واقع آن را تعیین علامت میکنیم. بدین منظور مشتق تابع را برابر صفر قرار میدهیم و آن را حل میکنیم. بنابراین مشتق تابع در نقاط زیر صفر خواهد شد:
$$require{bbox} bbox[2pt,border:1px solid black]{{t = 0 hspace{0.5in} t = pm sqrt {frac{{19}}{{10}}} = pm 1.3784}}$$
برای پاسخ دادن به این سوال باید تعیین کنیم که مشتق در کجا مثبت (تابع در حال افزایش) است و در کجا منفی (تابع در حال کاهش) است. چون مشتق این تابع پیوسته است، تابع در نقاطی تغییر علامت میدهد که مشتق تابع برابر صفر باشد. بدین منظور مطابق شکل به مشتق تابع عدد میدهیم تا آن را تعیین علامت کنیم.
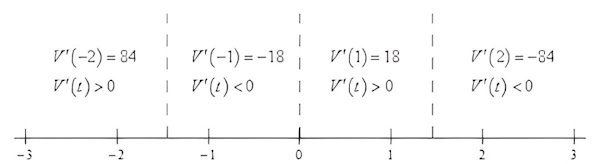
با استفاده از اطلاعات شکل فوق میتوانیم تعیین کنیم که تابع مورد نظر در چه محدودهای افزایشی و در چه محدودهای کاهشی است.
تابع در حال افزایش:
$$- infty < t < – sqrt {frac{{19}}{{10}}} ,,,,,,,0 < t < sqrt {frac{{19}}{{10}}}$$
تابع در حال کاهش:
$$- sqrt {frac{{19}}{{10}}} < t < 0,,,,,sqrt {frac{{19}}{{10}}} < t < infty $$

جدول مشتق
در این قسمت به صورت خلاصه قوانین مشتق مرور شدهاند. در این قسمت دو تابع $$f(x)$$ و $$g(x)$$ مشتق پذیر هستند و $$c$$ عدد ثابت است.
قوانین عمومی
در این قسمت برخی قوانین عمومی که در مشتق ضرب مورد نیاز است ارائه شده است.
| پاسخ | مشتق |
| $$c cdot frac{df}{dx}$$ | $$frac{d}{dx}(c cdot f)$$ |
| $$fcdotfrac{dg}{dx} + gcdotfrac{df}{dx}$$ | $$frac{d}{dx}(fcdot g)$$ |
| $$frac{df}{dg}cdotfrac{dg}{dx} = f’(g(x)) times g’(x)$$ | $$frac{d}{dx}[f(g(x))]$$ |
| $$sum_{i=0}^{n} {nchoose i} f^{n-i}(x)g^{i}(x)$$ | $$frac{d^n}{dx^n} f(x)g(x)$$ |
| $$-frac{acute{f}}{f^2}$$ | $$frac{d}{dx}(frac{1}{f})$$ |
قوانین چندجملهای و توان
در اینجا قوانین مشتق توابع چندجملهای و توانی که ممکن است در مشتق ضرب به کار رفته باشند، معرفی شدهاند.
| پاسخ | مشتق |
| $$0$$ | $$frac{d}{dx}(c)$$ |
| $$1$$ | $$frac{d}{dx} x$$ |
| $$nx^{n-1}$$ | $$frac{d}{dx} x^n$$ |
| $$frac{1}{2sqrt{x}}$$ | $$frac{d}{dx} sqrt{x}$$ |
| $$ -frac{1}{x^2}$$ | $$frac{d}{dx} frac{1}{x}$$ |
قوانین توابع مثلثاتی
در این بخش مشتق توابع مثلثاتی مرور شدهاند.
| پاسخ | مشتق |
| $$cos(x)$$ | $$frac{d}{dx} sin(x)$$ |
| $$-sin(x) $$ | $$frac{d}{dx} cos(x)$$ |
| $$sec^2(x)$$ | $$frac{d}{dx} tan(x)$$ |
| $$ -csc^2(x)$$ | $$frac{d}{dx} cot(x)$$ |
| $$sec(x)tan(x)$$ | $$frac{d}{dx} sec(x)$$ |
| $$ -csc(x)cot(x)$$ | $$frac{d}{dx} csc(x)$$ |
قوانین توابع نمایی و لگاریتمی
در جدول زیر مشتق توابع نمایی و لگاریتمی که ممکن است در مشتق ضرب وجود داشته باشند معرفی شدهاند.
| پاسخ | شرط | مشتق |
| $$ e^x$$ | ندارد | $$frac{d}{dx} e^x$$ |
| $$a^x ln(a)$$ | $$a > 0$$ | $$frac{d}{dx} a^x $$ |
| $$frac{1}{x}$$ | ندارد | $$frac{d}{dx} ln(x)$$ |
| $$frac{1}{xln(a)}$$ | $$ a > 0, aneq 1$$ | $$ frac{d}{dx} log_a (x)$$ |
| $$ f^gleft( f’frac{g}{f} + g’ln(f)right)$$ | $$f > 0$$ | $$frac{d}{dx} (f^g)$$ |
| $$c^f f’ ln c$$ | ندارد | $$frac{d}{dx}(c^f)$$ |
نتیجهگیری
محاسبه مشتق دو تابع که در یکدیگر ضرب شدهاند بسیار ساده است. در این مطلب از مجله فرادرس مشتق ضرب معرفی و اثبات شد. به طور ساده برای مشتق گرفتن از دو تابع که در یکدیگر ضرب شدهاند باید مجموع مشتق تابع اول ضربدر تابع دوم و مشتق تابع دوم ضربدر تابع اول را حساب کنیم. همچنین در آخر تعریف کلی مشتق و جدول قوانین مشتقگیری نیز ارائه شد.
source