نوسان و موج در تمام ابعاد زندگی ما جریان دارد. از نمونه‌های آن می‌توان به امواج دریا، امواج صوتی، ارتعاش اتم‌ها در مولکول و ضربان قلب را مثال زد که همگی از قوانین نوسان پیروی می‌کنند. در واقع نوسان، حرکت رفت و برگشتی بین دو نقطه ثابت است. نیرو و انرژی ویژگی مشترک بین تمام دستگاه‌های نوسانگر است. در این مطلب از مجله فرادرس به معرفی انواع موج و نوسان و همچنین مشخصات آن‌ها پرداخته خواهد شد. اگر به این موضوع علاقه‌مند هستید این مطلب را تا انتها مطالعه کنید.

نوسان و موج چیست؟

نوسان نوعی از حرکت متناوب است. یک نوسان معمولا به صورت تغییرات متناوب در زمان هست. نوسان می‌تواند بین نقطه تعادل یا دو حالت یک سیستم رخ دهد که آونگ را می‌توان مثال خوبی از حرکت نوسانی دانست. نوسانات معمولا سینوسی هستند.

قانون هوک

قانون اول نیوتون اشاره به این موضوع دارد که اگر به جسمی نیرو وارد نشود اگر ثابت باشد ثابت باقی می‌ماند و اگر  درحال حرکت باشد به حرکت خود در مسیر مستقیم با سرعت ثابت ادامه خواهد داد. اما اگر به جسم نیروی خارجی اعمال شود ممکن است که حرکتش رفت و برگشتی (نوسانی) شود. مطابق شکل زیر یک خطکش را درنظر بگیرید که به یک سمت خم شده که وقتی که رها می‌شود به سمت مخالف آن بازمی‌گردد. نیرویی که برخلاف نیروی وارد شده بر جسم باعث تغییر شکل می‌شود به اصطلاح «نیروی مقاوم» (Restoring Force) گویند. در مبحث نوسان و موج، همان‌طور که گفته شد اگر یک خطکش را پس از خم کردن رها کنیم آنقدر حرکت نوسانی انجام می‌دهد تا به نقطه تعادل پایدار خود برگردد. جایی که برآیند نیروی وارده بر آن صفر باشد. به این نوع حرکت، حرکت نوسانی میرا می‌گویند زیرا با گذشت زمان سیستم از حرکت می‌ایستد و نیرو صفر می‌شود که در این مورد در ادامه مطلب بیشتر بحث خواهد شد.

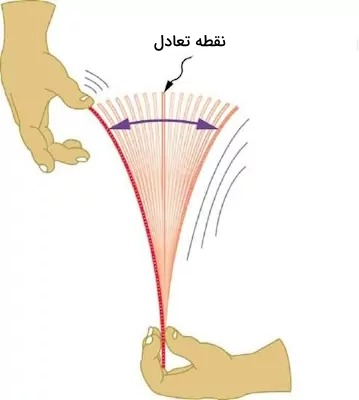
ساده‌ترین حرکت نوسانی زمانی رخ می‌دهد که نیروی مقاوم به طور مستقیم با جابجایی متناسب باشد. رابطه بین نیرو و جابجایی طبق قانون هوک به صورت زیر تعریف می‌شود:

$$F=-kx$$

عوامل به کار رفته در رابطه فوق به شرح زیر است:

• $$F$$: نیروی مقاوم
• $$k$$: ضریب ثابت که میزان سختی برای از تعادل خارج کردن سیستم است
• $$x$$: جابجایی از حالت تعادل

نکته: علامت منفی در قانون هوک به این معنا است که نیروی مقاوم خلاف جهت جابجایی است.

ضریب ثابت k به سختی آن سیستم بستگی دارد. هر چقدر ضریب k بزرگتر باشد، نیروی مقاوم و در نتیجه سختی سیستم نیز بیشتر است. واحد ضریب k، نیوتن بر متر (N/m) است.

مثال اول قانون هوک

وقتی شخصی با جرم ۸۰ کیلوگرم در یک خودرو می‌نشیند، فنرهای خودرو به اندازه ۱٫۲ سانتی‌متر فشرده می‌شوند. ضریب ثابت k را برای این سیستم حساب کنید.

پاسخ

اگر نقطه تعادل را $$x=0$$ فرض کنیم هنگامی که شخص داخل خودرو می‌نشیند، فنرهای خودرو به اندازه ۱٫۲ سانتی‌متر فشرده می‌شوند یعنی جابجایی از نقطه تعادل $$x = -1.20 times 10^{-2} m$$ است. در این لحظه فنرهای خودرو یک نیروی مقاوم F برابر جرم شخص و در خلاف جهت آن به اندازه $$w = mg = (80.0 , kg)(9.80 , m/s^2) = 784 , N.$$ وارد می‌کنند. در این مثال باید از قانون هوک برای محاسبه ضریب ثابت k استفاده کنیم.

$$k = -dfrac{F}{x}. nonumber$$

$$begin{align*} k &= -dfrac{784 , N}{-1.20 times 10^{-2}m} \[5pt] &=6.53 times 10^4 , N/m.end{align*}$$

انرژی در قانون هوک

برای تغییر شکل در یک سیستم کار باید انجام داد. پس نیرو باید در جهت جابجایی اعمال شود.برای مثال اگر تغییر شکل  فقط به صورت فشرده شدن فنر یک خودرو باشد و هیچ مقداری از کار به صورت گرما، صدا یا انرژی مکانیکی تبدیل نشود آنگاه تمام کاری که منجر به تغییر شکل سیستم شده به صورتی از انرژی پتانسیل در آن ذخیره می‌شود. در مبحث نوسان و موج، انرژی پتانسیل ذخیره شده در فنر به صورت زیر است:

$$PE_{el} = dfrac{1}{2}kx^2$$

عوامل به کار رفته در رابطه فوق به شرح زیر است:

• $$PE_{el}$$: انرژی پتانسیل آلاستیک نام دارد که از قانون هوک پیروی می‌کند
• k: ضریب ثابت
• x: جابجایی از حالت تعادل

طبق قانون کار و انرژی، برای یافتن انرژی ذخیره شده در سیستم می‌توان کار انجام انجام شده برای تغییر شکل سیستم را محاسبه کرد. این کار به وسیله نیروی اعمال شده $$F_{app}$$ انجام شده است. نیروی اعمال شده دقیقا هم اندازه و خلاف جهت نیروی مقاوم است بنابراین:

$$F_{app} = kx$$

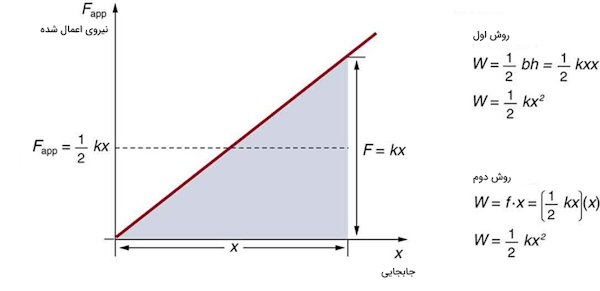
در شکل زیر نمودار نیروی اعمال شده بر میزان جابجایی برای سیستمی که مطابق قانون هوک تعریف می‌شود، رسم شده است. کار انجام شده سیستم برابر ضرب نیرو در جابجای است که برابر مساحت زیر نمودار شکل زیر است. روش دیگری که می‌توان با آن کار را تعریف کرد این است که نیرو به صورت خطی از صفر تا $$kx$$ افزایش پیدا می‌کند بنابراین میانگین نیرو برابر $$(1/2)kx$$ است.

$$W = F_{app} d = [(1/2)kx](x) = (1/2)kx^2$$

دوره تناوب و فرکانس در حرکت نوسان

در مبحث نوسان و موج، حرکت تناوبی یا دوره‌ای به حرکتی گفته می‌شود که در فواصل زمانی منظم تکرار می‌شود مانند حرکت سیم یک گیتار یا بالا و پایین شدن یک فنر. زمان لازم برای کامل شدن یک نوسان را دوره تناوب یا پریود می‌گویند و با $$T$$ نمایش می‌دهند که واحد آن نیز ثانیه است. مفهوم دیگری که با دوره تناوب در ارتباط است فرکانس است. فرکانس عبارت است از تعداد رویداد (در اینجا نوسان) در واحد زمان است که آن را با نماد $$f$$ نمایش می‌دهند. رابطه بین فرکانس و دوره تناوب به صورت زیر است:

$$f = dfrac{1}{T}$$

واحد فرکانس چیست؟

واحد فرکانس در سیستم SI، هرتز تعریف شده است و هر هرتز عکس ثانیه است.

$$ Hz = dfrac{1}{s}$$

حرکت هماهنگ ساده

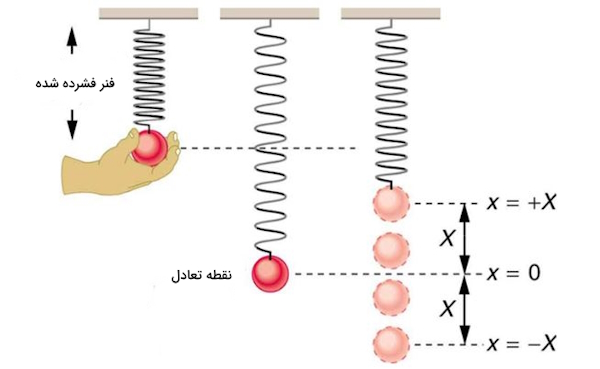
«حرکت هماهنگ ساده» (Simple Harmonic Motion) که به اختصار (SHM) نیز نوشته می‌شود عبارت است از حرکت نوسانی که در آن نیروی خالص با قانون هوک تعریف شود. اگر نیروی خالص با قانون هوک تعریف شود و هیچ‌گونه میرایی در سیستم وجود نداشته باشد، آنگاه نوسان هماهنگ ساده با جابجایی یکسان حول نقطه تعادل خود جابجا می‌شود. مطابق شکل زیر، بیشترین اندازه جابجایی حول نقطه تعادل را دامنه $$X$$ گویند. در مبحث نوسان و موج، واحد جابجایی و دامنه نوسان یکسان است ولی به نوع نوسانگر بستگی دارد. برای نمونه واحد دامنه و جابجایی در فنر یکسان است اما در صوت این‌گونه نیست زیرا دامنه که بیشینه جابجایی است به انرژی نوسانگر نیز مربوط است.

نکته مهم نوسانگر هماهنگ ساده در این است که فرکانس و دوره تناوب مستقل از دامنه هستند. برای مثال یک گیتار می‌تواند فرکانس ثابتی داشته باشد فارق از اینکه آرام یا سخت مرتعش شده باشد به خاطر این که دوره تناوب آن ثابت است. دوره تناوب به میزان سختی یک سیستم بستگی دارد. هرچقدر سیستم سختی بیشتری داشته باشد ضریب سختی بیشتری نیز دارد در نتیجه دوره تناوب کوتاه‌تری خواهد داشت. دوره تناوب همچنین به جرم سیستم نیز بستگی دارد، هرچقدر جرم سیستم بیشتر باشد دوره تناوب آن نیز طولانی‌تر خواهد بود. در حقیقت ضریب سختی $$k$$ و جرم، تنها کمیت‌هایی هستند که فرکانس و دوره تناوب به آن‌ها وابسته هستند. به طور خلاصه دوره تناوب نواسنگر هماهنگ ساده به صورت زیر است:

$$T = 2pi sqrt{dfrac{m}{k}}$$

و رابطه فرکانس نیز به شکل زیر است:

$$f = dfrac{1}{2pi} sqrt{dfrac{k}{m}}.$$

مثال اول حرکت هماهنگ ساده

ضریب سختی فنر یک خودرو $$k=6.53 times 10^4 , N/m$$ است و جرم خودرو ۹۰۰ کیلوگرم هست در جاده‌ای ناهموار حرکت می‌کند. فرکانس و دوره تناوب آن را حساب کنید.

پاسخ

با توجه به اینکه فرکانس و دوره تناوب فقط به جرم و ضریب ثابت $$k$$ وابسته هستند می‌توانیم از روابطی که در بالا گفته شد استفاده کنیم.

$$f = dfrac{1}{2pi} sqrt{dfrac{k}{m}} = dfrac{1}{2pi} sqrt{dfrac{6.53 times 10^4 , N/m}{900 , kg}}. nonumber$$

$$dfrac{1}{2pi} sqrt{72.6/s^{-2}} = 1.3656/s^{-1} approx 1.36/s^{-1} = 1.36 , Hznonumber$$

$$T = dfrac{1}{f} = dfrac{1}{1.356 , Hz} = 0.738 , s.nonumber$$

رابطه بین نوسانگر هماهنگ ساده و امواج

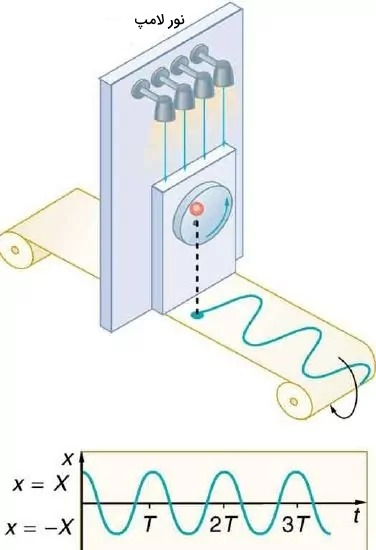
اگر مطابق شکل زیر حرکت یک نوسانگر هماهنگ ساده را در طول زمان اندازه‌گیری و ثبت کنیم یک موج سینوسی خواهیم داشت.

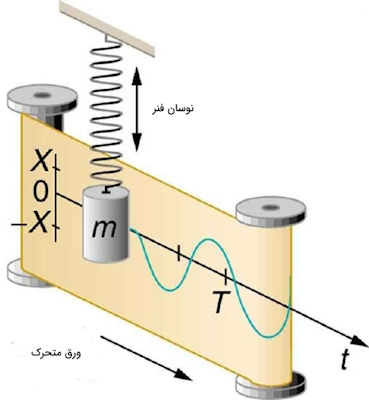
اگر نیروی مقاوم توسط قانون هوک تعریف شود آنگاه جابجایی در هر نوسانگر هماهنگ ساده، تابع وابسته به زمان خواهد شد:

$$x(t) = X , cos dfrac{2pi t}{T}$$

در رابطه فوق $$X$$ دامنه است. سرعت نوسانگر را می توانیم با مشتق گرفتن از رابطه مکان که در بالا ذکر شد بدست آوریم.

$$v(t) = -v_{max}sin left(dfrac{2pi t}{T}right)$$

علامت منفی در این رابطه برای اصلاح جهت سرعت است. در ابتدای حرکت یک متحرک علامت سرعت منفی است زیرا سیستم تمایل دارد که به حالت تعادل قبلی خود بازگردد.

بیشینه سرعت به صورت زیر است:

$$v_{max} = 2pi X/T = X sqrt{k/m}$$

نکته: متحرک در بیشینه جابجایی دارای سرعت صفر است.

شتاب یک نوسانگر را می‌توانیم از قانون دوم نیوتن و مشتق گرفتن از رابطه سرعت به صورت زیر بدست آوریم:

$$a = F/m = kx/m$$

$$a(t) = -dfrac{kX}{m}cos dfrac{2pi t}{T}.$$

نکته: شتاب نوسانگر از لحاظ اندازه متناسب با جابجای آن ولی در خلاف جهت آن است.

آونگ ساده

در مبحث نوسان و موج، آونگ ساده یک نمونه ساده و کاربردی از نوسانگر هماهنگ ساده است. یک آونگ ساده متشکل از یک جسم با جرم کم که به وسیله یک نخ یا ریسمان که بدون جرم آن را فرض می‌کنیم، آویزان شده و مطابق شکل زیر حرکت می‌کند. البته پیش‌تر در مطالب مجله فرادرس به آونگ ساده و مرکب و آونگ غیرخطی نیز اشاره کرده‌ایم که برای آشنایی بیشتر می‌توانید مطالب مربوطه را مطالعه کنید.

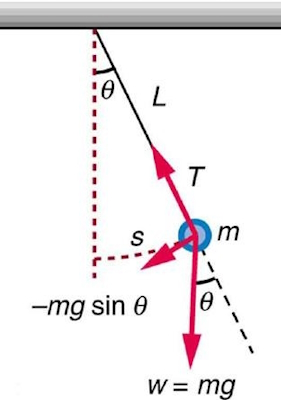
جابجایی آونگ مانند یک قوس است که در شکل فوق با $$S$$ نشان داده شده است. نیروی خالص وارده بر وزنه مماس بر قوس و برابر $$mg , sin , theta$$ است. (نیروی وزن mg دارای دو مولفه $$mg , cos , theta$$ در امتداد نخ و همچنین مولفه $$mg , sin , theta$$ مماس بر قوس است.) تنش نخ نیروی مولفه $$mg , cos theta$$ که موازی با نخ است را خنثی می‌کند. این باعث می‌شود که نیروی مقاوم خالص وزنه را به حالت تعادل خود در $$theta = 0$$ برگرداند.

برای اثبات حرکت نوسانی هماهنگ ساده در آونگ باید تناسب جابجایی با نیروی مقاوم را ثابت کنیم. برای این منظور از روش هم‌ارزی در حد استفاده می‌کنیم که در زوایای کوچک (کمتر از ۱۵ درجه)، $$sin , theta approx theta , (sin , theta)$$ است. بنابراین نیروی مقاوم به صورت زیر است:

$$F approx -mgtheta.$$

جابجایی $$S$$ به طور مستقیم با $$theta$$ ارتباط دارد. اگر $$theta$$ رادیان باشد آنگاه طول قوس به وسیله رابطه زیر با زاویه شعاعش در ارتباط است.

$$s = Ltheta$$

بنابراین:

$$theta = dfrac{s}{L}.$$

برای زوایای کوچک رابطه برای نیروی مقاوم به شکل زیر است:

$$F approx -dfrac{mg}{L}s.$$

از قبل برای نیروی مقاوم رابطه زیر را داشتیم:

$$F = -kx$$

نتیجه می‌گیریم:

$$k = mg/L$$

$$x=s$$

بنابراین اثبات شد که ذر زوایای کوچک‌تر از ۱۵ درجه نیروی مقاوم متناسب با جابجایی است پس حرکت آونگ ساده یک حرکت نوسانی هماهنگ ساده است. با استفاده از رابطه جدید ضریب ثابت $$k$$، می‌توانیم دوره تناوب را برای آونگ ساده به شکل زیر بدست آوریم:

$$T = 2pi sqrt{dfrac{m}{k}} = 2pi sqrt{dfrac{m}{mg/L}}=2pi sqrt{dfrac{L}{g}}.$$

با توجه به رابطه فوق درمی‌یابیم که دوره تناوب در آونگ ساده فقط به طول آونگ و شتاب جاذبه بستگی دارد و به جرم جسم وابسته نیست.

مثال اول آونگ ساده

اگر یک آونگ ساده با طول ۷۵ سانتی‌متر و دوره تناوب ۱٫۷۳۵۷ ثانیه داشته باشیم شتاب گرانش زمین را حساب کنید.

پاسخ

با توجه با داده‌های سوال اگر زاویه حرکتی آونگ کمتر از ۱۵ درجه  باشد می‌توانیم از رابطه زیر استفاده کنیم.

$$T = 2pi sqrt{frac{L}{g}}$$

رابطه را برحسب g مرتب می‌کنیم.

$$g = 4pi^2 dfrac{L}{T^2}.$$

داده‌های سوال را در رابطه جایگذاری می‌کنیم.

$$g = 4pi^2 dfrac{0.75000 , m}{(1.7357 , s)^2}.$$

بنابراین شتاب گرانش به صورت زیر خواهد بود:

$$g = 9.8281 , m/s^2.$$

چگونه نوسان و موج را در فیزیک یاد بگیریم؟

برای فهم بهتر نوسان و موج در فیزیک، ابتدا باید با مفاهیم پایه‌ای آن‌ها آشنا شوید. نوسان به تکراری بودن حرکت یک سیستم حول موقعیت تعادلی خود اطلاق می‌شود، در حالی که موج، گسترش انرژی یا مواد در فضا است.

پس از درک مفاهیم ابتدایی، معادلات حاکم بر نوسان و موج را بررسی کنید. سپس، به تجزیه و تحلیل نوسان‌ها و موج‌ها به شکل‌های مختلف بپردازید.

در مرحله بعدی، مفاهیم پیشرفته‌تری را بررسی کنید که انتقال انرژی در موج، تنها بخشی از آن است. در نهایت، با استفاده از فیلم‌های آموزشی موجود در فرادرس، می‌توانید مفاهیم نوسان و موج در فیزیک را به طور کامل درک کرده و برای کاربردهای عملی آن‌ها آماده شوید.

می‌توانید فیلم‌های آموزشی مرتبط با نوسان و موج در فیزیک را از لینک‌های زیر در فرادرس مشاهده کنید:

همچنین فرادرس دروس متنوع و کاربردی را در زمینه فیزیک منتشر کرده است که اگر به این موضوع علاقه‌مند هستید می‌توانید آن‌ها را از طریق لینک زیر مشاهده کنید.

انرژی در نوسانگر هماهنگ ساده

در مبحث نوسان و موج، برای محاسبه انرژی نوسانگر هماهنگ ساده باید انواع انرژی‌هایی را که می‌تواند اختیار کند را بدانیم. از قانون هوک می‌دانیم که انرژی ذخیره شده در نوسانگر هماهنگ ساده برابر انرژی پتانسیل به صورت زیر است:

$$PR_{el} = dfrac{1}{2}kx^2.$$

از آنجا که در نوسانگر هماهنگ ساده اتلاف نیرو نداریم، شکل دیگری از انرژی که نوسانگر می‌تواند اختیار کند، انرژی جنبشی است که اگر با انرژی پتانسیل جمع کنیم به شکل زیر خواهد بود:

$$KE + PE_{el} =dfrac{1}{2}mv^2 + dfrac{1}{2}kx^2 = constant.$$

نکته: قانون بقای انرژی در نوسانگر هماهنگ ساده نیز صادق است.

برای آونگ ساده از تبدیلات زیر استفاده می‌کنیم:

$$v = Lomega$$

$$k = mg/L$$

$$x = Ltheta$$

رابطه بقای انرژی در نوسانگر هماهنگ ساده را با سه رابط فوق بازنویسی می‌کنیم:

$$dfrac{1}{2}mL^2omega^2 + dfrac{1}{2}mgLtheta^2 = constant.$$

اگر نوسانگر هماهنگ ساده نامیرا داشته باشیم، آنگاه انرژی بین شکل پتانسیل و جنبشی به طور دائم تبدیل می‌شود. مطابق شکل زیر اگر یک جسم روی سطح بدون اصطکاک باشد، حرکت با تمام انرژی ذخیره شده در فنر شروع می‌شود. وقتی جسم شروع به حرکت کرد، انرژی پتانسیل کم‌کم به انرژی جنبشی تبدیل می‌شود تا جایی که وقتی جسم در نقطه تعادل قرار داد فقط دارای انرژی جنبشی است. سپس دوباره به شکل انرژی پتانسیل تبدیل می‌شود. وقتی انرژی جنبشی کاملا به انرژی پتانسیل تبدیل می‌شود سرعت جسم صفر می‌شود.

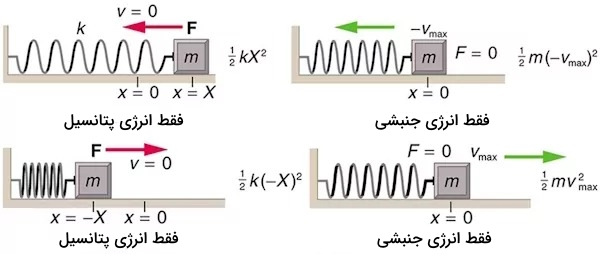
از قانون بقای انرژی می‌توان سرعت را برای نوسانگر هماهنگ ساده بدست آورد. اگر سرعت در نوسانگر هماهنگ ساده صفر باشد و بیشینه جابجایی $$x = X$$، آنگاه انرژی کل به صورت زیر خواهد بود:

$$dfrac{1}{2}kX^2.$$

این مقدار انرژی ثابت است و بین شکل جنبشی و پتانسیل تبدیل می‌شود.

$$dfrac{1}{2}mv^2 + dfrac{1}{2}kx^2 = dfrac{1}{2}kX^2.$$

معادله را برحسب $$v$$ مرتب می‌کنیم.

$$v = pm sqrt{dfrac{k}{m}(X^2 – x^2)}.$$

$$v = pmsqrt{dfrac{k}{m}}Xsqrt{1 – dfrac{x^2}{X^2}}$$

بنابراین سرعت به صورت زیر خواهد شد:

$$v = pm v_{max} sqrt{1 – dfrac{x^2}{X^2}}$$

در رابطه فوق بیشینه سرعت به شکل زیر است:

$$v_{max} = sqrt{dfrac{k}{m}}X.$$

همان‌طور که گفته شد بیشینه سرعت در $$x=0$$ رخ می‌دهند. در موضوع نوسان و موج، بیشینه سرعت به سه عامل دامنه، جرم جسم و ضریب ثابت $$k$$ بستگی دارد.

سرعت برای آونگ ساده به شکل زیر است:

$$omega_{max} = sqrt{dfrac{g}{L}}theta_{max}.$$

مثال اول بیشینه سرعت یک نوسانگر

بیشینه سرعت یک خودرو با وزن ۹۰۰ کیلوگرم که فنرهایی با ضریب ثابت $$k = 6.53 times 10^4 , N/m$$ دارد و به یک سرعت‌گیر برخورد کرده که باعث به وجود آمدن نوسان با دامنه ۰٫۱ متر در فنرها شده را محاسبه کنید.

پاسخ

با توجه به داده‌های سوال از رابطه بیشینه سرعت که در نوسان و موج گفته شد استفاده می‌کنیم.

$$v_{max} = sqrt{frac{k}{m}}X$$

داده‌ها را جایگذاری می‌کنیم.

$$v_{max} = sqrt{dfrac{6.53 times 10^4 , N/m}{900 , kg}}(0.100 , m).$$

در نتیجه بیشینه سرعت عمودی (بالا و پایین شدن خودرو) برابر مقدار زیر است:

$$v_{max} = 0.852 , m/s$$

مثال دوم بیشینه سرعت یک نوسانگر

دوره تناوب یک نوسانگر ۰٫۵ ثانیه و دامنه آن ۵ سانتی‌متر است، سرعت در نقطه تعادل را حساب کنید.

پاسخ

ابتدا سرعت زاویه‌ای را حساب می‌کنیم.

$$omega = frac{2pi}{T}= frac{2pi}{0.5} = 12.6 rad/sec$$

جون سرعت در نقطه تعادل خواسته شده بنابراین خواهیم داشت:

$$v=A omega = (5)(12.6) = 62.8 cm/sec$$

حرکت دایره‌ای یکنواخت

در مبحث نوسان و موج، یکی دیگر از نمونه‌های نوسان هماهنگ ساده، حرکت دایره‌ای یکنواخت است. مطابق شکل زیر یک توپ به یک دایره در حال چرخش متصل است و سایه آن روی زمین افتاده است. تغییرات سایه توپ را به عنوان نوسان هماهنگ ساده می‌توان در نظر گرفت. قانون هوک معمولا حرکت دایره‌ای یکنواخت (سرعت زاویه‌ای ثابت) را می‌تواند توصیف کند.

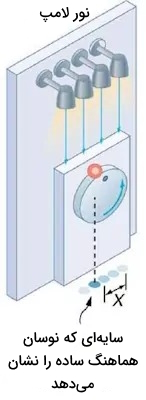
تصویر زیر رابطه ابتدایی بین حرکت دایره‌ای یکنواخت با نوسان هماهنگ ساده را نشان می‌دهد. نقطه ‌$$P$$ دایره را با سرعت زاویه‌ای ثابت می‌پیماید. مکان نقطه‌ $$P$$ روی محور مختصات مانند سایه توپ روی زمین در شکل قبل است. همان‌طور که در شکل نشان داده شده است مکان نقطه $$P$$ روی محور مختصات x هست و با سرعت $$v$$ به سمت چپ حرکت می‌کند. سرعت نقطه $$P$$ روی دایره برابر $$bar{v}_{max}$$ است.

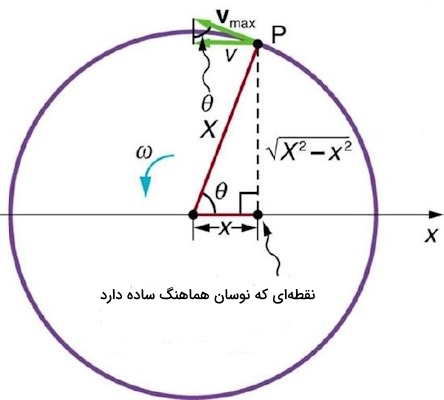
مکان $$x$$ در مسیر دایره‌ای به صورت زیر تعریف می‌شود:

‌$$x = X cos{theta}$$

با توجه به $$omega$$ سرعت زاویه‌ای و $$X$$ دامنه حرکت رابطه قوق را بازنویسی می‌کنیم.

$$x = X cos{omega t}$$

و چون $$omega = 2pi/T$$، معادله مکان وابسته به زمان به شکل زیر می‌شود:

$$x(t) = cos{left(frac{2pi t}{T}right)}.$$

این همان معادله مکان نوسان هماهنگ ساده است که در قسمت قبل بدست آوردیم. مثلث درون دایره که اضلاع آن  $$x$$ و $$X$$ و $$sqrt{X^{2} – x^{2}}$$ هستند، یک مثلث قائم الزاویه است که اگر تناسب زیر را در آن انجام دهیم:

$$frac{v}{v_{max}} = frac{sqrt{X^{X} – x^{2}}}{X} = sqrt{1-frac{x^{2}}{X^{2}}}.$$

اگر برحسب $$v$$ معادله را مرتب کنیم:

$$v = v_{max}sqrt{1 – frac{x^2}{X^{2}}}.$$

این معادله سرعت که از حرکت دایره‌ای یکنواخت بدست آمد دقیقا همان معادله سرعتی است که در نوسانگر هماهنگ ساده و در قسمت بقای انرژی مشاهده شد. برای محاسبه دوره تناوب حرکت دایره‌ای یکنواخت، نقطه $$P$$ باید یکبار کامل محیط دایره را طی کند. بنابراین دوره تناوب به شکل زیر است:

$$T = frac{2pi X}{v_{max}}.$$

از قسمت بقای انرژی بیشینه سرعت برابر مقدار زیر است:

$$v_{max} = sqrt{frac{k}{m}}X.$$

معادله فوق را برحسب $$X/v_{max}$$ می‌نویسیم.

$$frac{X}{v_{max}} = sqrt{frac{m}{k}}.$$

معادله فوق را در معادله دوره تناوب جایگذاری می‌کنیم.

$$tT = 2pi sqrt{frac{m}{k}}.$$

دوره تناوب حرکت دایره‌ای یکنواخت هم همانند دوره تناوب نوسانگر هماهنگ ساده است که قبلا محاسبه کرده بودیم.

اگر نمودار مکان برحسب زمان حرکت دایره‌ای یکنواخت را مانند شکل زیر رسم کنیم، شکل موج‌گونه‌ای را مشاهده خواهیم کرد که در مورد نوسانگر هماهنگ ساده نیز مشترک است.

حرکت هماهنگ میرا

یک نمونه از حرکت نوسانی میرا، توقف تدریجی تارهای مرتعش گیتار است. اگرچه ما معمولا اصطکاک و سایر نیروهای ناپایستار را صرف نظر می‌کنیم اما حرکت میرا بسیار نادر است. در این قسمت به بررسی حرکت نوسانی میرا از جمله کندمیرا، فرامیرا و میرایی بحرانی می‌پردازیم.

در مبحث نوسان و موج، در نوسانگر هماهنگ ساده اگر میرایی خیلی کوچک باشد، دوره تناوب و فرکانس تقریبا برابر هستند. اما دامنه به صورت تدریجی کاهش پیدا می‌کند زیرا نیروی ناپایستار انرژی را از سیستم به صورت گرما خارج می‌کند که به آن اتلاف انرژی نیز گفته می‌شود و به شکل زیر نشان می‌دهند:

$$W_{nc} = Delta (KE + PE)$$

$$W_{nc}$$ برای نوسانگر هماهنگ میرا منفی است چون انرژی مکانیکی را از سیستم حذف می‌کند.

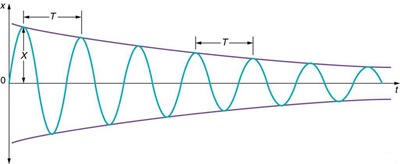
اگر به تدریج مقدار میرایی یک سیستم را افزایش دهید، دوره تناوب و فرکانس نیز دچار تغییر می‌شوند چون میرایی باعث کند شدن حرکت رفت و برگشتی می‌شود. (نیروی خالص در هر دو مسیر کوچکتر می‌شود). اگر میرایی خیلی زیاد باشد به طور کل مانع نوسان سیستم می‌شود و سیستم به آرامی به حالت پایدار خود برمی‌گردد.

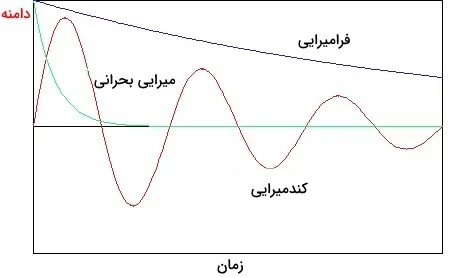
شکل زیر نمودار جابجایی نوسانگر هماهنگ در مقادیر مختلف میرایی را نشان می‌دهد. اگر بخواهیم نوسان یک سیستم را خیلی سریع کاهش دهیم، مانند تعلیق خودرو، در نتیجه سیستم به سرعت به حالت پایدار خود برسد. میرایی بحرانی به حالتی گویند که سیستم و یک نوسانگر با بیشترین سرعت ممکن به وضعیت تعادل خود برگردد. در میرایی بحرانی، سیستم ممکن است که از حالت تعادل خود خارج شود که این اتفاق فقط یکبار ممکن است رخ دهد.

حالت دیگر کندمیرا نام دارد که سیستم آهسته‌تر به وضعیت تعادل خود برمی‌گردد و دامنه نوسان به تدریج صفر می‌شود اما چندین بار سیستم از نقطه تعادل خود عبور می‌کند و حالت سوم فرامیرایی نام دارد که سیستم به صورت نمایی و بدون نوسان طی مدت طولانی‌تری به وضعیت تعادل خود برمی‌گردد.

نوسان واداشته و رزونانس

در این قسمت به بررسی مختصر «نیروی محرکه متناوب» (Periodic Driving Force) اعمال شده بر نوسانگر هماهنگ ساده می‌پردازیم. نیروی محرکه یک انرژی در فرکانس خاصی را به سیستم وارد می‌کند که لزوما فرکانس طبیعی سیستم نیست. فرکانس طبیعی سیستم، فرکانسی است که در آن سیستم بدون هیچ نیروی محرکه و میرایی نوسان می‌کند.

به زبان ساده اگر نیروی با فرکانس طبیعی به یک سیستم وارد شود، آن سیستم شروع به رزونانس یا «تشدید» (Resonance) می‌کند. در مبحث نوسان و موج، اگر فرکانس وارد شده به سیستم به طور قابل توجهی از مقدار فرکانس طبیعی آن افزایش یابد، آنگاه دامنه نوسان سیستم نیز کوچکتر می‌شود تا زمانی که نوسان کاملا متوقف شود.

شکل زیر نمودار دامنه برحسب فرکانس نیروی محرکه نوسانگر میرا است. سه منحنی در این نمودار وجود دارد که هر کدام نمایانگر مقدار متفاوتی از میرایی است. قله هر سه منحنی در جایی قرار دارد که فرکانس نیروی محرکه برابر فرکانس طبیعی نوسانگر هماهنگ است. بلندترین قله نشان دهنده کمترین مقدار میرایی است زیرا مقدار کمتری انرژی به واسطه نیروی میرایی از سیستم خارج شده است.

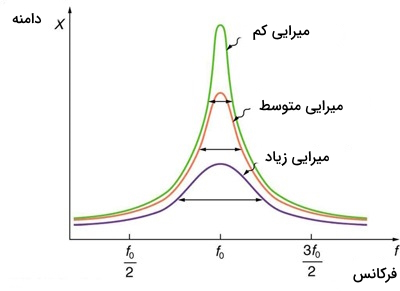
در شکل فوق هرچقدر میرایی کمتر باشد پهنای نمودار نیز کمتر می‌شود در نتیجه اگر شما بخواهید یک نواسانگر در یک فرکانس بخصوص تشدید کند، به حداقل میرایی نیاز خواهید داشت و اگر بخواهید دامنه نوسانگر کوچک باشد آنگاه به میرایی بیشتری نیاز دارید اما در این حالت سیستم با فرکانس‌های بیشتری پاسخ می‌دهد. یک مثال کاربردی از موضوع رزونانس می‌توان به دستگاه ام ار ای یا «تصویربرداری پرتو مغناطیسی» (Magnetic Resonance Imaging) اشاره کرد که هسته‌های اتمی به وسیله فرستادن امواج رادیویی (در حدود ۱۰۰ مگاهرتز) تشدید می‌کنند و بسیار در حوزه تشخیص پزشکی کاربرد دارد.

امواج

در این قسمت با ویژگی‌های امواج مکانیکی و نحوه محاسبه سرعت موج در حال انتشار آشنا خواهید شد. به بیان ساده موج اختلالی است که از جایی که ایجاد شده منتقل می‌شود. ساده‌ترین امواج خود را در چند دوره تکرار می‌کنند که با حرکت هماهنگ ساده همراه است.

در مجموع دو نوع موج داریم:

• موج مکانیکی
• موج الکترومغناطیسی

که در این مطلب فقط امواج مکانیکی را بررسی خواهیم کرد. ساده‌ترین مثال برای امواج مکانیکی، امواج دریا است. زمان یکبار حرکت بالا و پایین رفتن موج را دوره تناوب آن می‌گویند که با $$T$$ نمایش می‌دهند. فرکانس موج نیز عکس دوره تناوب هست:

$$f = 1/T$$

فاصله‌ای که موج در زمان معین طی می‌کند را سرعت انتشار یا سرعت موج می‌گویند.

$$v_w = dfrac{lambda}{T} = flambda. label{eq2}$$

در مبحث نوسان و موج، امواج دارای یک مشخصه دیگر به نام طول موج هستند که معمولا با $$lambda$$ نمایش می‌دهند که عبارت است از فاصله بین دو قله یا دو دره متوالی از یکدیگر که در شکل زیر مشاهده می‌کنید.

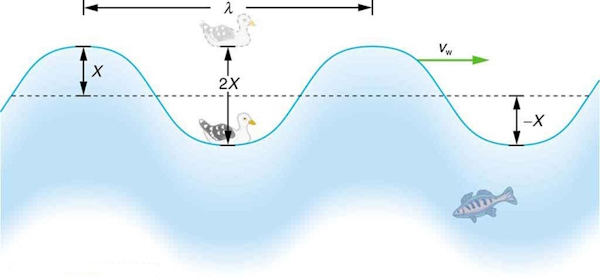
امواج مکانیکی به دو دسته تقسیم می‌شوند:

• موج طولی
• موج عرضی

امواج طولی: مطابق شکل زیر، به امواجی گفته می‌شود که جهت ارتعاش موازی با جهت انتشار است. مانند امواج صوتی در هوا.

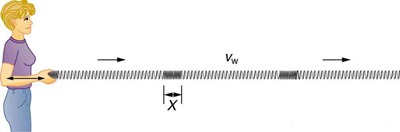
امواج عرضی: مطابق شکل زیر، به امواجی گفته می‌شود که جهت ارتعاش عمود بر جهت انتشار است. مانند یک سیم مرتعش گیتار.

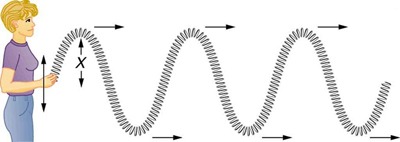
نکته: امواج ممکن است که ترکیبی از هردو موج طولی و عرضی باشند مانند موج دریا، امواج صوتی در محیط و زمین لرزه.

برهم‌نهی و اختلال

در این قسمت بیشتر با نوسان و امواج آشنا خواهیم شد و پدیده‌هایی مثل ضرب، امواج ایستاده، برهم‌نهی و اختلال را بررسی خواهیم کرد.

بسیاری از امواج شکل ساده‌ای ندارند. امواج ساده ممکن است به وسیله یک نوسانگر هماهنگ ساده به وجود آمده باشند در نتیجه شکل سینوسی خواهند داشت. امواج پیچیده، ترکیبی از امواج ساده‌تر هستند که در ادامه این مطلب به آن‌ها می‌پردازیم.

وقتی دو یا چند موج در یک نقطه به هم می‌رسند به نوعی با هم ادغام می‌شوند که به اصطلاح برهم‌نهی امواج گویند.

دسته‌بندی برهم‌نهی امواج

برهم‌نهی امواج را می‌توان به دو دسته سازنده و ویرانگر تقسیم کرد که در ادامه توضیح داده شده است.

برهم‌نهی سازنده

اگر دو یا چند موج زمانی که به هم می‌رسند هم‌فاز باشند یعنی اختلاف فاز صفر یا ۳۶۰ درجه داشته باشند، مطابق شکل زیر قله‌ها و دره‌های امواج در یک امتداد باشند، آنگاه دامنه موج تولید شده جدید برابر جمع دامنه امواج اولیه خواهد بود اما طول موج آن ثابت باقی می‌ماند.

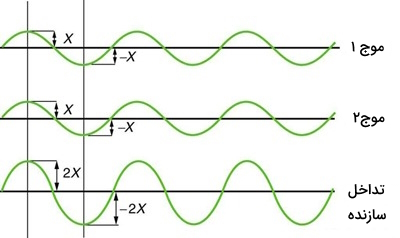
برهم‌نهی ویرانگر

اگر دو یا چند موج زمانی که به هم می‌رسند اختلاف فاز ۱۸۰ درجه باشد، مطابق شکل زیر قله‌ها و دره‌های امواج در یک امتداد نباشند، باعث می‌شود که دامنه موج تولید شده جدید صفر باشد، یعنی اصولا امواج یکدیگر را خنثی می‌کنند.

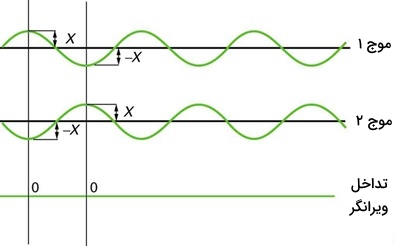
اگرچه برهم‌نهی سازنده و ویرانگر اتفاق می‌افتد اما نیازمند آن است که اختلاف فاز دقیقا معادل مقادیر گفته شده باشد. برهم‌نهی امواج ممکن است ترکیبی از برهم‌نهی سازنده و ویرانگر همزمان باشد. برای مثال صدای خروجی از یک بلندگو استریو ممکن است که در یک نقطه زیاد و در نقطه‌ای دیگر کم باشد. این تغییر صدا به این معنی است که امواج صوتی در مکان‌هایی تداخل سازنده دارند و در مکان‌هایی تداخل ویرانگر دارند. مثال دیگر صدای خروجی از موتورهای جت هواپیما طی زمان است که توسط مسافر شنیده می‌شود. صدای تولید شده توسط دو موتور هواپیما طی زمان می‌تواند زیاد یا کم باشد که نشان دهنده‌ی سازنده یا ویرانگر بودن امواج در طول زمان است.

گاهی اوقات به نظر می‌رسد که امواج حرکت نمی‌کنند و فقط در یک نقطه ارتعاش می‌کنند. مطابق شکل زیر وقتی دو موج خلاف جهت یکدیگر حرکت می‌کنند، اگر دامنه و طول موج یکسان داشته باشند، آنگاه اختلال موج جدید مدام بین حالت سازنده و ویرانگر تغییر می‌کند. این حالت خاص به نظر شبیه به یک موج ایستاده است که به اصطلاح به این نوع امواج، ایستاده گویند.

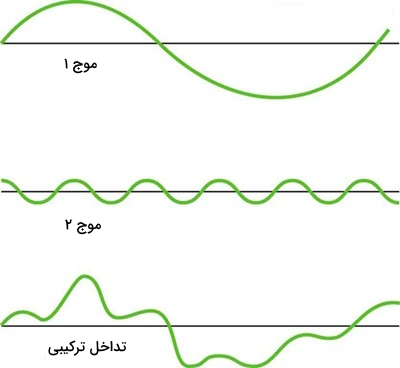
زمین لرزه یک مثال خوب برای امواج ایستاده، رزونانس، تداخل سازنده و ویرانگر است. در هنگام زمین لرزه یک ساختمان ممکن است که برای چند ثانیه بلرزد اما آسیبی به آن وارد نشود در حالی که ساختمان کناری آن کاملا ویران شود. علت این پدیده این است که فرکانس زمین لرزه با فرکانس طبیعی ساختمان اول هم‌فاز بوده بنابراین اختلال سازنده داشته است درحالی‌که در ساختمان کناری فرکانس زمین لرزه با فرکانس طبیعی آن اختلاف فاز داشته در نتیجه اختلال ویرانگر داشته است.

امواج ایستاده در سازهای زهی نیز تولید می‌شوند. مطابق شکل زیر تارهایی که دو سر آن‌ها بسته هستند نشان داده شده است. در مبحث نوسان و موج، به نقطه‌ای که تار در آنجا حرکت نمی‌کند «گره» (Node) می‌گویند. به طور ساده‌تر نقاطی که اختلال در موج ایستاده برابر صفر است گره وجود دارد. دو سر تار که بسته است جز نقاط گره محسوب می‌شود. به نقاطی که دامنه در امواج ایستاده بیشینه است پادگره یا شکم یا «حلقه» (Loop) می‌گویند.

امواج ایستاده در تار، فرکانس با سرعت انتشار $$v_w$$ ارتباط دارد. فاصله بین دو نقطه ثابت از تار را طول موج تار می‌گویند.

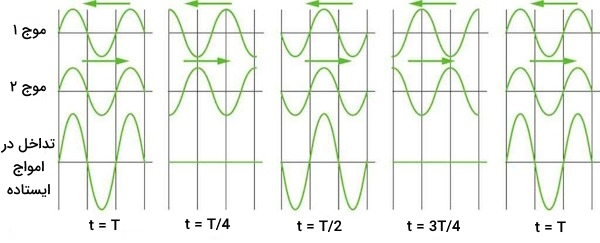
کمترین مقدار فرکانس را به اصطلاح فرکانس بنیادی یا اولیه گویند که طولانی‌ترین طول موج را نیز دارد به شکل زیر است.

$$lambda_1 = 2L$$

بنابراین فرکانس بنیادی به صورت زیر خواهد بود:

$$f_1 = v_w/lambda_1 = v_w/2L$$

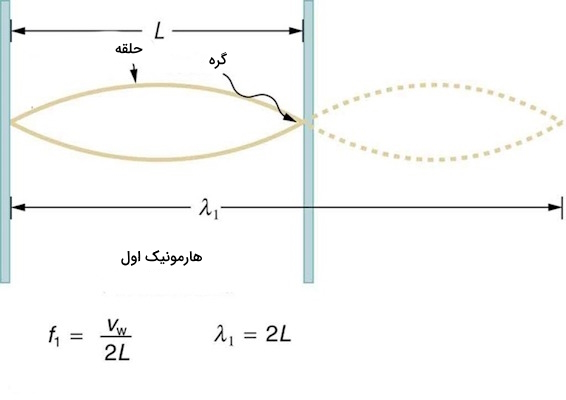
هارمونیک‌های دیگر به صورت یک ضریب از فرکانس بنیادی تار هستند. همان‌طور که در شکل زیر مشاهده می‌کنید هارمونیک اول و دوم به صورت زیر محاسبه می‌شود:

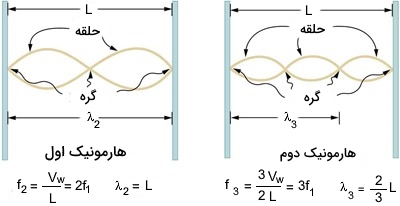
$$lambda_2 = LRightarrow f_2 = v_w/lambda_2 = v_w/2L = 2f_1$$

$$f_3 = 3f_1$$

تمام این فرکانس‌ها با تغییر تنش در تار قابل تغییر هستند. تنش بیشتر باعث افزایش سرعت انتشار و فرکانش می‌شود.

ضرب

وقتی دو موج بسیار شبیه به هم با یکدیگر اختلال کنند اما فقط فرکانس آن‌ها کمی متفاوت باشد پدیده «ضرب» (Beat) رخ می‌دهد. برای مثال وقتی همزمان دو کلید مجاور پیانو را فشار می‌دهید چون دو موج تولید بسیار به هم نزدیک هستند و برهم‌نهی سازنده و ویرانگر یکی پس از دیگری تکرار می‌شود در این صورت ضرب رخ می‌دهد.

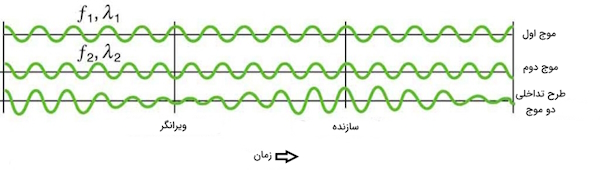
در مبحث نوسان و موج، فرکانس موج حاصل از برهم‌نهی دو موج با فرکانس شبیه به هم در واقع میانگین فرکانس آن‌ها است. این موج با فرکانسی نوسان می‌کند که به آن فرکانس ضرب گویند که می‌توان با جمع جبری امواج تولید کننده آن را محاسبه کرد. یک موج را می‌توان به صورت یک نقطه در فضا تعریف کرد:

$$x = X , cos left(dfrac{2pi t}{T} right) = X , cos , (2pi , ft)$$

در رابطه فوق $$f = 1/T$$ فرکانس موج است. جمع دو موج که دامنه یکسان ولی فرکانس متفاوت دارند به صورت زیر است:

$$x = x_1 + x_2.$$

$$x = X , cos (2pi , f_1 t) + X , cos (2pi , f_2 t).$$

$$x = 2X , cos (pi , f_Bt) cos (2pi , f_{ave}t),$$

فرکانس ضرب به صورت زیر است:

$$f_B = |f_1 – f_2|$$

انرژی در امواج

در این قسمت به بررسی شدت و توان در امواج می‌پردازیم. تمام امواج حامل انرژی هستند مانند امواج زلزله که می‌تواند یک شهر را تخریب کند. مقدار انرژی موج به دامنه آن بستگی دارد برای مثال زلزله با دامنه بزرگ، جابجایی بزرگی نیز ایجاد می‌کند. جابجایی $$X$$ رابطه مستقیمی با نیرو $$F = kx$$ دارد همچنین از طریق رابطه کار و انرژی می‌توان دامنه را به انرژی ربط داد:

$$W propto F_x = kx^2.$$

انرژی در امواج به زمان نیز بستگی دارد به عنوان مثال هرچقدر یک دستگاه گرمایش فراصوت روشن باشد، انرژی بیشتری منتقل می‌کند. در مبحث نوسان و موج، امواج می‌توانند متمرکز یا پراکنده شوند. این موضوعات در تفسیر شدت در امواج به کار می‌روند. شدت به صورت توان بر واحد سطح تعریف می‌شود.

$$I = frac{P}{A}$$

تعریف شدت برای هر نوع انتقال انرژی معتبر است که شامل امواج نیز می‌شود. واحد شدت در سیستم Si، وات بر مجذور متر $$(W/m^2)$$ است.

مثال اول انرژی در امواج

میانگین شدت نور خورشید بر سطح زمین تقریبا $$700 , W/m^2$$ است.

الف: مقدار انرژی جذب شده توسط یک پنل خورشید با مساحت ۰٫۵ مترمربع به مدت ۴ ساعت را حساب کنید.

ب: اگر به وسیله یک ذره‌بین نور تابیده به سطح را تا ۲۰۰ برابر کوچکتر کنیم، شدت نور در آن نقطه چقدر خواهد شد؟

پاسخ

برای حل قسمت (الف) از روابط زیر باید استفاده کنیم:

$$I = dfrac{P}{A}. nonumber$$

$$I = dfrac{E/t}{A}. nonumber$$

در نتیجه رابطه انرژی به صورت زیر خواهد بود:

$$E = IAt. nonumber$$

با جایگذاری داده‌های سوال در رابطه فوق خواهیم داشت:

$$E = (700 , W/m^2)(0.500 , m^2)[(4.00 , h)(3600 , s/h)] = 5.04 times 10^6 , J. nonumber $$

برای حل قسمت (ب)، نسبت شدت جدید که با پریم مشخص می‌کنیم به شدت قدیم محاسبه می‌کنیم:

$$dfrac{I’}{I} = dfrac{P’A’}{P/A} = dfrac{A}{A’} nonumber$$

توان‌های جدید و قدیم در تناسب خنثی می‌شوند.

$$P’ = P$$

در نتیجه خواهیم داشت:

$$A = 200 A,$$

$$dfrac{I’}{I} = 200. nonumber$$

با جایگذاری داده‌های سوال در رابطه فوق خواهیم داشت:

$$I’ = 200 I = 200(700 , W/m^2). nonumber$$

$$I’ = 1.40 times 10^5 , W/m^2. nonumber$$

بنابراین با کاهش مساحت، شدت افزایش قابل توجهی پیدا می‌کند.

مثال دوم انرژی در امواج

دو موج یکسان که هر کدام دارای شدت $$1.00 , W/m^2$$ هستند تداخل سازنده دارند، شدت موج جدید را حساب کنید.

پاسخ

از نوسان و موج می‌دانیم دو موج یکسان که دامنه برابر دارند وقتی تداخل سازنده با یکدیگر دارند دامنه موج جدید دو برابر خواهد شد. چون شدت موج با مربع دامنه متناسب است در نتیجه شدت موج جدید ۴ برابر موج اولیه خواهد بود.

$$I’ propto (X’)^2 = (2X)^2 = 4X^2.$$

$$I propto X^2.$$

$$dfrac{I’}{I} = 4.$$

با جایگذاری داده‌های سوال در رابطه فوق خواهیم داشت:

$$I’ = 4I = 4.00 , W/m^2.$$

مثال سوم انرژی در امواج

دیافراگم یک بلندگو دارای وزن ۵۰ گرم و فرکانس ۲ کیلوهرتز و دامنه $$1.8times 10^{-4}m$$ است.

الف: بیشینه نیروی وارده بر بلندگو را حساب کنید.

ب: انرژی مکانیکی دیاگرام را محاسبه کنید.

پاسخ

برای حل قسمت (الف) به شیوه زیر نیروها را جمع می‌کنیم:

$$sum F = F_{text{max}} = ma_{text{max}} = m(A omega^2) = m(A(2 pi f)^2) = 4 pi^2 mf^2 A^2=1400N$$

برای حل قسمت (الف) چون انرژی مکانیکی پایستار است بنابراین خواهیم داشت:

$$E = K_{text{max}} = U_{text{max}}$$

$$K_{text{max}} = -frac{1}{2}mv_{text{max}}^2 = -frac{1}{2}m(Aomega)^2 = -frac{1}{2}mA^2(2pi f)^2=0.13J$$

نتیجه‌گیری

نوسان و موج نقش مهمی در زندگی ما دارند و همین‌طور جز موضوعات مهم در فیزیک است. در این مطلب از مجله فرادرس به معرفی امواج و انواع نوسانگرها و مشخصات آن‌ها از جمله طول موج، فرکانس، نیرو و انرژی پرداخته شد و چند مثال برای درک بهتر این موضوع ارائه شد.