یادگیری ماشین به سه روش عمده «یادگیری نظارت شده» (Supervised Learning)، «یادگیری نظارت نشده» (Unsupervised Learning) و «یادگیری نیمه نظارت شده» (Semi-Supervised Learning) تقسیم می‌شود که استفاده از هر کدام به نوع داده‌های مسئله بستگی دارد. در یادگیری نظارت نشده مجموعه‌دادها بدون برچسب هستند؛ به این معنی که اطلاعتی درباره الگوهای پنهان موجود در داده‌ها نداریم و باید پیدا کردن آن‌ها را به الگوریتم‌های مرتبط بسپاریم. الگوریتم های خوشه بندی از جمله روش‌هایی هستند که در مسائل مرتبط با یادگیری نظارت نشده به کار می‌روند. همچنین در علوم داده از تحلیل خوشه‌بندی برای آشنایی با داده‌های گروه‌بندی شده به‌وسیله الگوریتم خوشه‌بندی استفاده می‌شود. در این مطلب از مجله فرادرس، با ۱۰ مورد از کاربردی‌ترین الگوریتم های خوشه بندی در یادگیری ماشین آشنا شده و نحوه پیاده‌سازی هر کدام را یاد می‌گیریم.

در این مطلب، ابتدا تعریفی از خوشه‌بندی ارائه داده و به شرح چهار دسته کلی از الگوریتم های خوشه بندی می‌پردازیم. سپس با موارد استفاده این الگوریتم ها آشنا شده و ۱۰ مورد از رایج‌ترین آن‌ها را معرفی و پیاده‌سازی می‌کنیم. در انتهای این مطلب از مجله فرادرس، چند مورد از کاربردهای خوشه‌بندی را بررسی کرده و به سوالات متداول در این زمینه پاسخ می‌دهیم.

خوشه ‌بندی چیست؟

روش «خوشه‌بندی» (Clustering) زیرمجموعه‌ای از یادگیری نظارت نشده است که به دلیل نحوه کارکرد آن، «تحلیل خوشه» (Cluster Analysis) نیز نامیده می‌شود. با بهره‌گیری از الگوریتم خوشه بندی، داده‌های بدون برچسب زیادی در اختیار آن قرار داده و اجازه می‌دهیم تا نمونه‌ها را در گروه‌های مجزا طبقه‌بندی کند. به هر یک از این گروه‌ها «خوشه» می‌گویند. یک خوشه، گروهی شامل نقاط داده شبیه به یک‌دیگر از نظر ارتباط‌شان با نمونه‌های مجاور است. خوشه‌بندی در رویکردهایی همچون «مهندسی ویژگی» (Feature Engineering) و «کشف الگو» (Pattern Discovery) کاربرد دارد. در ابتدای کار، اطلاعات چندانی درباره مسئله نداریم و به همین خاطر، بهره‌گیری از الگوریتم های خوشه بندی نقطه شروع خوبی برای آشنایی با داده‌ها است.

دسته بندی الگوریتم های خوشه بندی

الگوریتم های خوشه بندی برای مدیریت انواع داده، از روش‌های مختلفی تشکیل شده‌اند که در این بخش به بررسی چهار گروه اصلی آن می‌پردازیم.

روش های مبتنی بر چگالی

در الگوریتم های خوشه بندی «مبتنی‌بر چگالی» (Density-based)، داده‌ها بر اساس نواحی با تراکم و چگالی کمتر، در خوشه‌هایی متراکم و با چگالی بیشتر دسته‌بندی می‌شوند. به بیان ساده‌تر، این الگوریتم‌ها نواحی متراکم را پیدا کرده و هر کدام را یک خوشه می‌نامند. در روش‌های مبتنی‌بر چگالی، شکل خوشه‌ها قاعده مشخصی نداشته و همچنین شرایط محدود کننده‌ای نیز برای الگوریتم وجود ندارد. باید به این نکته توجه داشت که در این دسته از روش‌ها، تلاشی برای دسته‌بندی «نمونه‌ها پَرت» (Outliers) صورت نمی‌گیرد و چنین نمونه‌هایی تنها نادیده گرفته می‌شوند.

روش های مبتنی‌ بر توزیع

استفاده از الگوریتم های خوشه بندی «مبتنی‌بر توزیع» (Distribution-based) تضمین می‌کند، تمامی نقاط داده بر اساس درصدی از احتمال در خوشه‌ای خاص قرار می‌گیرند. همزمان با افزایش فاصله یک نمونه با مرکز خوشه، احتمال قرار گرفتن آن نمونه در خوشه کاهش پیدا می‌کند. استفاده از روش‌های مبتنی‌بر توزیع، تنها زمانی پیشنهاد می‌شود که توزیع داده‌ها مشخص باشد.

روش های مبتنی‌ بر مرکز

شاید بتوان از روش‌های مبتنی‌بر مرکز به عنوان رایج‌ترین الگوریتم های خوشه بندی یاد کرد. این دسته از الگوریتم‌ها کمی به پارامترهای اولیه حساس بوده اما به‌طور کلی روش‌های سریع و موثری به حساب می‌آیند. در این نوع از الگوریتم‌ها، تقسیم نقاط داده بر اساس چندین مرکز خوشه انجام می‌شود. به این صورت که هر نمونه بر اساس مربع فاصله‌اش تا مرکز، به خوشه مربوطه تخصیص پیدا می‌کند.

روش های سلسله مراتبی

عمده استفاده از الگوریتم های خوشه بندی «سلسله مراتبی» (Hierarchical-based) برای داده‌های به اصطلاح سلسله مراتبی مانند «پایگاه داده» (Database) است. در این روش‌ها به‌منظور سامان‌دهی بیشتر، خوشه‌ها به شکل درختی از بالا به پایین مرتب می‌شوند. با وجود این‌که الگوریتم های خوشه بندی سلسله مراتبی، نسبت به سایر روش‌ها محدودیت بیشتری دارند، برای مجموعه‌داده‌های ترتیبی عملکرد بسیار خوبی از خود به نمایش می‌گذارند.

چه زمان از الگوریتم های خوشه بندی استفاده کنیم؟

اگر مجموعه‌داده شما فاقد نمونه‌های برچسب‌گذاری شده باشد، به احتمال زیاد باید از نوعی الگوریتم نظارت نشده استفاده کنید. از جمله تکنیک‌های یادگیری نظارت نشده می‌توان به «شبکه‌های عصبی» (Neural Networks)، «یادگیری تقویتی» (Reinforcement Learning) و خوشه‌بندی اشاره کرد. نوع الگوریتم مناسب هر مسئله، به شکل مرتب شدن داده‌ها بستگی دارد.  به عنوان مثال در «تشخیص ناهنجاری» (Anomaly Detection)، الگوریتم های خوشه بندی با گروه‌بندی نقاط داده در خوشه‌های مجزا، مرز میان نمونه‌های عادی و پرت را مشخص می‌کنند.

اگر در انتخاب ویژگی برای مدل یادگیری ماشین خود تردید دارید، الگوریتم های خوشه بندی با کشف الگوهای پنهان به شما در یافتن ویژگی‌های مناسب کمک می‌کنند. به‌طور کلی، هر چه اطلاعات محدودتری نسبت به داده‌ها داشته باشید، یعنی خوشه‌بندی همان روشی است که باید در نظر بگیرید. شاید انتخاب الگوریتم خوشه بندی مناسب کمی زمان‌بر باشد، اما در مرحله بعدی متوجه روابطی ارزشمند میان داده‌ها می‌شوید.

تشخیص کلاهبرداری در امور بیمه، دسته‌بندی کتاب‌های یک کتابخانه و بخش‌بندی مشتریان، تنها چند نمونه از کاربردهای بسیار الگوریتم های خوشه بندی است. علاوه‌بر آن، الگوریتم های خوشه بندی در کاربردهایی با مقایس بزرگ‌تر مانند «تحلیل زلزله» (Earthquake Analysis) یا «برنامه‌ریزی شهری» (City Planning) نیز کاربرد دارند.

انواع الگوریتم های خوشه بندی

پس از آشنایی با نحوه کارکرد الگوریتم های خوشه بندی، در این بخش با بهره‌گیری از کتابخانه scikit-learn در زبان برنامه‌نویسی پایتون، به معرفی و پیاده‌سازی ۱۰ مورد کاربردی از این الگوریتم‌ها می‌پردازیم. شما می‌توانید هر کدام از مثال‌های مطرح شده در ادامه این مطلب از مجله فرادرس را برای تمرین‌های پایتون شخصی‌سازی و استفاده کنید.

نصب کتابخانه مورد نیاز

ابتدا باید کتابخانه scikit-learn را نصب کنیم. مانند تمامی کتابخانه‌ها در زبان برنامه‌نویسی پایتون، این کتابخانه نیز از طریق ابزار pip و با دستور زیر قابل نصب است:

sudo pip install scikit-learn

برای کسب اطلاعات بیشتر در مورد آموزش نصب کتابخانه scikit-learn، می‌توانید به صفحه رسمی «+» آن مراجعه کنید. پس از نصب کتابخانه، با اجرای قطعه کد زیر، از به‌روز بودن نسخه scikit-learn اطمینان حاصل می‌کنیم:

1# check scikit-learn version
2import sklearn
3print(sklearn.__version__)

پس از اجرای قطعه کد بالا، شماره آخرین نسخه کتابخانه به شما نمایش داده می‌شود:

1.3.0

مجموعه داده مورد استفاده در مثال ها

در مرحله بعد از تابع make_classfication

  استفاده و مجموعه‌داده‌ای آزمایشی ایجاد می‌کنیم. این مجموعه‌داده متشکل از ۱۰۰۰ نمونه با ۲ ورودی و یک خوشه به‌ازای هر کلاس است. خوشه‌ها در فضایی دو بعدی و نقاط داده با «نمودار نقطه‌ای» (Scatter Plot) و رنگ‌های متفاوت برای هر خوشه به نمایش گذاشته می‌شوند. قابل ذکر است که توزیع خوشه‌های این مسئله آموزشی، از نوع «گاوسی چند متغیره» (Multivariate Gaussian) بوده که شناسایی موثر آن برای تمامی الگوریتم های خوشه بندی میسر نیست. به همین خاطر، نتایج به‌دست آمده نباید مبنایی برای مقایسه عمومی روش‌ها قرار گیرند.

با استفاده از تابع make_classfication

، می‌توانید مجموعه‌داده‌ای مناسب مسائل خوشه‌بندی ساخته و نمونه‌ها را در فضایی دو بعدی ترسیم کنید:

1# synthetic classification dataset
2from numpy import where
3from sklearn.datasets import make_classification
4from matplotlib import pyplot
5
6# define dataset
7X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
8# create scatter plot for samples from each class
9for class_value in range(2):
10	# get row indexes for samples with this class
11	row_ix = where(y == class_value)
12	# create scatter of these samples
13	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
14# show the plot
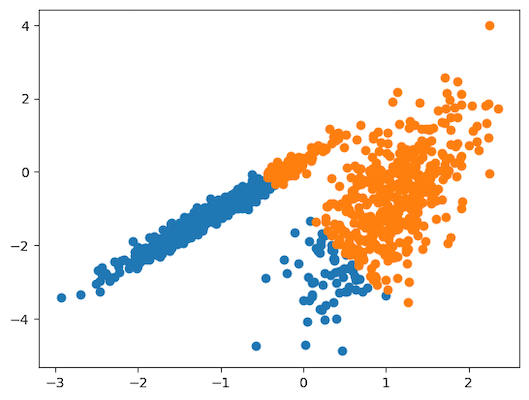
15pyplot.show()

با اجرای قطعه کد بالا، مجموعه‌داده‌ای مصنوعی تولید شده و نموداری نقطه‌ای از داده‌های ورودی با دو رنگ مختلف ترسیم می‌شود:

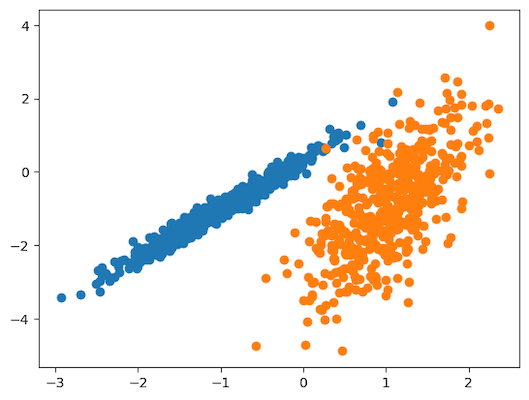
همان‌طور که در تصویر نیز ملاحظه می‌کنید، نقاط داده در دو گروه متمایز قرار داشته و باید ببینیم که آیا الگوریتم های خوشه بندی قادر به شناسایی این دو گروه هستند یا خیر. در ادامه، از این مجموعه‌داده برای سنجش عملکرد الگوریتم های خوشه بندی استفاده می‌کنیم.

۱. الگوریتم خوشه بندی K میانگین

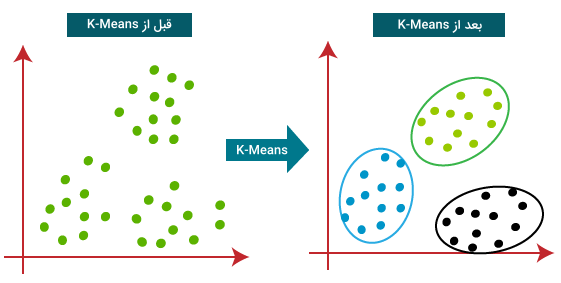
شاید بتوان از «خوشه‌بندی K میانگین» (K-Means) به عنوان شناخته شده‌ترین الگوریتم خوشه‌بندی یاد کرد. الگوریتمی که به‌طور معمول در کلاس‌های آموزشی علوم داده و یادگیری ماشین تدریس می‌شود. درک و پیاده‌سازی خوشه‌بندی K میانگین راحت بوده به چند مرحله تقسیم می‌شود:

1. در مرحله اول، تعدادی کلاس یا گروه انتخاب شده و نقاط مرکزی هر کدام به صورت تصادفی مقداردهی اولیه می‌شوند. برای آن‌که بتوانیم انتخاب بهتری در تعداد کلاس‌ها داشته باشیم، باید داده‌ها را بررسی کرده و به‌دنبال ویژگی‌های متمایز کننده میان آن‌ها بگردیم. نقاط مرکزی، بردارهایی هم‌اندازه سایر نقاط داده هستند و بر روی محور xها نگاشت می‌شوند.
2. با محاسبه فاصله میان هر نمونه و مراکز خوشه‌ها، نقاط داده در خوشه‌ای که به مرکز آن نزدیک‌تر هستند قرار می‌گیرند.
3. پس از اتمام دسته‌بندی نقاط داده، مجدد موقعیت مراکز خوشه، این بار با میانگین گرفتن از تمامی داده‌های موجود در آن گروه محاسبه می‌شوند.
4. این مراحل را تا زمانی تکرار می‌کنیم که حد آستانه‌ای مشخص رعایت شده و یا موقعیت مکانی مراکز خوشه تغییر چندانی نداشته باشند. همچنین می‌توان چند مرتبه نقاط مرکزی را به صورت تصادفی مقداردهی اولیه کرده و سپس بهترین نتیجه را انتخاب کرد.

از آنجا که تنها فاصله میان نقاط داده و مراکز خوشه محاسبه می‌شود، سرعت بالا از جمله مزیت‌های الگوریتم K میانگین به شمار می‌آید. با این حال، این الگوریتم معایبی نیز دارد. در اولین قدم باید خودمان تعداد گروه‌ها را مشخص کنیم. فرایندی که نه آسان است و نه ایده‌آل برای الگوریتمی که هدف آن در کمک به شناخت بهتر داده‌ها خلاصه می‌شود. همچنین مقداردهی اولیه موقعیت مراکز خوشه به‌صورت تصادفی است که امکان دارد در اجرای‌های متعدد به خوشه‌هایی متفاوت ختم شود. بدین ترتیب نتایج، غیرقابل تکرار و فاقد ثبات هستند.

پایداری و ثبات دیگر الگوریتم های خوشه بندی به مراتب از روش K میانگین بیشتر است. الگوریتم خوشه‌بندی «K میانه» (K-Median) شبیه به الگوریتم K میانگین است؛ با این تفاوت که برای محاسبه مجدد مراکز خوشه از معیار میانه بردارهای نمونه هر کلاس استفاده می‌کند. احتمال وجود نمونه‌های پرت در این الگوریتم کمتر بوده اما از طرفی و چون محاسبه بردار میانه به مرتب‌سازی نیاز دارد، عملکرد آن برای مجموعه‌داده‌های بزرگ به مراتب آهسته‌تر است.

پیاده‌سازی الگوریتم K میانگین از طریق کلاس KMeans

  انجام می‌شود و پارامتر ورودی n_clusters

  نیز تعداد تقریبی خوشه‌ها را مشخص می‌کند:

1# k-means clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.cluster import KMeans
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = KMeans(n_clusters=2)
12# fit the model
13model.fit(X)
14# assign a cluster to each example
15yhat = model.predict(X)
16# retrieve unique clusters
17clusters = unique(yhat)
18# create scatter plot for samples from each cluster
19for cluster in clusters:
20	# get row indexes for samples with this cluster
21	row_ix = where(yhat == cluster)
22	# create scatter of these samples
23	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
24# show the plot
25pyplot.show()

با اجرای قطعه کد بالا، مدلی بر مجموعه‌داده آموزشی برازش شده و خوشه‌ای برای هر نمونه در مجموعه‌داده پیش‌بینی می‌شود. سپس نموداری نقطه‌ای ایجاد و نقاط داده رنگی بر اساس خوشه‌ای که در آن قرار دارند ترسیم می‌شوند.

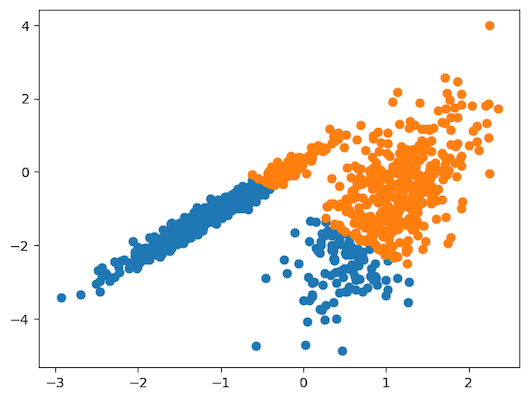
همان‌طور که در نمودار نیز مشاهده می‌کنید، گروه‌بندی به نسبت خوبی صورت گرفته است. اما «واریانس» (Variance) نابرابر نقاط داده در دو بعد، نشان‌دهنده انتخاب نه چندان مناسب الگوریتم K میانگین برای این مسئله است.

۲. الگوریتم خوشه بندی K میانگین با دسته های کوچک

الگوریتم «خوشه‌بندی K میانگین با دسته‌های کوچک» (Mini-Batch K-Means)، نسخه‌ای تغییر یافته از الگوریتم K-Means است که در هر تکرار، به‌جای میانگین‌گیری از تمامی نمونه‌های مجموعه‌داده، تنها میانگین دسته کوچکی از داده‌ها را محاسبه می‌کند. در نتیجه سرعت پردازش مجموعه‌داده‌های حجیم بالاتر رفته و نسبت به داده‌های نویزی نیز مقاوم‌تر می‌شود. در قطعه کد زیر، نمونه‌ای از پیاده‌سازی این الگوریتم را با استفاده از کلاس MiniBatchKMeans

  ملاحظه می‌کنید:

1# mini-batch k-means clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.cluster import MiniBatchKMeans
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = MiniBatchKMeans(n_clusters=2)
12# fit the model
13model.fit(X)
14# assign a cluster to each example
15yhat = model.predict(X)
16# retrieve unique clusters
17clusters = unique(yhat)
18# create scatter plot for samples from each cluster
19for cluster in clusters:
20	# get row indexes for samples with this cluster
21	row_ix = where(yhat == cluster)
22	# create scatter of these samples
23	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
24# show the plot
25pyplot.show()

مطابق انتظار، نتیجه این روش نیز مشابه الگوریتم K-Means و مانند نمودار زیر است:

۳. الگوریتم خوشه بندی تغییر میانگین

روش خوشه‌بندی «تغییر میانگین» (Mean Shift)، الگوریتمی مبتنی‌بر «جابه‌جایی پنجره» (Sliding-window-based) است و تلاش دارد تا نواحی متراکم نقاط داده را پیدا کند. الگوریتم تغییر میانگین از گروه الگوریتم‌های مبتنی‌بر مرکز است؛ به این معنی که ابتدا میانگین نقاط داده موجود در پنجره را محاسبه کرده و موقعیت مرکز خوشه را به آن مقدار به‌روزرسانی می‌کند. در انتها و طی مرحله‌ای، پنجره‌های مشابه حذف شده و مجموعه نهایی مراکز خوشه همراه با گروه‌های متناظر باقی می‌مانند. مراحل اجرای الگوریتم خوشه‌بندی تغییر میانگین به شرح زیر است:

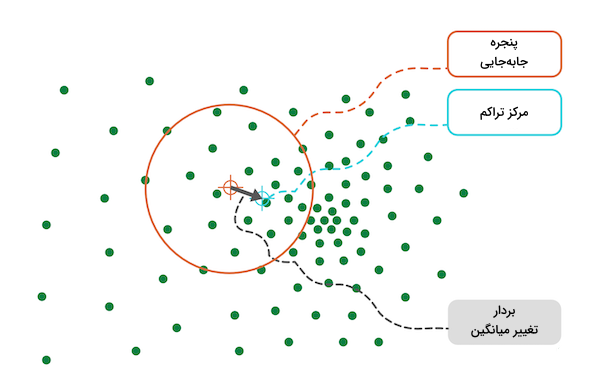
1. برای شرح این الگوریتم از فضایی دو بعدی مانند تصویر بالا استفاده می‌کنیم. با یک پنجره دایره‌ای شروع کرده و نقطه‌ای تصادفی مانند $$ C $$ را به عنوان مرکز و مقدار $$ r $$ که برابر با شعاع دایره است را به عنوان «کرنل» (Kernel) در نظر می‌گیریم. روش خوشه‌بندی تغییر میانگین، نوعی الگوریتم «تپه نوردی» (Hill-climbing) است که به‌طور مکرر، موقعیت کرنل را در هر مرحله و تا رسیدن به همگرایی تغییر می‌دهد.
2. در هر تکرار، موقعیت مرکز خوشه به میانگین نمونه‌های داخل پنجره تغییر یافته و پنجره به سمت ناحیه‌ای با چگالی بیشتر حرکت می‌کند. تراکم و چگالی هر پنجره متناسب با تعداد نمونه‌های درون آن است. به صورت طبیعی و با انتقال بر اساس میانگین نقاط داده، پنجره به سمت نواحی با چگالی بالاتر جابه‌جا می‌شود.
3. فرایند جابه‌جایی پنجره تا جایی ادامه پیدا می‌کند که تعداد نمونه‌ها در کرنل به حداکثر رسیده باشد. به بیان ساده‌تر، فرایند جابه‌جایی پنجره را تا پیدا کردن متراکم‌ترین ناحیه ادامه می‌دهیم.
4. مراحل ۱ تا ۳ با چند پنجره اجرا شده و پنجره‌ای که بیشترین تعداد نمونه را در خود جای دهد انتخاب و در نهایت، نقاط داده بر اساس پنجره‌ای که در آن قرار دارند، خوشه‌بندی می‌شوند.

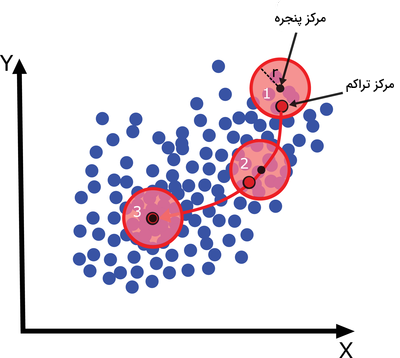
در این روش بر خلاف الگوریتم K میانگین، تعداد خوشه‌ها به‌صورت خودکار مشخص شده و نیازی به تعریف آن توسط ما نیست. یکی دیگر از مزایای این الگوریتم، همگرایی مراکز خوشه به سمت متراکم‌ترین نواحی است. انتخاب شعاع پنجره یا همان $$ r $$، ممکن است کمی دشوار باشد و از همین جهت، به عنوان یکی از معایب الگوریتم تغییر میانگین از آن یاد می‌شود. الگوریتم تغییر میانگین با استفاده از کلاس MeanShift

  و مانند نمونه پیاده‌سازی می‌شود:

1# mean shift clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.cluster import MeanShift
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = MeanShift()
12# fit model and predict clusters
13yhat = model.fit_predict(X)
14# retrieve unique clusters
15clusters = unique(yhat)
16# create scatter plot for samples from each cluster
17for cluster in clusters:
18	# get row indexes for samples with this cluster
19	row_ix = where(yhat == cluster)
20	# create scatter of these samples
21	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
22# show the plot
23pyplot.show()

پس از اجرای قطعه کد بالا، نموداری مشابه تصویر زیر حاصل می‌شود:

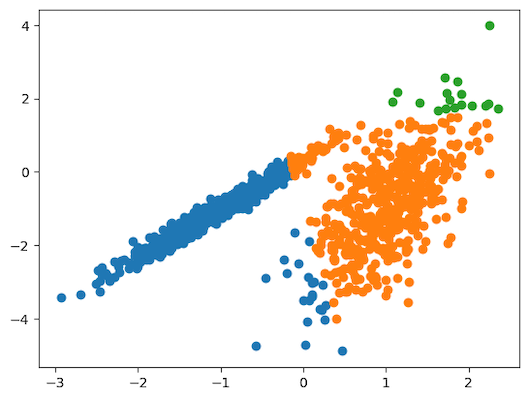
همان‌طور که در نمودار نقطه‌ای نیز مشخص است، نمونه‌ها در سه خوشه مجزا گروه‌بندی شده‌اند.

۴. الگوریتم خوشه بندی DBSCAN

روش خوشه‌بندی به اصطلاح DBSCAN، مخفف عبارت (Density-Based Spatial Clustering of Applications with Noise) بوده که در واقع نوعی الگوریتم خوشه‌بندی فضایی مبتنی‌بر چگالی، برای کاربردهایی است که با داده‌های نویزی سروکار دارند. خوشه‌بندی DBSCAN نوع پیشرفته‌تری از الگوریتم تغییر میانگین با مزایای بیشتر است که مانند زیر کار می‌کند:

1. شروع کار الگوریتم از موقعیتی دلخواه و ملاقات نشده است. سپس با در نظر گرفتن فاصله‌ای به عنوان $$ epsilon $$، نمونه‌هایی که در همسایگی موقعیت شروع قرار دارند، استخراج می‌شوند.
2. با در نظر گرفتن حد آستانه‌ای به نام minPoints، اگر تعداد نمونه‌های همسایه به اندازه کافی باشد، فرایند خوشه‌بندی آغاز شده و نقطه داده شروع به انواع اولین نمونه در خوشه جدید قرار می‌گیرد. در غیر این‌صورت، نمونه به عنوان داده نویزی برچسب‌گذاری می‌شود. حتی نمونه‌های نویزی نیز ممکن است در مراحل بعدی در خوشه‌ها قرار بگیرند و در هر دو حالت، چه عضوی از خوشه باشند و چه نباشند، به عنوان نمونه‌ای «ملاقات شده» (Visited) نشانه‌گذاری می‌شوند.
3. در قدم بعدی، نقاطی که در فاصله‌ای برابر یا کمتر از $$ epsilon $$ با اولین نمونه خوشه قرار داشته باشند، به عنوان همسایگان آن نمونه در همان خوشه قرار می‌گیرند. سپس فرایند محاسبه فاصله $$ epsilon $$ برای همه نقاط داده‌ای که به تازگی عضو خوشه شده‌اند نیز تکرار می‌شود.
4. مراحل ۲ و ۳ تا جایی تکرار می‌شوند که تمامی نقاط داده ملاقات و برچسب‌گذاری شده باشند.
5. پس از تکمیل شدن اولین خوشه، نمونه‌ای دیگر که تا به حال ملاقات نشده، انتخاب و مجدد مراحل ۱ تا ۴ برای کشف خوشه یا داده نویزی جدید تکرار می‌شوند. این فرایند را تا زمانی تکرار می‌کنیم که تمامی نقاط داده ملاقت شده و یکی از برچسب‌های عضو خوشه یا داده نویزی را دریافت کرده باشند.

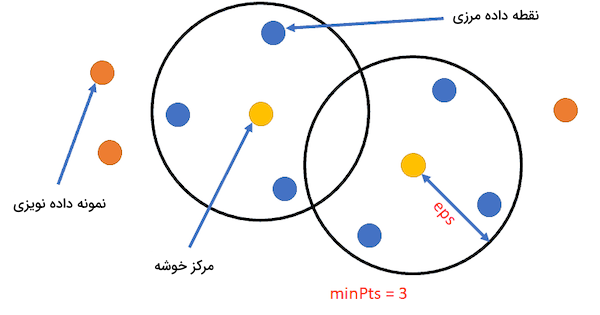
الگوریتم خوشه‌بندی DBSCAN نسبت به سایر روش‌ها شامل مزایای بیشتری است. در این الگوریتم نیازی نیست تعداد خوشه‌ها در ابتدا مشخص شوند. همچنین برخلاف روش تغییر میانگین که داده‌های نامعمول را نیز در خوشه‌ها قرار می‌دهد، الگوریتم DBSCAN نمونه‌های پرت را به عنوان داده‌های نویزی علامت‌گذاری می‌کند. علاوه‌بر آن، شکل خوشه‌ها نیز پیرو قرارداد خاصی نبوده و ممکن است هر شکل دلخواهی داشته باشند. با وجود همه این مزایا، وقتی تراکم خوشه‌ها یکسان نباشد، عملکرد سایر روش‌ها از الگوریتم DBSCAN بهتر است. زیرا در خوشه‌هایی با توزیع تراکم متفاوت، فاصله $$ epsilon $$ و حد آستانه minPoints که در ابتدا تعریف می‌کنیم، برای هر خوشه متفاوت خواهد بود. به دلیل دشواری انتخاب فاصله $$ epsilon $$، این مشکل در داده‌هایی با ابعاد بالا نیز نمایان می‌شود. پیاده‌سازی الگوریتم DBSCAN در کتابخانه scikit-learn، از طریق کلاس DBSCAN

  و پارامترهای eps

  و min_samples

  که به ترتیب بیانگر فاصله $$ epsilon $$ و حد آستانه minPoints هستند انجام می‌شود:

1# dbscan clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.cluster import DBSCAN
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = DBSCAN(eps=0.30, min_samples=9)
12# fit model and predict clusters
13yhat = model.fit_predict(X)
14# retrieve unique clusters
15clusters = unique(yhat)
16# create scatter plot for samples from each cluster
17for cluster in clusters:
18	# get row indexes for samples with this cluster
19	row_ix = where(yhat == cluster)
20	# create scatter of these samples
21	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
22# show the plot
23pyplot.show()

همان‌طور که در قطعه کد بالا مشاهده می‌کنید، مقدار eps

  برابر با 0.30 و min_samples

  برابر با 9 قرار داده شده است. این مقادیر برای هر مسئله متفاوت بوده و امکان دارد برای پروژه شما متفاوت باشد.

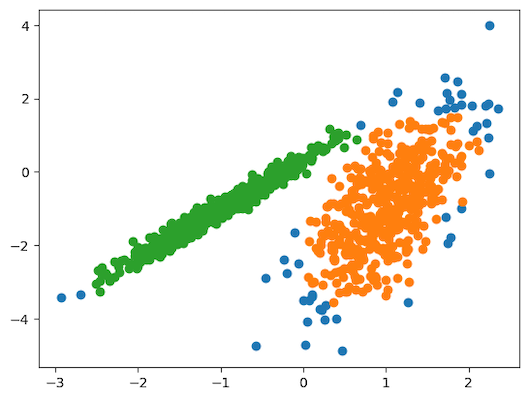
با توجه به نمودار فوق، سه خوشه مختلف توسط الگوریتم DBSCAN شناسایی شده‌اند. اگر چه با تنظیم دقیق‌تر پارامترها، گروه‌بندی بهتری نیز حاصل می‌شود.

۵. الگوریتم خوشه بندی مخلوط گاوسی

استفاده سطحی و ساده الگوریتم K-Means از مقدار میانگین نمونه‌ها برای تعیین مراکز خوشه، از جمله معایب اصلی این روش به حساب می‌آید. دلیل این موضوع با توجه به شکل زیر قابل فهم است:

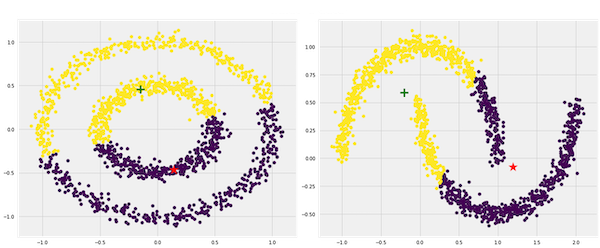
در شکل سمت چپ، دو خوشه دایره‌ای با شعاع متفاوت را مشاهده می‌کنید که میانگین یکسانی دارند. الگوریتم K-Means قادر به حل چنین مسائلی نیست. همچنین اگر مانند شکل سمت راست، خوشه‌ها شکل دایره‌ای نداشته باشند، الگوریتم K-Means نمی‌تواند عمل خوشه‌بندی را انجام دهد.

انعطاف‌پذیری «مدل‌های مخلوط گاوسی» (Gaussian Mixture Models | GMMs) از الگوریتم K میانگین بیشتر است. در مدل‌های مخلوط گاوسی، توزیع تمامی نقاط داده از نوع «گاوسی» (Gaussian) در نظر گرفته می‌شود. بدین ترتیب، دو پارامتر «میانگین» (Mean) و «انحراف معیار» (Standard Deviation) برای توصیف شکل خوشه‌ها در این الگوریتم مورد استفاده قرار می‌گیرند. در نتیجه از آن‌جایی که انحراف معیار برای دو محور x و y محاسبه می‌شود، هر نوع شکل بیضوی برای خوشه‌ها قابل تصور است. برای پیدا کردن پارامترهای گاوسی مانند میانگین و انحراف معیار، از نوعی الگوریتم بهینه‌سازی به نام «بیشینه‌سازی امید ریاضی» (Expectation-Maximization | EM) استفاده می‌شود. سپس پارامترهای انتخابی به مدل مخلوط گاوسی (GMM) منتقل شده و الگوریتم به کار خود ادامه می‌دهد:

1. مانند الگوریتم K-Means، تعداد خوشه‌ها را مشخص کرده و پارامترهای توزیع گاوسی مناسب هر خوشه را مقداردهی اولیه می‌کنیم. با بررسی مختصر داده‌ها، می‌توان دید خوبی نسبت به مقادیر اولیه پارامترهای گاوسی به‌دست آورد. گرچه الگوریتم مخلوط گاوسی در شروع عملکرد قابل قبولی ندارد اما، خیلی سریع به پاسخ بهینه می‌رسد.
2. سپس و با فرض در اختیار داشتن توزیع گاوسی هر خوشه، احتمال عضویت هر نمونه داده در خوشه متناظر محاسبه می‌شود. هر چه نمونه داده به مرکز گاوسی نزدیک‌تر باشد، یعنی احتمال قرار گرفتن آن در خوشه بیشتر است. رویکردی واضح از نظر شهودی، چرا که در توزیع گاوسی، فرض بر تراکم داده‌ها در قسمت مرکز خوشه گذاشته می‌شود.
3. مطابق با احتمالات به‌دست آمده، مجموعه‌ای جدید از پارامترهای گاوسی را محاسبه کرده و احتمال نقاط داده موجود در خوشه‌ها را بیشینه می‌کنیم. مقدار پارامترهای جدید، با استفاده از جمع وزن‌دار نمونه‌ها محاسبه می‌شود که وزن‌ها، در واقع همان مقادیر احتمالی وجود نقاط داده در خوشه هستند.
4. مراحل ۲ و ۳ تا زمانی تکرار می‌شوند که مقادیر توزیع گاوسی از یک اجرا به اجرای دیگر تغییر قابل ملاحظه‌ای نداشته و در واقع به همگرایی برسیم.

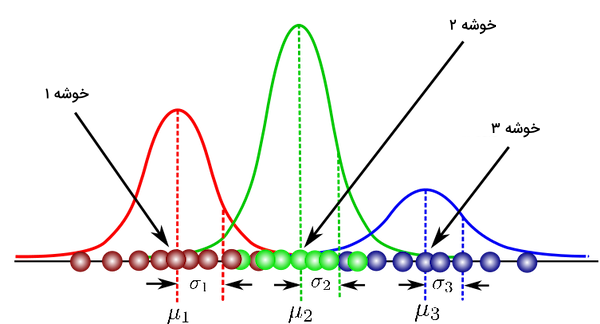
مدل‌های مخلوط گاوسی از دو مزیت عمده در مقایسه با سایر روش‌ها برخوردار هستند. مقدار «کواریانس خوشه» (Cluster Covariance) در این مدل‌ها، نسبت به روشی مانند K-Means به مراتب انعطاف‌پذیرتر است. به‌خاطر وجود معیاری به نام انحراف معیار، محدودیتی برای شکل خوشه‌ها وجود ندارد. الگوریتم K-Means در واقع نوع خاصی از مدل مخلوط گاوسی (GMM) است، که در آن کواریانس هر خوشه در تمامی ابعاد به سمت صفر میل می‌کند. همچنین از آن‌جایی که در این روش از احتمالات استفاده می‌شود، هر نمونه می‌تواند در چندین خوشه مختلف قرار بگیرد. به عنوان مثال اگر نمونه داده‌ای در مرز مشترک دو خوشه قرار داشته باشد، می‌گوییم به احتمال X درصد به کلاس ۱ و Y درصد به کلاس ۲ تعلق دارد. همان‌طور که در قطعه کد زیر نیز ملاحظه می‌کنید، الگوریتم مخلوط گاوسی از طریق کلاس GaussianMixture

  پیاده‌سازی شده و پارامتر ورودی n_components

، تعداد تقریبی خوشه‌ها را مشخص می‌کند:

1# gaussian mixture clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.mixture import GaussianMixture
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = GaussianMixture(n_components=2)
12# fit the model
13model.fit(X)
14# assign a cluster to each example
15yhat = model.predict(X)
16# retrieve unique clusters
17clusters = unique(yhat)
18# create scatter plot for samples from each cluster
19for cluster in clusters:
20	# get row indexes for samples with this cluster
21	row_ix = where(yhat == cluster)
22	# create scatter of these samples
23	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
24# show the plot
25pyplot.show()

پس از اجرای پیاده‌سازی بالا، مدل بر مجموعه‌داده آموزشی برازش شده و هر نمونه داده در خوشه‌ای مجزا گروه‌بندی می‌شود. نمودار نقطه‌ای حاصل، مانند شکل زیر است:

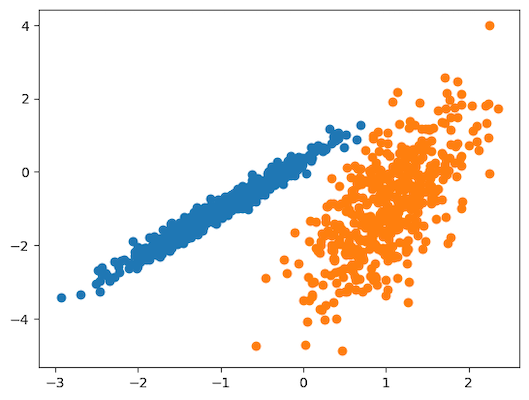
همان‌طور که در تصویر نیز مشخص است، عمل خوشه‌بندی بدون حتی یک مورد خطا انجام شده و نقاط داده در دو گروه طبقه‌بندی شده‌اند.

۶. الگوریتم خوشه بندی سلسله مراتبی ترکیبی

خوشه‌بندی سلسله مراتبی، متشکل از دو نوع بالا-پایین یا «تقسیمی» (Divisive) و پایین-بالا یا «ترکیبی» (Agglomerative) است. الگوریتم پایین-بالا در ابتدا هر نمونه داده را به عنوان یک خوشه در نظر گرفته و از پایین به‌طور متوالی، جفت خوشه‌ها را باهم ادغام می‌کند تا در نهایت یک خوشه، حاوی تمامی نمونه‌ها باقی بماند. سلسله مراتبی از خوشه‌ها که در غالب یک درخت یا «دندروگرام» (Dendrogram) نمایش داده می‌شوند. ریشه درخت که در بالاترین بخش قرار می‌گیرد، همان خوشه نهایی با تمامی نمونه‌ها است و برگ‌ها نیز تک نمونه‌هایی هستند که در ابتدا به عنوان خوشه در نظر گرفته می‌شوند. مراحل اجرای الگوریتم خوشه‌بندی سلسله مراتبی ترکیبی به شرح زیر است:

1. ابتدا با تمامی نقاط داده مانند یک خوشه رفتار می‌کنیم. به عنوان مثال اگر مجموعه‌داده ما ۱۰ نمونه داشته باشد، یعنی ۱۰ خوشه داریم. سپس یک معیار فاصله برای اندازه‌گیری فاصله میان دو خوشه انتخاب می‌کنیم. برای نمونه، معیار «پیوند میانگین» (Average Linkage)، از میانگین فاصله میان نقاط داده خوشه اول و خوشه دوم، به عنوان فاصله استفاده می‌کند.
2. در هر تکرار از الگوریتم، دو خوشه را با یک‌دیگر ترکیب می‌کنیم. دو خوشه‌ای باهم ترکیب می‌شوند که کمترین پیوند میانگین را داشته باشند. بر اساس این معیار، هر نمونه در خوشه اول، کمترین فاصله را با نمونه متناظر در خوشه دوم دارد و به همین خاطر است که شبیه به یک‌دیگر هستند.
3. مرحله شماره ۲ تا زمانی تکرار می‌شود که به ریشه درخت رسیده و تنها یک خوشه، شامل تمامی نقاط داده داشته باشیم. در این الگوریتم، تعداد خوشه‌های نهایی به خودمان بستگی دارد و می‌توانیم هر زمان که خواستیم، فرایند ادغام خوشه‌ها یا همان تشکیل درخت را متوقف کنیم.

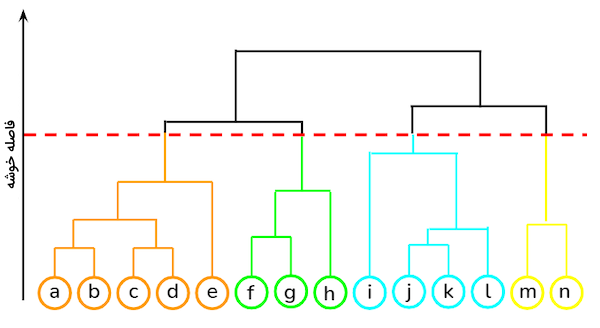
الگوریتم خوشه‌بندی سلسله مراتبی ترکیبی، نه تنها نیازی به تعیین اولیه تعداد خوشه‌ها ندارد، بلکه از آن‌جایی که در حال ایجاد ساختاری درختی هستیم، تعداد خوشه‌های نهایی نیز به دلخواه مشخص می‌شود. همچنین حساسیتی به نوع معیار فاصله نداشته و بر خلاف سایر الگوریتم‌ها،‌ با هر معیاری، نتیجه قابل قبولی ارائه می‌دهد. از جمله موارد کاربردی این الگوریتم،‌ زمانی است که مجموعه‌داده شما ساختاری سلسله مراتبی داشته و قصد دارید آن ساختار را بازیابی کنید. مزیت روش ترکیبی همزمان باعث افت کارآمدی شده و برعکس الگوریتم‌های K-Means و GMM که پیچیدگی زمانی خطی دارند، زمان اجرای این الگوریتم برابر با $$ O(n^3) $$ است. در مرحله پیاده‌سازی، کلاس AgglomerativeClustering

  به کمک ما آمده و مانند زیر با پارامتر ورودی n_clusters

  که تخمینی از تعداد خوشه‌ها است، فراخوانی می‌شود:

1# agglomerative clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.cluster import AgglomerativeClustering
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = AgglomerativeClustering(n_clusters=2)
12# fit model and predict clusters
13yhat = model.fit_predict(X)
14# retrieve unique clusters
15clusters = unique(yhat)
16# create scatter plot for samples from each cluster
17for cluster in clusters:
18	# get row indexes for samples with this cluster
19	row_ix = where(yhat == cluster)
20	# create scatter of these samples
21	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
22# show the plot
23pyplot.show()

پس از اجرای قطعه کد بالا، نموداری نقطه‌ای مانند تصویر زیر به‌دست می‌آید:

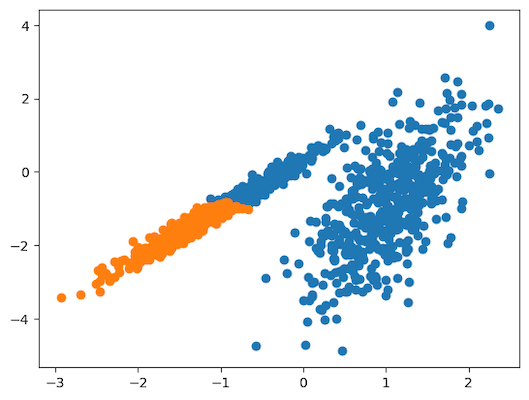
همان‌طور که در تصویر مشاهده می‌کنید، گروه‌بندی معقولی از داده‌ها صورت گرفته است.

۷. الگوریتم خوشه بندی BIRCH

واژه BIRCH مخفف عبارت (Balanced Iterative Reducing and Clustering using Hierarchies) و به معنی خوشه‌بندی و کاهش متوازن با بهره‌گیری از سازوکاری سلسله مراتبی است. در مقایسه با K-Means، الگوریتم خوشه‌بندی BIRCH عملکرد بهتری در مقابل مجموعه‌داده‌های بزرگ از خود نشان می‌دهد. این الگوریتم، نمونه داده‌ها را به شکل خوشه درمی‌آورد که هر خوشه شامل اطلاعات مربوط به توزیع نقاط داده است. به‌طور معمول، از الگوریتم BIRCH در ترکیب با دیگر روش‌های خوشه‌بندی استفاده می‌شود؛ زیرا خروجی این الگوریتم را می‌توان به عنوان ورودی سایر الگوریتم‌ها در نظر گرفت. الگوریتم خوشه‌بندی BIRCH تنها بر روی داده‌های عددی کار می‌کند و از همین مورد به عنوان یکی از معایب اصلی آن یاد می‌شود. اگر داده‌های شما هر نوع دیگری به‌جز عددی باشند، امکان استفاده از الگوریتم BIRCH وجود ندارد؛ مگر این‌که داده‌ها را به نوع عددی تبدیل کنید.

کلاس Birch

  از کتابخانه scikit-learn، امکان پیاده‌سازی این الگوریتم را مهیا می‌سازد. دو پارامتر threshold

  و n_clusters

  به عنوان ورودی این کلاس مقداردهی می‌شوند که به ترتیب بیانگر حد آستانه تعداد گره‌های برگ یک شاخه و تخمینی از تعداد خوشه‌ها هستند:

1# birch clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.cluster import Birch
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = Birch(threshold=0.01, n_clusters=2)
12# fit the model
13model.fit(X)
14# assign a cluster to each example
15yhat = model.predict(X)
16# retrieve unique clusters
17clusters = unique(yhat)
18# create scatter plot for samples from each cluster
19for cluster in clusters:
20	# get row indexes for samples with this cluster
21	row_ix = where(yhat == cluster)
22	# create scatter of these samples
23	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
24# show the plot
25pyplot.show()

پس از اجرای قطعه کد بالا، با نموداری مشابه تصویر زیر در خروجی مواجه می‌شوید:

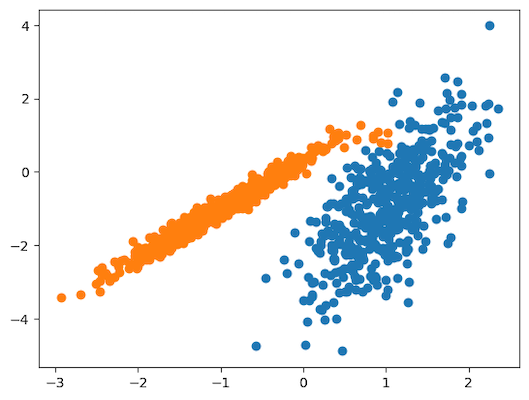
همان‌طور که در نمودار نقطه‌ای ملاحظه می‌کنید، عمل خوشه‌بندی به خوبی انجام شده است.

۸. الگوریتم خوشه بندی انتشار وابستگی

نحوه خوشه‌بندی الگوریتم «انتشار وابستگی» (Affinity Propagation) متفاوت از دیگر الگوریتم‌های خوشه‌بندی است. در این روش،‌ تمامی نمونه‌ها باهم در ارتباط هستند و پس از شناسایی شباهت میان یک‌دیگر، فرایند خوشه‌بندی انجام می‌شود. همزمان با برقراری ارتباط، مجموعه‌ای از داده‌ها با عنوان «نمونه‌های شاخص» (Exemplars) پیدا شده که در واقع همان خوشه‌ها را تشکیل می‌دهند.

یک نمونه شاخص زمانی پدیدار می‌شود که ارتباط میان نقاط داده شکل گرفته و بر سر بهترین نمونه‌ای که می‌تواند به عنوان خوشه شناخته شود، به توافق رسیده باشند. استفاده از الگوریتم انتشار وابستگی در مسائلی مانند «بینایی ماشین» (Computer Vision) که تعداد دقیق خوشه‌ها مشخص نیست پیشنهاد می‌شود. پیاده‌سازی این الگوریتم در زبان برنامه‌نویسی پایتون، از طریق کلاس AffinityPropagation

  و مانند زیر صورت می‌گیرد:

1# affinity propagation clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.cluster import AffinityPropagation
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = AffinityPropagation(damping=0.9)
12# fit the model
13model.fit(X)
14# assign a cluster to each example
15yhat = model.predict(X)
16# retrieve unique clusters
17clusters = unique(yhat)
18# create scatter plot for samples from each cluster
19for cluster in clusters:
20	# get row indexes for samples with this cluster
21	row_ix = where(yhat == cluster)
22	# create scatter of these samples
23	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
24# show the plot
25pyplot.show()

نمودار نقطه‌ای زیر، نتیجه اجرای قطعه کد بالا است:

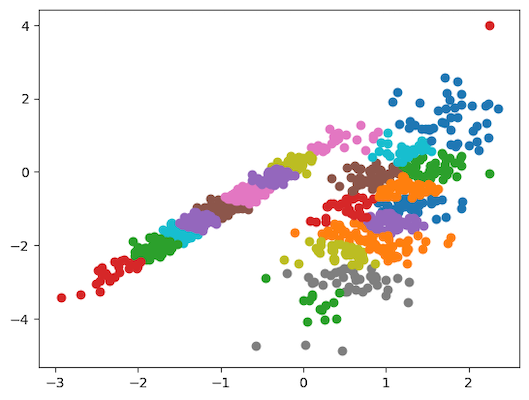
همان‌طور که در نمودار نیز با رنگ‌های مختلف نشان داده شده است، داده‌ها در ۱۰ کلاس مجزا توسط الگوریتم انتشار وابستگی دسته‌بندی شده‌اند.

۹. الگوریتم خوشه بندی OPTICS

واژه OPTICS مخفف عبارت (Ordering Points to Identify the Clustering Structure) به معنی مرتب‌سازی نقاط داده به‌منظور شناسایی ساختار خوشه‌بندی است. روش OPTICS از جمله الگوریتم های خوشه بندی مبتنی‌بر چگالی است که شباهت زیادی با الگوریتم DBSCAN دارد. با این تفاوت که بر خلاف DBSCAN، این الگوریتم می‌تواند در نواحی با نسبت تراکم متغیر نیز خوشه‌ها را پیدا کند. نحوه کار الگوریتم خوشه‌بندی OPTICS به این صورت است که ابتدا نقاط داده را مرتب‌سازی کرده و سپس نزدیک‌ترین نمونه‌ها را به عنوان همسایه نشانه‌گذاری می‌کند. در نتیجه، فرایند خوشه‌بندی راحت‌تر انجام شده و مشابه الگوریتم DBSCAN، هر نمونه داده تنها یک مرتبه پردازش می‌شود.

در مثال زیر، نحوه پیاده‌سازی الگوریتم خوشه‌بندی OPTICS با استفاده از کلاس OPTICS

  را ملاحظه می‌کنید. همانند روش DBSCAN، در این کلاس نیز دو پارامتر eps

  و min_samples

  به عنوان ورودی تعیین می‌شوند:

1# optics clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.cluster import OPTICS
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = OPTICS(eps=0.8, min_samples=10)
12# fit model and predict clusters
13yhat = model.fit_predict(X)
14# retrieve unique clusters
15clusters = unique(yhat)
16# create scatter plot for samples from each cluster
17for cluster in clusters:
18	# get row indexes for samples with this cluster
19	row_ix = where(yhat == cluster)
20	# create scatter of these samples
21	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
22# show the plot
23pyplot.show()

نموداری که در تصویر زیر مشاهده می‌کنید، نتیجه اجرای قطعه کد بالا می‌باشد:

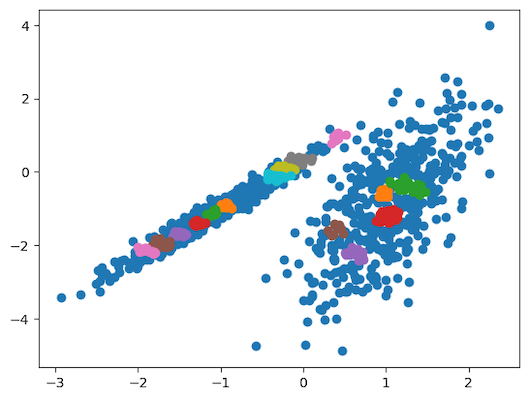
با توجه به نمودار، الگوریتم OPTICS داده‌ها را در ۱۰ دسته مختلف تفکیک کرده است.

۱۰. الگوریتم خوشه بندی طیفی

رویکرد «خوشه‌بندی طیفی» (Spectral Clustering) در واقع نوعی کلاس عمومی از روش‌های خوشه‌بندی است که منشأ آن «جبر خطی» (Linear Algebra) می‌باشد. در این الگوریتم از «بردارهای ویژه» (Eigen Vectors) حاصل از فاصله میان نقاط داده استفاده می‌شود. کلاس SpectralClustering

  وظیفه پیاده‌سازی الگوریتم خوشه‌بندی طیفی را بر عهده دارد و پارامتر n_clusters

  را به عنوان ورودی می‌پذیرد:

1# spectral clustering
2from numpy import unique
3from numpy import where
4from sklearn.datasets import make_classification
5from sklearn.cluster import SpectralClustering
6from matplotlib import pyplot
7
8# define dataset
9X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
10# define the model
11model = SpectralClustering(n_clusters=2)
12# fit model and predict clusters
13yhat = model.fit_predict(X)
14# retrieve unique clusters
15clusters = unique(yhat)
16# create scatter plot for samples from each cluster
17for cluster in clusters:
18	# get row indexes for samples with this cluster
19	row_ix = where(yhat == cluster)
20	# create scatter of these samples
21	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
22# show the plot
23pyplot.show()

اجرای قطعه کد بالا، مدلی برازش شده بر مجموعه‌داده آموزشی و داده‌هایی خوشه‌بندی شده را نتیجه می‌دهد. همان‌طور که در نمودار نقطه‌ای زیر ملاحظه می‌کنید، نقاط داده در دو خوشه گروه‌بندی و با دو رنگ متفاوت نیز ترسیم شده‌اند:

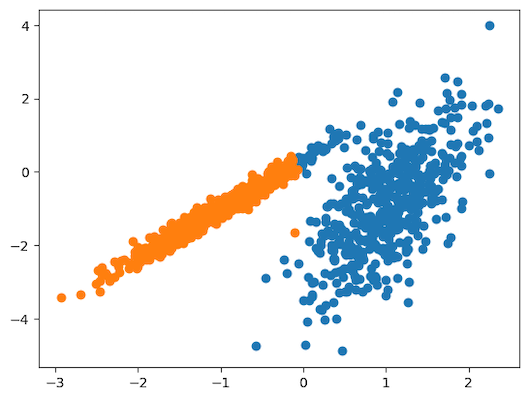
کاربرد الگوریتم های خوشه بندی

الگوریتم های خوشه بندی در کاربردهای متنوعی به‌منظور آماده‌سازی داده‌ها برای مدل‌های یادگیری ماشین مورد استفاده قرار می‌گیرند. برخی از این کاربردها را در ادامه فهرست کرده‌ایم:

1. «تقسیم‌بندی بازار» (Market Segmentation): کسب‌وکارها برای درک جامعه مخاطب، باید بازار هدف خود را به گروه‌هایی کوچک‌تر بخش‌بندی کنند. الگوریتم های خوشه بندی، افراد شبیه به یک‌دیگر را به عنوان همسایه شناسایی کرده و محصولاتی مشابه را به آن‌ها پیشنهاد می‌دهند.
2. «بازاریابی خرده‌فروشی» (Retail Marketing) و فروش: در بازاریابی از الگوریتم های خوشه بندی برای فهمیدن رفتار مشتری و در ادامه ارائه پیشنهاد استفاده می‌شود. این الگوریتم‌ها، مشتریان با ویژگی‌ها و احتمالات خرید مشابه را گروه‌بندی می‌کنند. در نتیجه، جامعه مخاطب تبلیغات به درستی شناسایی می‌شود.
3. تحلیل شبکه‌های اجتماعی: توافقات کمی و کیفی اجتماعی از طریق شبکه و «نظریه گراف» (Graph Theory) مورد بررسی قرار می‌گیرند. بهره‌گیری از الگوریتم های خوشه بندی برای کشف تعاملات میان کاربران ضرورت دارد.
4. «طبقه‌بندی ترافیک شبکه» (Network Traffic Classification): الگوریتم های خوشه بندی، منابع ترافیک شبکه‌ای مختلف را طبقه‌بندی می‌کنند. هر خوشه وظیفه دسته‌بندی انواع ترافیک‌ها را بر عهده دارد. با کسب اطلاعات دقیق درباره منابع ترافیکی، راحت‌تر می‌توان برای مدیریت ظرفیت برنامه‌ریزی کرد.
5. «فشرده‌سازی تصاویر» (Image Compression): یکی دیگر از کاربردهای الگوریتم های خوشه بندی، ذخیره‌سازی نوع فشرده شده تصاویر بدون از دست دادن کیفیت است.

1. «پردازش داده» (Data Processing): داده‌ها را می‌توان به شکل خوشه درآورد. بدین ترتیب، فضای زیادی ذخیره شده و بازیابی داده‌ها از طریق ویژگی‌هایی همچون تاریخ و زمان ممکن می‌شود.
2. قانون‌گذاری برای سرویس‌های نمایشی: با استفاده از الگوریتم های خوشه بندی، بینندگان با رفتار و علایق مشابه شناسایی می‌شوند. شرکت «نتفلیکس» (Netflix) و دیگر پلتفرم‌ها، کاربران را بر اساس پارامترهایی مانند ژانر فیلم و میزان تماشا در روز در گروه‌های مجزا خوشه‌بندی می‌کنند. در نتیجه، نمایش آگهی و پیشنهاد محتوای جدید به کاربران، هدفمند می‌شود.
3. «نشانه‌گذاری پیشنهادات» (Tagging Suggestions): شناسایی الگوی جستجو و نشانه‌گذاری موارد پرتکرار، با استفاده از الگوریتم های خوشه بندی امکان‌پذیر است. پس از هر بار جستجوی یک عبارت، معادلی به عنوان برچسب آن در مجموعه‌داده انتخاب شده و از طریق یک معیار شباهت خوشه‌بندی می‌شوند.
4. علوم حیاتی و خدمات درمانی: الگوریتم های خوشه بندی، ژن‌ها را بر اساس رفتارهای مشابه جانداران سازمان‌دهی می‌کنند. تشخیص سلول‌های سرطانی از روی تصاویر پزشکی، یکی دیگر از کاربردهای خوشه‌بندی است.
5. شناسایی محتوای خوب و بد: بهره‌گیری از الگوریتم های خوشه بندی، کاربردی مانند تفکیک محتوای جعلی از واقعی را ممکن می‌سازد.

همزمان با افزایش روزافزون داده‌ها، کاربرد انواع روش‌های یادگیری ماشین بیشتر شده و الگوریتم های خوشه بندی نیز از این قاعده مستثنا نیستند.

سوالات متداول

پس از آن‌که یاد گرفتیم خوشه‌بندی چیست و با انواع الگوریتم های خوشه بندی آشنا شدیم، حال زمان خوبی است تا در این بخش از مطلب مجله فرادرس، به چند مورد از پرسش‌های متداول این حوزه پاسخ دهیم.

تعریف الگوریتم خوشه بندی چیست؟

الگوریتم های خوشه بندی، زیرمجموعه‌ای از روش‌های نظارت نشده هستند که با پردازش تعداد زیادی از داده‌های بدون برچسب و استفاده از معیارهای شباهت، نمونه‌های جدید را طبقه‌بندی می‌کنند.

چه الگوریتمی در خوشه بندی بهترین است؟

هر کدام از الگوریتم های خوشه بندی مزایا و معیاب خود را داشته و انتخاب مناسب این الگوریتم‌ها به نوع مسئله و مجموعه‌داده شما بستگی دارد.

الگوریتم های خوشه بندی در چه دسته هایی قرار می‌گیرند؟

از جمله اصلی‌ترین روش‌های خوشه‌بندی می‌توان به روش‌های مبتنی‌بر چگالی، مبتنی‌بر توزیع، مبتنی‌بر مرکز و سلسله مراتبی اشاره کرد.

خوشه بندی در کدام گروه از روش های یادگیری ماشین قرار دارد؟

الگوریتم های خوشه بندی در واقع رویکردی نظارت نشده هستند که از تفکیک داده‌ها به عنوان هدف اصلی آن‌ها یاد می‌شود.

جمع‌بندی

خوشه‌بندی بخشی جدا نشدنی از «داده کاوی» (Data Mining) و یادگیری ماشین است. الگوریتم هایی که داده‌ها را بر اساس ویژگی‌های مشترک، در گروه‌هایی مجزا بخش‌بندی کرده و به شما این امکان را می‌دهند تا پیش‌بینی دقیق‌تری از رفتار کاربران داشته باشید. در این مطلب از مجله فرادرس، با انواع الگوریتم های خوشه بندی آشنا شدیم و نحوه پیاده‌سازی آن‌ها را نیز یاد گرفتیم. نتایج حاصل از خوشه‌بندی،‌ زمینه‌ساز نوآوری‌های بی‌شماری در آینده نزدیک است.