تعیین علامت یکی از تکنیکهای مهم و کاربردی در ریاضی است. با تعیین علامت میتوان وضعیت یک تابع را در اطراف ریشههایش بررسی کرد. تعیین علامت عبارت کسری میتواند شامل توابع چندجملهای، درجه دوم، قدرمطلق، نمایی، مثلثاتی، جزء صحیح و رادیکالی باشد. در این مطلب از مجله فرادرس به بررسی همه این موارد همراه با مثالهای متنوع میپردازیم. اگر به این موضوع علاقهمند هستید این مطلب را تا انتها مطالعه کنید.
تعیین علامت عبارت کسری
در توابع کسری ممکن است انواع توابع مانند قدرمطلق، چندجملهای، مثلثاتی، درجه دوم و غیره وجود داشته باشد که تعیین علامت هرکدام از آنها را با ذکر مثال در قسمتهای بعدی توضیح داده شده است. در تعیین علامت عبارت کسری باید ریشههای صورت و مخرج را جداگانه محاسبه و در یک جدول تعیین علامت کرد و سپس علامتها را در هر ستون در هم ضرب کنیم تا کل کسر تعیین علامت شود. نکته مهم در تعیین علامت عبارت کسری توجه به ریشههای مخرج است که باید آنها را با نماد بینهایت در جدول نشان دهیم. برای درک بهتر این قسمت به مثالهای زیر توجه کنید.
مثال اول تعیین علامت عبارت کسری
میخواهیم کسر $$frac{1x^{2}}{2}+frac{3}{4}x-frac{1}{8}=y$$ را تعیین علامت کنیم.
پاسخ:
ابتدا باید تمام جملات را با هم جمع کنیم تا یک کسر واحد داشته باشیم.
$$frac{x^{2}}{2}+frac{3}{4}x-frac{1}{8}=0$$
$$frac{x^{2}}{2}+frac{3x}{4}-frac{1}{8}=0$$
مخرج مشترک میگیریم.
$$frac{4}{4} times frac{x^{2}}{2}+frac{2}{2} times frac{3x}{4}+frac{-1}{8}=0$$
$$frac{4x^{2}}{8}+frac{2 times 3x}{8}+frac{-1}{8}=0$$
$$frac{4x^{2}+2 times 3x-1}{8}=0$$
$$frac{4x^{2}+6x-1}{8}=0$$
مخرج کسر را از بین میبریم.
$$8 times frac{4x^{2}+6x-1}{8}=0$$
به یک معادله درجه دوم میرسیم.
$$4x^{2}+6x-1=0$$
حال با روش دلتا ریشههای آن را مشخص میکنیم.
$$x=frac{-b pm sqrt{b^{2}-4ac}}{2a} $$
$$x=frac{-6 pm 2sqrt{13}}{8}$$
چون دلتا مثبت می شود پس معادله دو ریشه حقیقی متمایز دارد.
ریشههای معادله به صورت زیر است:
$$x=frac{sqrt{13}-3}{4}$$
$$x=frac{-sqrt{13}-3}{4}$$
اکنون مطابق جدول زیر تعیین علامت را انجام میدهیم:
$$boxed{begin{matrix}x & & frac{-sqrt{13}-3}{4} & &frac{sqrt{13}-3}{4} & \y & + & 0 & – &0 & +end{matrix}}$$
همان گونه که در این مثال مشاهده کردید، عبارت کسری در ابتدای سوال پس از ساده سازی به یک معادله درجه دوم تبدیل شد و آن را تعیین علامت کردیم.

مثال دوم تعیین علامت کسری
عبارت $$y=frac{mid x-9mid}{2x^2-3}$$ را تعیین علامت کنید.
پاسخ:
در این عبارت کسری، در صورت قدرمطلق و در مخرج معادله درجه دوم داریم و باید ریشه هرکدام را جداگانه محاسبه کنیم سپس تعیین علامت کنیم.
ابتدا با قدرمطلق شروع میکنیم و باید آن را مساوی با صفر قرار دهیم.
$$mid x-9mid=0$$
$$x=9$$
سپس ریشههای معادله درجه دوم که در مخرج کسر قرار دارد را محاسبه میکنیم.
$$2x^2-3=0$$
دلتا در معادله فوق مثبت و برابر ۲۴ است بنابراین دو ریشه حقیقی و متمایز دارد.
$$x=pmsqrt{frac{3}{2}}$$
سپس مطابق جدول زیر صورت و مخرج را جداگانه تعیین علامت میکنیم و در مرحله بعد با ضرب علامت در هر ستون کل کسر را تعیین علامت میکنیم.
$$boxed{begin{matrix}x & &x=-sqrt{frac{3}{2}} & & x=+sqrt{frac{3}{2}} & & 9& \mid x-9mid &+ & + & + & + &+ & 0 &+\2x^2-3 & + & 0 &- & 0 & + & + &+\ y& + & infty & – & infty & +&0 &+end{matrix}}$$
مثال سوم تعیین علامت کسری
میخواهیم کسر $$y=(frac{sin(x)}{1+cos(x)})$$ را در بازه $$-pi$$ تا $$+pi$$ تعیین علامت کنیم.
پاسخ:
در صورت و مخرج عبارت فوق توابع مثلثاتی داریم. ریشههای صورت و مخرج را جداگانه محاسبه میکنیم و سپس تعیین علامت میکنیم.
ابتدا ریشههای صورت را محاسبه میکنیم. همان طور که در قسمت مربوطه اشاره شد، ریشههای تابع سینوس به صورت زیر است:
$$sin x=pm npi$$
که به ازای تمام مقادیر $$n$$ دارای ریشه است.
ریشههای عبارت مخرج به شکل زیر است:
$$x=2npi pm pi$$
که به ازای تمام مقادیر فرد $$n$$ دارای ریشه است. جدول زیر تعیین علامت کلی را نشان میدهد.
$$boxed{begin{matrix}x & &-pi & & 0& & +pi& \sin x & + & 0 & – & 0 & + &0 & -\ 1+ cos x& + & 0 & + &+ & +&0 &+ \ y&+ & infty & – &0 & +&infty& -end{matrix}}$$
مثال چهارم تعیین علامت کسری
عبارت $$(frac{tan(x)}{sec(x)})=y$$ را در بازه $$(-pi,+pi)$$ تعیین علامت کنید.
پاسخ:
در صورت و مخرج عبارت فوق نیز توابع مثلثاتی داریم. ریشههای صورت و مخرج را جداگانه محاسبه میکنیم و سپس تعیین علامت میکنیم.
ابتدا ریشههای صورت را محاسبه میکنیم. همان طور که در قسمت مربوطه اشاره شد، ریشههای تابع تانژانت در بازه تعیین شده به صورت زیر است:
$$0,pm pi$$
اما ریشههای $$sec x$$ وجود ندارد. با این حال اگر کسر را در ابتدا ساده می کردیم حاصل آن $$sin x$$ بود و ریشههای آن به صورت زیر میشود:
$$sin x=pm npi$$
تعیین علامت $$sin x$$ در بازه $$-pi$$ تا $$+pi$$ به صورت زیر است:
$$boxed{begin{matrix}x & &-pi & & 0& & +pi& \sin x & + & 0 & – & 0 & + &0 & -\end{matrix}}$$

مثال پنجم تعیین علامت کسری
میخواهیم کسر $$y=frac{x^2-5x+6}{x^2-4}$$ را تعیین علامت کنیم.
پاسخ:
در صورت و مخرج کسر فوق چندجملهای درجه دوم داریم.
ابتدا ریشههای صورت را محاسبه میکنیم. در معادله درجه دوم چون دلتا مثبت و برابر 1 است بنابراین دارای دو ریشه حقیقی و متمایز زیر است:
$$x=2,3$$
سپس باید ریشههای معادله درجه دوم در مخرج را حساب کنیم.
$$x=pm2$$
اکنون که ریشههای صورت و مخرج را بدست آوردیم در جدول زیر تعیین علامت را انجام میدهیم.
$$boxed{begin{matrix}x & &-2 & & 2& & 3 & \ x^2-5x+6&+ &+ & + & 0&- & 0& +\ x^2-4& + & 0 & – &0 & +&+&+ \ y& + & infty& – &infty & -&0&+end{matrix}}$$
مثال ششم تعیین علامت کسری
عبارت $$y=frac{(2x-5)}{(x^2+4x+4)}$$ را تعیین علامت کنید.
پاسخ:
در صورت کسر یک عبارت چندجملهای درجه اول و در مخرج کسر یک چندجملهای درجه دوم داریم. ابتدا ریشههای صورت را حساب میکنیم.
$$2x-5=0 Rightarrow x=frac{5}{2}$$
سپس ریشههای مخرج را حساب میکنیم. با توجه به اینکه معادله درجه دوم است و دلتا برابر 0 است پس دو ریشه حقیقی ولی یکسان به صورت زیر داریم:
$$x=-2$$
با داشتن ریشههای صورت و مخرج در جدول زیر تعیین علامت را انجام میدهیم.
$$boxed{begin{matrix}x & & -2 & &5/2 & \ (2x-5)& – & – & – & 0 &+ \(x^2+4x+4) & + & 0 & + & + & + \ y&- & infty & – & 0 & +end{matrix}}$$
مثال هفتم تعیین علامت کسری
میخواهیم کسر $$y=frac{mid x-2mid}{x-3}$$ را تعیین علامت کنیم.
پاسخ:
در صورت این عبارت کسری یک قدرمطلق و در مخرج یک معادله درجه اول داریم. با تعیین ریشه صورت شروع میکنیم.
$$x=2$$
سپس ریشه مخرج را محاسبه میکنیم.
$$x=3$$
اکنون با داشتن ریشههای صورت و مخرج در جدول زیر تعیین علامت را انجام میدهیم.
$$boxed{begin{matrix}x & & 2 & & 3 & \ mid x-2mid& + & 0 & +&+ &+ \ x-3& – & – & – &0 & + \y & – &0 &- & infty & +end{matrix}}$$
مثال هشتم تعیین علامت کسری
عبارت $$y=frac{2mid x+1mid}{x-1}$$ را تعیین علامت کنید.
پاسخ:
در صورت این عبارت کسری یک قدرمطلق و در مخرج یک معادله درجه اول داریم. با تعیین ریشه صورت شروع میکنیم.
$$x=-1$$
سپس ریشه مخرج را محاسبه میکنیم.
$$x=1$$
حالا که ریشههای صورت و مخرج را داریم در جدول زیر تعیین علامت را انجام میدهیم.
$$boxed{begin{matrix}x & &-1 & & +1 & \2mid x+1mid & + & 0 & + & + & +\x-1 & – & – & – & 0 & +\y & – & 0 & – & infty & +end{matrix}}$$
مثال نهم تعیین علامت کسری
میخواهیم کسر $$y=frac{sin x}{log (x+1)}$$ را در بازه 0 تا $$+pi$$ تعیین علامت کنیم.
پاسخ:
در صورت کسر فوق یک تابع مثلثاتی و در مخرج کسر یک تابع لگاریتمی داریم. ریشه سینوس در بازه فوق به صورت زیر است:
$$sin x=+ npi$$
ریشه مخرج که شامل لگاریتم است به صورت زیر است:
$$x=0$$
بنابراین با داشتن ریشههای صورت و مخرج تعیین علامت را در جدول زیر انجام میدهیم.
$$boxed{begin{matrix}x & &0 & & pi\sin x & – & 0 & + & 0 & – \log (x+1) &- & 0 & + & + & + \y & + & infty & + & 0&-end{matrix}}$$
مثال دهم تعیین علامت کسری
میخواهیم کسر $$y=frac{log (x+1)}{x+6}$$ را تعیین علامت کنیم.
پاسخ:
در صورت کسر فوق یک تابع لگاریتمی و در مخرج آن یک تابع چندجملهای درجه اول داریم. ریشه لگاریتمی صورت کسر به صورت زیر است:
$$x=0$$
ریشه چندجملهای مخرج نیز به شکل زیر حساب کردیم:
$$x=-6$$
با داشتن ریشههای صورت و مخرج تعیین علامت را در جدول زیر انجام دادیم.
$$boxed{begin{matrix}x & &-6 & & 0\log (x+1) & – & – & – & 0 & + \x+6 &- & 0 & + & + & + \y & + & infty & – & 0&+end{matrix}}$$
ریشه انواع توابع
به زبان ساده هدف از تعیین علامت بررسی رفتار توابع در اطراف ریشههای آنها است. در عبارتهای کسری ممکن است انواع توابع وجود داشته باشند و تعیین علامت هرکدام از آن روش مخصوص خود را دارد. بنابراین ابتدا تعیین علامت هر یک از این توابع زا مورد بررسی قرار خواهیم داد.
تعیین علامت توابع چندجملهای
یک تابع چندجملهای درجه اول به شکل زیر است:
$$ax+b=0$$
در عبارت فوق $$x$$ متغیر و $$b$$ و $$a$$ ضریبهای ثابت هستند. برحسب مورد تابع چندجملهای میتواند پیچیدهتر شود. البته پیشتر در مجله فرادرس در مورد انواع تابع نیز توضیح دادهایم و میتوانید برای آشنایی بیشتر، آن را مطالعه کنید. برای تعیین ریشه توابع چندجملهای باید آن را مساوی صفر قرار داد و معادله را برحسب $$x$$ محاسبه کرد سپس میتوان این تابع را تعیین علامت کرد. در تعیین علامت به خاطر داشته باشید که مقادیر کمتر از ریشه معادله (سمت چپ نمودار) مخالف ضریب $$x$$ و مقادیر بیشتر از ریشه (سمت راست نمودار) موافق ضریب $$x$$ هستند. برای درک بهتر این موضوع به مثالهای زیر توجه کنید.
مثال اول تعیین علامت توابع چندجملهای
میخواهیم عبارت $$4x-2$$ را تعیین علامت کنیم.
پاسخ:
عبارت فوق یک چندجملهای درجه اول است و باید ابتدا ریشههای آن را مشخص کنیم.
$$4x-2=0Rightarrow x=frac{1}{2}$$
سپس مطابق توضیحات ذکر شده این عبارت را در جدول زیر تعیین علامت میکنیم.
$$boxed{begin{matrix}x & & & 1/2 & & \4x-2 & & – & 0 & + & \end{matrix}}$$
توابع قدرمطلق
یکی از توابع ساده و کاربردی در ریاضیات و مهندسی قدرمطلق است که به صورت زیر تعریف میشود:
$$|x| = begin{cases} x, & text{if } x geq 0 \ -x, & text{if } x < 0 end{cases}$$
که به زبان ساده هر مقدار مثبت یا منفی که وارد تابع قدر مطلق شود خروجی آن با علامت مثبت خواهد بود. تعیین علامت توابعی که قدرمطلق دارند بسیار آسان است زیرا علامت در اطراف ریشه همیشه مثبت است. به مثالهای زیر توجه کنید.
مثال اول تعیین علامت توابع قدرمطلق
عبارت $$mid x-2 mid$$ را تعیین علامت کنید.
پاسخ:
این عبارت یک تابع قدرمطلق است و ابتدا باید ریشه داخل قدرمطلق را حساب کنیم.
$$x-2=0 Rightarrow x=2$$
اکنون با داشتن ریشه عبارت قدرمطلق آن را در جدول زیر تعیین علامت میکنیم.
$$boxed{begin{matrix}x & & & 2 & & \mid x-2 mid & & + & 0 & + & \end{matrix}}$$
توابع نمایی و لگاریتمی
شکل ساده توابع نمایی به صورت زیر است:
$$y=a^x$$
در عبارت فوق $$a$$ عدد ثابت و $$x$$ متغیر است. اگر $$a$$ مثبت باشد آنگاه علامت تابع مثبت خواهد شد و اگر $$a$$ منفی باشد علامت تابع منفی میشود. به مثالهای زیر توجه کنید.
مثال اول تعیین علامت توابع نمایی
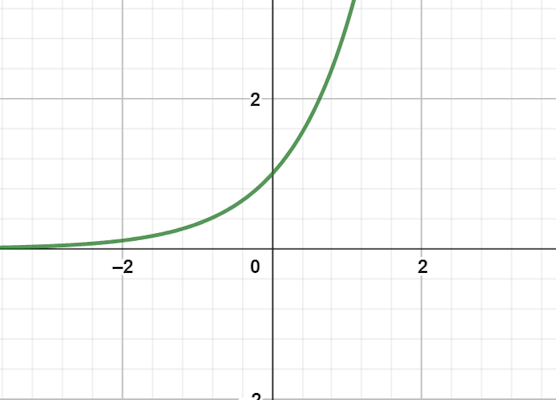
میخواهیم تابع نمایی $$y=3^x$$ را تعیین علامت کنیم.
پاسخ:
همانطور که در شکل زیر مشخص است، تابع نمایی فاقد ریشه است ولی علامت آن در تمام نقاط مثبت است.
شکل ساده توابع لگاریتمی به صورت زیر است:
$$y=log_{a}{x}$$
در عبارت فوق a عدد ثابت و مبنای لگاریتم نامیده میشود که همیشه مثبت است همچنین $$x$$ متغیر است. تعیین علامت لگاریتم به علامت $$x$$ بستگی دارد.
- اگر $$x>0$$ باشد آنگاه
-
- کمتر از ریشه $$Leftarrow$$ علامت منفی
- بیشتر از ریشه $$Leftarrow$$ علامت مثبت
- اگر $$x<0$$ باشد آنگاه
-
- کمتر از ریشه $$Leftarrow$$ علامت مثبت
- بیشتر از ریشه $$Leftarrow$$ علامت منفی
نکته: $$lnx$$ نیز لگاریتم در مبنای e است و از همین روال پیروی میکند. برای درک بهتر به مثالهای زیر توجه کنید.
مثال اول تعیین علامت توابع لگاریتمی
میخواهیم عبارت $$log (3x-1)$$ را تعیین علامت کنیم.
پاسخ:
عبارت فوق یک تابع لگاریتمی است که ابتدا باید ریشه آن را محاسبه کنیم.
$$log (3x-1) =0$$
از آنجا که این لگاریتم در مبنای ۱۰ است رابطه فوق را بازنویسی میکنیم.
$$ (3x-1) =10^0=1$$
سپس معادله را برحسب $$x$$ حل میکنیم.
$$ 3x=1+1=2$$
$$x=frac{2}{3}$$
اکنون با داشتن ریشه عبارت لگاریتمی و با استفاده از توضیحات فوق مطابق جدول زیر تعیین علامت میکنیم.
$$boxed{begin{matrix}x & & & 2/3 & & \log (3x-1) & & – & 0 & + & \end{matrix}}$$
توابع درجه دوم
شکل کلی معادله درجه دوم به صورت زیر است:
$$ax^{2}+bx+c=0$$
که عوامل به کار رفته به شرح زیر هست:
- x: متغیر معادله
- b، a و c: ضرایب متغیر معادله
شکل معادله درجه دوم به صورت یک منحنی است و این بخاطر وجود $$x^{2}$$ میتواند باشد. اگر در معادله فوق $$a=0$$ باشد آنگاه معادله به درجه یک تبدیل میشود. همانطور که میدانید روش حل عمومی معادله درجه دوم، روش دلتا نام دارد که به صورت زیر است:
$$x=frac{-bpm sqrt{triangle}}{2a}$$
و در این معادله دلتا ($$triangle$$) به صورت زیر تعریف میکنیم:
$$b^{2}-4ac$$
جوابهای معادله به علامت دلتا بستگی دارد.
دلتا بزرگتر از صفر
اگر دلتا بزرگتر از صفر باشد پس معادله دو ریشه حقیقی و متمایز دارد. با توجه به جدول زیر اگر $$x_1$$ و $$x_2$$ جوابهای معادله باشند، علامت در محدوده آنها همیشه مخالف علامت $$a$$ خواهد بود و علامت خارج از محدوده آنها موافق $$a$$ خواهد بود. برای درک بهتر این موضوع به شکل زیر توجه کنید.
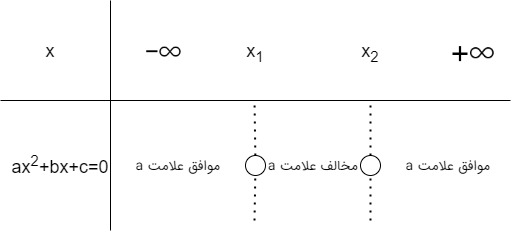
دلتا برابر صفر
اگر دلتا برابر صفر بود پس معادله ریشههای حقیقی و یکسان دارد و علامت معادله بیشتر یا کمتر از ریشه معادله ($$x_1$$) همواره موافق علامت $$a$$ خواهد بود. برای درک بهتر به شکل زیر توجه کنید.
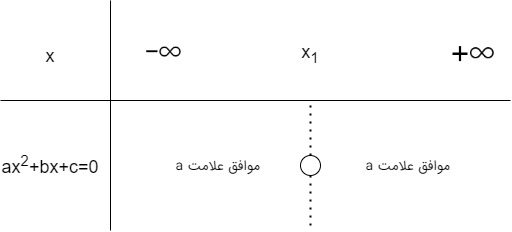
دلتا کوچکتر از صفر
اگر دلتا کوچکتر از صفر بود پس معادله ریشه حقیقی ندارد بنابراین علامت معادله همواره موافق علامت a خواهد بود.
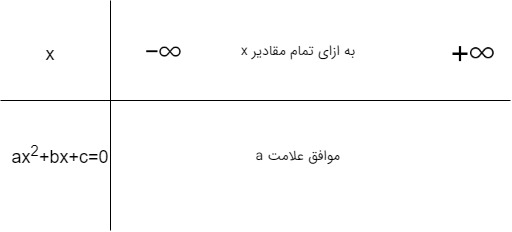
به مثالهای زیر توجه کنید.
مثال اول تعیین علامت توابع درجه دوم
میخواهیم عبارت $$x^2-4x+4=y$$ را تعیین علامت کنیم.
پاسخ:
این یک معادله درجه دوم است که باید ابتدا دلتای آن را محاسبه کرد.
$$triangle={b^{2}-4ac}$$
$$triangle=0$$
با توجه به اینکه دلتا صفر شد پس معادله دارای دو ریشه حقیقی و یکسان به صورت زیر است.
$$x=2$$
حال با داشتن ریشه معادله فوق میتوانیم تعیین علامت را مطابق جدول زیر انجام دهیم.
$$boxed{begin{matrix}x & & & 2 & & \x^2-4x+4 & & + & 0 & + & \end{matrix}}$$
مثال دوم تعیین علامت توابع درجه دوم
عبارت $$2x^2-5x+2=y$$ را تعیین علامت کنید.
پاسخ:
این یک معادله درجه دوم است که باید ابتدا دلتای آن را محاسبه کرد.
$$triangle={b^{2}-4ac}$$
$$triangle=9$$
با توجه به اینکه دلتا مثبت شد پس معادله دارای دو ریشه حقیقی و متمایز به صورت زیر است.
$$x=frac{1}{2}$$
$$x=2$$
اکنون با داشتن ریشههای معادله فوق میتوانیم تعیین علامت را طبق جدول زیر انجام دهیم.
$$boxed{begin{matrix}x& & 1/2 & & 2 & & \2x^2-5x+2 &+& 0 & – & 0 & + & \end{matrix}}$$
مثال سوم تعیین علامت توابع درجه دوم
میخواهیم عبارت $$3x^2+2x+1=y$$ را تعیین علامت کنیم.
پاسخ:
این یک معادله درجه دوم است که باید ابتدا دلتای آن را محاسبه کرد.
$$triangle={b^{2}-4ac}$$
$$triangle=-8$$
با توجه به اینکه دلتا منفی شد پس معادله دارای ریشه حقیقی نیست و به صورت زیر تعیین علامت میشود. توجه کنید که در زیر عبارت (any x) به معنی به ازای هر مقدار از $$x$$ است.
$$boxed{begin{matrix}x& & & & any &x & & \3x^2+2x+1 && & & + & & \end{matrix}}$$

توابع مثلثاتی
تعیین علامت توابع مثلثاتی کمی پیچیدهتر است چون هرکدام از آنها رفتار متفاوتی دارد که در زیر هر یک را توضیح میدهیم.
توابع سینوس
ریشههای $$sin(x)$$ به صورت زیر است:
$$0,pmpi,pm2pi,…$$
برای تعیین علامت از آن به شکل زیر عمل میکنیم:
-
- مقادیر کمتر از ریشه علامت مثبت
- مقادیر بیشتر از ریشه علامت منفی
- مضارب زوج سینوس
-
- مقادیر کمتر از ریشه علامت منفی
- مقادیر بیشتر از ریشه علامت مثبت
توابع کسینوس
ریشههای $$cos(x)$$ به صورت زیر است:
$$pm frac{pi}{2},pmfrac{3pi}{2},pmfrac{5pi}{2},…$$
که رابطه عمومی کسینوس برای ریشههای آن به شکل زیر است:
$$(2n+1)timesfrac{pi}{2}$$
برای تعیین علامت از آن به شکل زیر عمل میکنیم:
- اگر n فرد باشد:
-
- مقادیر کمتر از ریشه علامت مثبت
- مقادیر بیشتر از ریشه علامت منفی
- اگر n زوج باشد:
-
- مقادیر کمتر از ریشه علامت منفی
- مقادیر بیشتر از ریشه علامت مثبت
توابع تانژانت
ریشههای $$tan(x)$$ به صورت زیر است:
$$0,pm pi, pm2pi,…$$
برای تعیین علامت از تانژانت به شکل زیر عمل میکنیم:
- مقادیر کمتر از ریشه علامت منفی
- مقادیر بیشتر از ریشه علامت مثبت
توابع کوتانژانت
ریشههای $$cot(x)$$ به صورت زیر است:
$$pmfrac{pi}{2},pmfrac{3pi}{2},…$$
برای تعیین علامت از کوتانژانت به شکل زیر عمل میکنیم:
- مقادیر کمتر از ریشه علامت مثبت
- مقادیر بیشتر از ریشه علامت منفی
نکته: توابع $$sec x$$ و $$csc x$$ ریشه ندارند و باید با استفاده از روابط مثلثاتی در صورت لزوم آنها را به دیگر توابع مثلثاتی تبدیل کنید.
برای فهم بیشتر به مثالهای زیر توجه کنید:
مثال اول تعیین علامت توابع مثلثاتی
میخواهیم عبارت $$sin (2x-2)$$ را تعیین علامت کنیم.
پاسخ:
این عبارت یک تابع مثلثاتی است که برای محاسبه ریشه آن باید تابع را مساوی صفر قرار داد.
$$sin (2x-2)=0$$
با استفاده از توضیحات فوق میدانیم که تابع سینوس در نقاط $$n pi$$ صفر میشود، بنابراین:
$$ (2x-2)=n pi$$
$$ 2x=n pi+2$$
درنتیجه ریشههای معادله به صورت زیر خواهد بود:
$$ x=frac{n pi}{2}+1$$
در این مثال تابع را در بازه ۰ تا $$pi$$ بررسی میکنیم.
اکنون با داشتن ریشه معادله میتوانیم طبق جدول زیر عبارت را تعیین علامت کنیم.
$$boxed{begin{matrix}x & & 1 & & frac{pi}{2}+1 & \sin (2x-2) & -& 0 & + & 0 & – \end{matrix}}$$
مثال دوم تعیین علامت توابع مثلثاتی
میخواهیم عبارت $$cos (x-4)$$ را تعیین علامت کنیم.
پاسخ:
این عبارت یک تابع مثلثاتی است که برای محاسبه ریشه آن باید تابع را مساوی صفر قرار داد.
$$(x-4)=0$$
همانطور که در قسمت قبل اشاره شد تابع کسینوس در نقاط $$(2n+1)timesfrac{pi}{2}$$ صفر میشود، پس خواهیم داشت:
$$x-4=(2n+1)timesfrac{pi}{2}$$
بنابراین ریشههای معادله به صورت زیر خواهد بود:
$$x=(2n+1)timesfrac{pi}{2}+4$$
در این مثال تابع را در بازه ۰ تا $$ pi$$ بررسی میکنیم.
اکنون با داشتن ریشه معادله میتوانیم طبق جدول زیر عبارت را تعیین علامت کنیم.
$$boxed{begin{matrix}x & & frac{-pi-8}{2} & \cos (x-4) & – & 0 & + \end{matrix}}$$
مثال سوم تعیین علامت توابع مثلثاتی
میخواهیم عبارت $$tan (2x+5)$$ را تعیین علامت کنیم.
پاسخ:
این عبارت یک تابع مثلثاتی است که برای محاسبه ریشه آن باید تابع را مساوی صفر قرار داد.
$$tan (2x+5)=0$$
با استفاده از توضیحات فوق میدانیم که تابع سینوس در نقاط $$n pi$$ صفر میشود، بنابراین:
$$ (2x+5)=npi$$
$$ 2x=npi-5$$
درنتیجه ریشههای معادله به صورت زیر خواهد بود:
$$ x=frac{npi}{2}-frac{5}{2}$$
در این مثال تابع را در بازه ۰ تا $$frac{pi}{2}$$ بررسی میکنیم.
اکنون با داشتن ریشه معادله میتوانیم طبق جدول زیر عبارت را تعیین علامت کنیم.
$$boxed{begin{matrix}x & & frac{2pi-5}{2} & \tan (2x+5) & -& 0 & + \end{matrix}}$$
توابع جز صحیح
شکل کلی توابع جز صحیح به صورت زیر است:
$$y=[x]$$
تابع جز صحیح، تابعی با خروجیهای صحیح است. این تابع ورودی دلخواه (حقیقی) را به کوچکترین عدد صحیح مجاور تبدیل میکند. برای تعیین علامت تابع جز صحیح نیاز است تا حدود ورودی تعیین شود. بنابر محدود تعیین شده، علامت تابع جز صحیح میتواند صفر، مثبت یا منفی باشد. به مثال زیر توجه کنید
مثال اول تعیین علامت توابع جز صحیح
میخواهیم تابع $$y=[frac{1}{2}x]$$ را در بازههای (1,0-] و (0,1] و (1,2] بررسی کنیم.

پاسخ:
همانطور که قبلا توضیح داده شد، تابع جز صحیح با توجه به بازه تعیین شده میتواند علامت متفاوت داشته باشد. در ستون سمت چپ جدول زیر تابع بین بازههای تعریف شده قرار گرفته است و در ستون وسط مقدار تابع پس از محاسبه جز صحیح است که از تعریف جز صحیح استفاده کردیم و در ستون سمت راست نیز علامت تابع قرار دارد.
| تعیین علامت تابع | مقدار x پس از محاسبه جز صحیح | تابع در بازه تعریف شده |
| 1- | $$-2 le x <0$$ | $$-1 le frac{1}{2}x <0$$ |
| 0 | $$0 le x <2$$ | $$0 le frac{1}{2}x <1$$ |
| 1+ | $$2 le x <4$$ | $$1 le frac{1}{2}x <2$$ |
توابع رادیکالی
شکل ساده توابع رادیکالی به صورت زیر است:
$$y=sqrt{x}$$
علامت توابعی که زیر رادیکال هستند همواره مثبت است. به مثالهای زیر توجه کنید.
مثال اول تعیین علامت توابع رادیکالی
عبارت $$sqrt{4x-6}$$ را تعیین علامت کنید.
پاسخ:
این عبارت یک تابع رادیکالی است که برای محاسبه ریشه آن باید تابع را مساوی صفر قرار داد.
$$4x-6=0$$
ریشه این تابع به صورت زیر است.
$$x=frac{3}{2}$$
چون تابع رادیکالی است بنابراین رفتار تابع در اطراف ریشه مثبت است.
$$boxed{begin{matrix}x & & frac{3}{2} & \sqrt{4x-6} & + & 0 & + \end{matrix}}$$
نتیجهگیری
با استفاده از تکنیک تعیین علامت میتوانیم رفتار تابع را در اطراف ریشههایش بررسی کنیم. تعیین علامت عبارت کسری میتواند شامل انواع توابع مانند مثلثاتی، درجه دوم، نمایی، لگاریتمی و غیره باشد که در این مطلب از مجله فرادرس با انواع مثالهای متنوع مورد بررسی قرار دادیم. برای تعیین علامت عبارتهای کسری باید ریشههای صورت و مخرج را محاسبه کنیم و مطابق آنچه که در این مطلب آموزش داده شد کل عبارت کسری را تعیین علامت کنیم.
source