الگوریتم‌های بهینه‌سازی از دسته الگوریتم‌هایی به شمار می‌آیند که به منظور یافتن بهترین راه‌حل ممکن برای مسئله‌ای خاص مورد استفاده قرار می‌گیرند. هدف اصلی این الگوریتم‌ها یافتن راه‌حل بهینه است که با توجه به نوع مسئله مورد نظر، تابع هدف مرتبط با آن، کمینه یا بیشینه می‌شود. این توابع هدف معمولاً به عنوان معیاری برای اندازه‌گیری کیفیت یا عملکرد راه‌حل‌های پیشنهادی عمل می‌کنند. ما در این مطلب از مجله فرادرس یاد می‌گیریم که الگوریتم بهینه سازی چیست و انواع الگوریتم بهینه‌سازی را تعریف می‌کنیم. همچنین، در قسمتی از مطلب به انواع مسائل بهینه‌سازی به همراه چند نمونه مثال در کاربردهای واقعی می‌پردازیم. در نهایت، چند الگوریتم پرکاربرد در مسائل بهینه‌سازی را به اختصار شرح می‌دهیم.

الگوریتم بهینه سازی چیست؟

در این بخش از مطلب، به این موضوع می‌پردازیم که الگوریتم بهینه سازی چیست و تعریف مسئله بهینه‌سازی و کاربردهای آن را بررسی می‌کنیم.الگوریتم‌های بهینه‌سازی می‌توانند به عنوان الگوریتم‌هایی توصیف شوند که سعی می‌کنند هنگام ارائه مجموعه‌ای از شرایط یا محدودیت‌ها بهترین راه‌حل را پیدا کنند. این الگوریتم‌ها ابزارهای قدرتمندی هستند که برای حل مسائل بهینه سازی استفاده می‌شوند و در زمینه‌های مختلفی مانند مهندسی و تحقیق عملیات مورد استفاده قرار می‌گیرند.

انتخاب نوع الگوریتمی که استفاده می‌شود به ماهیت مسئله‌ای که حل می‌شود بستگی دارد. بهینه‌سازی به معنای یافتن مقداری مناسب برای مجموعه‌ای از پارامترها یا متغیرهای تابع هدف است، به گونه‌ای که این مقادیر منجر به حداکثر یا حداقل شدن ارزیابی تابعی شوند. همانطور که گفتیم الگوریتم‌های بهینه‌سازی ابزاری برای حل مسائل بهینه‌‌سازی هستند. اکنون، به تعریف مسئله بهینه‌سازی، کاربردها و انواع آن‌ می‌پردازیم.

مسئله بهینه‌ سازی

در ریاضیات، مهندسی، علوم کامپیوتر و اقتصاد، یک مسئله بهینه‌سازی، مسئله یافتن بهترین راه‌حل از میان تمامی راه‌حل‌های ممکن است. برای انتخاب الگوریتم بهینه‌سازی مناسب به منظور حل مسئله بهینه‌سازی، دانستن نوع مسئله بهینه‌سازی اهمیت زیادی دارد. مسائل بهینه‌سازی در دنیای واقعی بسیار متنوع هستند. در ادامه، به برخی از مسائل بهینه‌سازی در دنیای واقعی اشاره می‌شود.

مثال هایی از مسائل بهینه‌ سازی

تا اینجا، یاد گرفتیم که الگوریتم بهینه سازی چیست و به تعریف مسئله بهینه سازی پرداختیم. حال، با برخی از مثال‌های الگوریتم‌های بهینه‌سازی آشنا می‌شویم.

• «مسئله فروشنده دوره‌گرد» ( Travelling Salesman Problem |TSP): مسئله TSP مسئله بهینه‌سازی ریاضی است که در آن یک فروشنده باید کوتاه‌ترین مسیر را برای بازدید از مجموعه‌ای از شهرها و بازگشت به نقطه شروع پیدا کند. این مسئله در کاربردهای مختلفی مانند برنامه‌ریزی مسیر، طراحی شبکه، و تخصیص منابع کاربرد دارد.
• مسئله معروف رژیم غذایی: این مسئله، از مسائل بهینه‌سازی خطی به شمار می‌آید که در آن دستوری برای وعده غذایی مغذی و کافی و تا حد امکان ارزان برای افراد تهیه می‌شود.
• تخصیص بهینه دارایی‌ها در سبد سرمایه‌گذاری: هدف از تخصیص بهینه دارایی‌ها، ایجاد یک سبد سرمایه‌گذاری متعادل است که هم ریسک و هم بازدهی مناسبی را ارائه دهد. این کار با در نظر گرفتن عوامل مختلفی مانند میزان ریسک‌پذیری سرمایه‌گذار، انتظارات بازده، و ویژگی‌های مختلف دارایی‌ها انجام می‌شود.
• «سیستم‌های توصیه‌گر» (Recommender Systems): در سال ۲۰۰۶ رقابتی بزرگ توسط شرکت «نتفلیکس» (Netflix) برگزار شد و هدف آن، افزایش دقت سیستم پیشنهاد فیلم بر اساس سلیقه کاربران بود. شرکت‌کنندگان از سراسر جهان به این چالش دعوت شدند تا تابع «رتبه‌بندی» (Ranking function) را توسعه دهند که بتواند بهبود ۱۰ درصدی در دقت سیستم پیشنهاد فیلم نتفلیکس ایجاد کند. در سال ۲۰۰۹، تیمی موفق به کسب جایزه و باعث بهبود دقت سیستم پیشنهاد فیلم نتفلیکس شد. این رقابت یکی از معروف‌ترین و پیچیده‌ترین رقابت‌های چالش‌برانگیز در زمینه یادگیری ماشین بود.
• «قطعه‌بندی تصویر» (Image Sgmentation): قطعه‌بندی تصاویر از مسائل حوزه بینایی ماشین است که شامل تقسیم تصویر به نواحی معنادار مانند اشیا، پس‌زمینه یا بافت‌ها است. این مسئله در موارد مختلفی مانند تشخیص شی، شناسایی چهره یا تصویربرداری پزشکی کاربرد دارد.

انواع مسائل بهینه سازی

گامی مهم برای انتخاب الگوریتم بهینه‌سازی مناسب برای هر مسئله، طبقه‌بندی نوع مسئله است، زیرا، هر الگوریتم‌ بهینه‌سازی برای حل دسته خاصی از مسائل بهینه‌سازی طراحی شده‌ است. در این قسمت، انواع برخی از طبقه‌بندی‌های مهم در مسائل بهینه‌سازی را مطرح می‌کنیم.

مسائل بهینه سازی بدون محدودیت

در مسائل بهینه‌سازی بدون محدودیت، قیدی بر روی متغیرها تعریف نمی‌شود. هدف این دسته از مسائل کمینه‌سازی تابع هدفی است که متغیر‌هایش می‌تواند بر روی مقادیر حقیقی تعریف شوند. مسائل بهینه‌سازی بدون محدودیت گاهی مستقیما به عنوان مسئله‌ای کاربردی مطرح می‌شود. اما در برخی مواقع پس از فرموله‌بندی مجدد مسئله بهینه‌سازی با محدودیت، ایجاد می‌شود. به این ترتیب، با تعیین جریمه برای نقض قیدها، مسئله را به یک مسئله بهینه‌سازی بدون محدودیت می‌توانیم تبدیل کنیم. این روش به افراد امکان می‌دهد که از الگوریتم‌های بهینه‌سازی بدون محدودیت برای حل مسائل بهینه‌سازی با محدودیت استفاده کنند.

مسائل بهینه‌سازی با محدودیت

مسائل بهینه‌سازی با محدودیت، در کابردهایی ایجاد می‌شوند که شروطی به طور صریح بر روی متغیرهای مسئله اعمال می‌شوند. به عنوان مثال، یک متغیر، ممکن است ملزم به قرارگیری در بازه‌ای تعیین شده باشد یا اینکه به جای اِعمال قیدها به طور خاص بر روی یک متغیر، با استفاده از تعیین روابط بین چند متغیر یا استفاده از معادلات پیچیده‌، این محدودیت‌ها به مسئله اِعمال شوند. به طور خلاصه، مشکلات بهینه سازی بدون قید، حل ساده تری دارند، در حالی که مشکلات با قید واقع بینانه‌ترند و محدودیت‌های واقعی را در نظر می‌گیرند. مسائل بهینه‌سازی با محدودیت را بر اساس ماهیت محدودیت‌ها می‌توان به زیر دسته مسئله‌های خطی، غیر خطی، محدب، مشتق‌‌پذیر یا غیر‌ مشتق‌پذیر تقسیم کرد.

مسائل بهینه سازی قطعی

در بهینه‌سازی قطعی، فرض بر این است که داده‌های مسئله به طور دقیق شناسایی و تمامی توابع هدف و قیدها به صورت صریح و معین تعریف شده‌اند. با این حال، برای بسیاری از مسائل دنیای واقعی، داده‌ها به دلایل مختلف نمی‌توانند به طور دقیق شناخته شوند که این امر می‌تواند به دلیل خطای اندازه‌گیری یا مرتبط بودن داده‌ها به زمان آینده باشد.در اینصورت، به سادگی نمی‌توان آن‌ها را قطعی دانست. لازم به ذکز است که، مسائل بهینه‌سازی قطعی نسبت به مسائل بهینه‌سازی غیر قطعی آسان‌تر است.

مسائل بهینه سازی غیر قطعی

در این نوع مسائل، ما با عدم قطعیت در داده‌ها یا پارامترهای مدل روبرو هستیم و می‌خواهیم یک راه‌حل بهینه برای مدل در شرایط عدم قطعیت پیدا کنیم. مدل‌های بهینه‌سازی غیرقطعی بر این اصل تکیه دارند که توزیع‌ احتمال حاکم بر داده‌ها قابل شناسایی یا تخمین هستند. پس در این نوع مسائل هدف یافتن روشی است که برای همه یا بخش قابل توجهی از داده‌های مسئله قابل اجرا باشد و عملکرد مورد انتظار مدل را بهینه کند.

انواع الگوریتم های بهینه سازی

تا این قسمت از مطلب، یاد گرفتیم که الگوریتم بهینه سازی چیست و اشاره‌ای به چند کاربرد آن در دنیای واقعی کردیم. در ادامه، به این نکته اشاره داشتیم که برای انتخاب الگوریتم بهینه‌سازی مناسب نیاز است که نوع مسئله بهینه‌سازی را شناسایی کنیم.

این امر، راهنمای خوبی برای انتخاب الگوریتم بهینه‌سازی مناسب برای مسئله‌مان است. در این قسمت از مطلب، به یکی از دسته‌بندی‌های متداول الگوریتم‌های بهینه‌سازی می‌پردازیم.

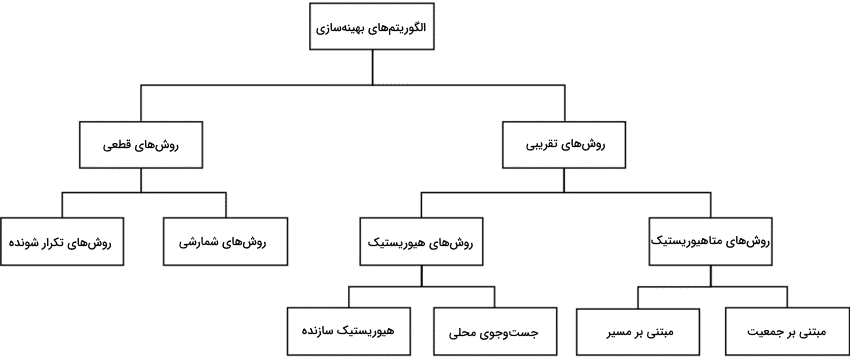
الگوریتم‌های بهینه‌سازی را می‌توان بر اساس رویکردهای آن‌ها به انواع مختلفی طبقه‌بندی کرد. تصویر بالا یکی از طبقه‌بندی‌های معمول الگوریتم‌های بهینه‌سازی را نمایش می‌دهد. در ادامه مطلب، هر یک از این‌ روش‌ها و الگوریتم‌ها توضیح می‌دهیم.

بهینه سازی قطعی

الگوریتم‌های «بهینه‌سازی قطعی» (Deterministic Optimization) به صورت تئوری تضمین می‌کنند که بهترین راه‌حل را برای مسائل بهینه‌سازی پیدا می‌کنند. روش‌های بهینه‌سازی قطعی معمولاً زمانی استفاده می‌شوند که یافتن راه‌حل بهینه در کل دامنه ورودی- یا به عبارت دیگر، یافتن بهینه سراسری – در مسئله مورد نظر، ضرورت داشته باشد. با این وجود، الگوریتم‌های بهینه‌سازی قطعی ممکن است در مسائلی با فضاهای جست‌وجوی بزرگ و پیچید کارایی نداشته باشند و زمان اجرا بسیار طولانی شود. این الگوریتم‌ها شامل روش‌های تکرار شونده و شمارشی هستند که به اختصار به آن‌ها می‌پردازیم.

روش های تکرار شونده

رویکرد برخی از الگوریتم‌های بهینه‌‌سازی به این صورت است که از نقطه‌ای تصادفی شروع می‌کنند و در هر مرحله تصمیم می‌گیرند که چه قدمی بردارند تا به نقطه بیشینه یا کمینه تابع هدف نزدیک شوند. به عبارتی دیگر، در این نوع روش‌ها یک راه‌حل اولیه انتخاب می‌شود و سپس با تکرار دنباله‌ای از مراحل، به سمت راه‌حل بهینه حرکت می‌کنند. روش‌های تکراری معمولاً در مسائل بهینه‌سازی استفاده می‌شوند که به دنبال راه‌حل‌های دقیق می‌گردند.

برای مثال، تصور کنید ما می‌خواهیم از نقطه‌ مشخصی از شهر به مرکز شهر بریم، اما مسیر را نمی‌دانیم و همچنین GPS غیرفعال است. بنابراین، می‌بایست از افراد در مسیر سوالاتی کنیم تا به مقصد برسیم. به عبارت دیگر، با پرسش از افراد در طول مسیر، در نهایت به مقصد مورد نظر خواهیم رسید. مثالی از روش بهینه‌سازی تکرار شونده، روش «گرادیان کاهشی» (Gradient Descent) است. در این روش، ابتدا راه‌حلی اولیه انتخاب می‌شود و سپس متغیرها در جهت گرادیان تابع هدف حرکت می‌کند. گرادیان تابع هدف، جهتی است که در آن مقدار تابع هدف بیشترین شیب را دارد. این حرکت تا زمانی ادامه می‌یابد که به نقطه‌ای برسیم که گرادیان صفر شود.

روش های شمارشی

روش‌های‌ شمارشی برای حل مسائل «بهینه‌سازی ترکیبی» (combinatorial optimization) استفاده می‌شود و از روش‌های بهینه‌سازی دقیق هستند که کل فضای راه‌حل را بررسی و ارزیابی می‌کنند تا راه‌حل بهینه را پیدا کنند. این روش‌ها زمانی به کار می‌روند که فضای راه‌حل گسسته و محدود است، یکی از ویژگی‌های اصلی روش‌های بهینه‌سازی شمارشی این است که آن‌ها همه ترکیب‌های ممکن از راه‌حل‌های امکان‌پذیر را در نظر می‌گیرند و هدف یافتن ترکیبی است که تابع هدف را بهینه می‌کند.

بهینه سازی تقریبی

تا این بخش از مطلب، یاد گرفتیم که روش‌های قطعی در الگوریتم بهینه سازی چیست، حال، به الگوریتم‌های تقریبی می‌پردازیم. الگوریتم‌های بهینه‌سازی «تقریبی» (Stochastic) به دنبال یافتن راه‌حل‌های تقریبا بهینه برای حل مسائل بهینه‌سازی هستند. این رو‌ش‌ها بیشتر در مواردی مورد استفاده قرار می‌گیرند که یافتن دقیق راه‌حل بهینه از نظر محاسباتی غیر ممکن یا زمان‌بر است. بنابراین، این دسته از الگوریتم‌ها راه‌حل‌هایی را ارائه می‌دهند که نزدیک به بهترین راه‌حل ممکن هستند اما لزوما بهترین نیستند. روش‌های بهینه‌سازی «هیوریستیک» (Heuristic) و «متاهیوریستیک» (Meta Heuristic) از روش‌های تقریبی حل مسائل بهینه‌سازی به شمار می‌آیند. برخی از نمونه‌ الگوریتم‌های بهینه‌سازی تقریبی شامل «جست‌وجوی حریصانه» ( Greedy Search)، «جست‌وجوی تابو» (Tabu Search) و الگوریتم‌های تکاملی هستند.

روش های هیوریستیک

الگوریتم‌های هیوریستیک سعی دارند نسبت به الگوریتم‌های دقیق، سریع‌تر عمل و از رویکردهای سریع‌تری برای حل مسائل پیچیده‌ استفاده کنند. اصطلاح «هیوریستیک» (Heuristic) در زبان انگلیسی به معنای «کشف کردن» است. این دسته از الگوریتم‌ها سعی در کشف راه‌حلی تقریبی برای یافتن پاسخی مورد قبول در زمانی معقول برای مسئله بهینه‌سازی دارند. بنابراین، این الگوریتم‌ها راه‌حلی برای حلی مسئله بهینه‌سازی مشخص، ارائه می‌دهند که لزوما راه‌حل بهینه نیست، بلکه، راه‌حلی به اندازه کافی خوب است. الگوریتم جست‌و‌جوی حریصانه نمونه‌ای از الگوریتم‌های هیوریستیک به شمار می‌آید.

در برخی مواقع‌، از الگوریتم‌های بهینه‌سازی هیوریستیک نه‌تنها برای یافتن نتیجه، بلکه برای حذف برخی نتایج نادرست، استفاده می‌شود. در چنین حالتی بخش‌هایی از فضای جست‌وجوی مسئله توسط این الگوریتم‌ها حذف می‌شوند و باقی‌مانده فضای جست‌وجو با استفاده از روشی دیگر، مورد بررسی قرار می‌گیرد. این الگوریتم‌ها «هیوریستیک پشتیبان» (supporting heuristics) نامیده می‌شوند. تصویر زیر، مثالی از مسئله TSP را نمایش می‌دهد که با استفاده از ۳ روش «بروت فورس» (Bruteforce)، «هیوریستیک پشتیبان» (Supporting Heuristics) و روش «حریصانه‌» (Greedy) حل شده است.

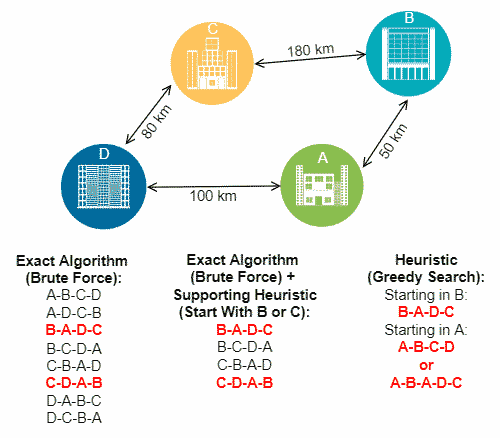
در تصویر بالا نتایج نهایی قرمز‌رنگ است. می‌توان ملاحظه کرد که الگوریتم‌های قطعی – که برای مثال، در اینجا الگوریتم «بروت فورس» (‌Brute Force) مورد استفاده قرار گرفته است – بهینه سراسری را پیدا کرده است. همچنین، استفاده از الگوریتم دقیق بروت فورس به‌همراه هیوریستیک پشتیبان نیز، منجر به یافتن بهینه سراسری شده است. در انتها، می‌توان مشاهده کرد که الگوریتم بهینه‌سازی هیوریستیک نظیر جست‌وجوی حریصانه، به بهینه سراسری منجر نشده است. اما، پاسخی نزدیک به راه‌حل بهینه را پیدا کرده است. در ادامه به انواع الگوریتم‌های هیوریستیک می‌پردازیم.

• «هیوریستیک سازنده» (Constructive Heuristic): هیوریستیک سازنده به جای حل کل مسئله در یک مرحله، مسئله را به چندین زیرمسئله تقسیم می‌کند. سپس هر یک از این زیرمسائل را به صورت جداگانه حل کرده و نتایج جزئی را با هم ترکیب می‌کند تا به یک نتیجه کلی برسد. این روش زمانی مورد استفاده قرار می‌گیرد که حل کل مسئله به صورت مستقیم با مشکل مواجه شود. این روش‌ها به صورت مکرر راه‌حل فعلی را گسترش می‌دهند تا زمانی که راه‌حل کامل شود. «مسیریابی وسیله نقلیه» (VRP| vehicle routing problem) و «زمانبندی گردش کاری کارگاه» (flow shop scheduling problem |BFSP) از مسائل معروفی هستند که با استفاده از الگوریتم‌های هیوریستیک سازنده قابل حل هستند.
• «جست‌ و جوی محلی» (Local Search): الگوریتم جست‌وجوی محلی یک نقطه را به صورت تصادفی به عنوان راه‌حل اولیه انتخاب می‌کند. سپس، در هر مرحله با اعمال تغییراتی جزئی به راه‌حل مرحله قبل، سعی در بهبود آن راه‌حل شده دارد. به این منظور، یک رابطه همسایگی در فضای جستجو تعریف شود و در هر مرحله، الگوریتم در راه‌حل‌های همسایه حرکت می‌کند تا به حل بهینه یا حل قابل قبولی برسد.

روش‌‌های متاهیوریستیک

مشابه الگوریتم‌های بهینه‌سازی هیوریستیک الگوریتم‌های «متاهیوریستیک» (Meta Heuristic) به دنبال یافتن پاسخی مورد قبول و نزدیک به بهینه برای مسئله هستند. اما، الگوریتم هیوریستیک به طور عمده برای حل مسئله‌ای معین طراحی می‌شود و عملکرد خود را بر اساس ویژگی‌های مسئله‌ای خاص بهبود می‌دهد. اما، الگوریتم‌های متاهیوریستیک به صورت عمومی‌تر و مستقل از جزئیات خاص مسئله طراحی می‌شوند.

در واقع، اصلی‌ترین تفاوت بین الگوریتم‌های هیوریستیک و الگوریتم‌های متاهیوریستیک در این است که الگوریتم متاهیوریستیک به طور مستقیم بر اساس ویژگی‌های مسئله طراحی می‌شود، در حالی که، الگوریتم‌های متاهیوریستیک مستقل از مسئله هستند و و تنها با تنظیم برخی پارامترها قابلیت حا تعداد زیادی از مسائل بهینه‌سازی را دارند. اکنون، با توجه به نحوه عملکرد الگوریتم‌های متاهیوریستیک، می‌توان این روش‌ها را به ۲ دسته کلی تقسیم کرد.

• مبتنی بر مسیر: یکی از ویژگی‌های اصلی الگوریتم‌های متاهیوریستیک آن است که در ابتدا یک یا چند راه‌حل اولیه را به عنوان نقطه شروع الگوریتم در نظر می‌گیرند و سپس با تکرار دنباله‌ای از مراحل، سعی در بهبود راه‌حل‌ها دارند. حال، به الگوریتم‌هایی که ابتدا فقط از یک راه‌حل اولیه مراحل الگوریتم بهینه‌سازی را آغاز می‌کنند، «مبتنی بر مسیر» ( trajectory-based) یا «متاهیوریستیک مبتنی بر یک جواب» (Single-Solution-based Metaheuristic) می‌گویند. بنابراین، در الگوریتم‌های مبتنی بر مسیر، یک جواب اولیه برای مسئله مورد نظر تعیین می‌‌شود و سپس همان یک راه‌حل به تدریج و با استفاده از یک سری قوانین، در حین فرایند حل مسئله بهبود می‌‌یابد تا به جواب بهینه برسد. در ادامه فهرستی از الگوریتم‌های مبتنی بر مسیر آورده‌ایم.
  • «شبیه سازی تبرید» (Simulated Annealing)
  • «الگوریتم جست و جوی ممنوعه» (Tabu Search)
  • «جستجوی تصادفی تطابقی حریصانه» (Greedy randomized adaptive search procedure | GRASP)
  • «جستجوی محلی تکراری» (Iterated Local Search)
  • «الگوریتم جستجوی محلی هدایت شده» (Guided Local Search)
  • «الگوریتم جستجوی متغیر محلی» (Variable Neighborhood Search)

• مبتنی بر جمعیت: الگوریتم‌های مبتنی بر جمعیت، از الگوریتم‌های متاهیوریستیکی به شمار می‌آیند که مجموعه‌ای از راه‌حل‌های اولیه را که به آن‌ها جمعیت گفته می‌شود، برای رسیدن به راه‌حل بهینه بهبود می‌دهند. در نهایت بهترین راه‌حل را میان آن جمعیت انتخاب می‌کنند. الگوریتم‌های مبتنی بر جمعیت نیز، به ۲ زیر بخش اصلی تقسیم می‌شوند که در ادامه به آن‌ها می‌پردازیم.

• • الگوربتم‌های تکاملی: الگوریتم‌های تکاملی از الگوریتم‌های مبتنی بر جمعیت به‌شمار می‌آیند که از فرایند تکامل زیستی در طبیعت مانند، تولید، جهش، ترکیب مجدد و انتخاب الهام گرفته است. الگوریتم‌های تکاملی معمولا راه‌حل‌های تقریبی مورد قبولی برای بسیاری از مسائل بهینه‌سازی ارائه می‌دهند. برخی از الگوریتم‌های تکاملی شامل موارد زیر هستند.
    • • «الگوریتم ژنتیک» ( Genetic Algorithm |GA)
      • «الگوریتم تکاملی تفاضلی» (Differential Evolution Algorithm)
      • «الگوریتم فرهنگی» (Cultural Algorithm)
  • الگوریتم‌های هوش ازدحامی: هوش ازدحامی نوعی یادگیری و تصمیم‌گیری جمعی بر اساس سیستم‌های غیر متمرکز و سازمان‌دهی شده است. الگوریتم‌های مبتنی بر هوش ازدحامی از فعالیت گروهی میان موجودات الهام گرفته‌اند. به عنوان مثال، گروهی از پرندگان یا ماهی‌ها را تصور کنید که بدون وجود رهبر و با همکاری یکدیگر به هدف مورد نظر خود که در اینجا یافتن راه‌حل بهینه است دست پیدا می‌کنند. به طور‌کلی هر ۲ نوع الگوریتم‌های تکاملی و مبتنی بر هوش ازدحامی، از دسته الگوریتم‌های متاهیوریستیک محسوب می‌شوند و برای حل مسائل پیچیده و با فضای جستجو بزرگ به کار می‌روند. در الگوریتم‌های هوش جمعی، گروهی از عوامل با هم همکاری می‌کنند تا هدفی مشترک برسند.اما، در الگوریتم‌های تکاملی، جمعیتی از افراد در طول زمان تکامل می‌کنند تا به پاسخ بهینه برسند. به‌طور کلی، الگوریتم‌ها مبتنی هوش ازدحامی دقیق‌تر و پایدارتر الگوریتم‌های بهینه‌سازی تکاملی عمل می‌کنند. با این حال، نتایج تجربی نشان داده است که الگوریتم‌های تکاملی نسبت به الگوریتم‌های مبتنی بر هوش ازدحامی سرعت اجرای بالا‌تری دارند. برخی از الگوریتم‌های مبتنی بر هوش ازدحامی شامل موارد زیر هستند.

تا اینجای مطلب، یاد گرفتیم، الگوریتم بهینه سازی چیست و با انواع آن‌ها آشنا شدیم. در ادامه، به چند نوع از الگوریتم‌های معروف و پرکاربرد بهینه‌سازی می‌پردازیم.

الگوریتم‌ های بهینه سازی معروف

در این قسمت از مطلب، چند الگوریتم بهینه‌سازی معروف را به اختصار توضیح می‌دهیم.

الگوریتم بهینه سازی شبیه سازی تبرید

الگوریتم «شبیه‌‌سازی تبرید» (Simulated Annealing) در سال ۱۹۸۳ توسط Kirkpatric ،Gelatt و Vecchi ابداع شد. این الگوریتم متاهیوریستیک می‌تواند برای مسائل بهینه‌سازی استفاده شود که در آن الگوریتم‌های دقیق شکست می‌خورند. این بهینه‌ساز برای تقریب پاسخ بهینه به‌ویژه در مسائل گسسته مانند مسئله فروشنده دوره‌گرد به کار می‌رود . نام این الگوریتم از فرایند «بازپخت» یا «انیلینگ»، در متالوژی گرفته شده‌ است که شامل ذوب و خنک کردن ماده‌ای، به منظور تغییر خواص فیزیکی آن است.

در الگوریتم شبیه سازی تبرید، هر نقطه در فضای جستجو معادل با حالتی از سیستم فیزیکی است، و مشابه با انرژی داخلی سیستم که باید کمینه شود، تابعی به نام (f(s – یا همان تابع هدف – تعیین می‌شود که باید کمینه شود. در این روش، هدف، انتقال سیستم از حالت اولیه دلخواه، به حالتی است که سیستم در آن کمترین انرژی را داشته باشد. در هر مرحله، این الگوریتم، حالت‌های همسایه احتمالی وضعیت فعلی s را ارزیابی می‌کند و به‌طور احتمالی بین انتقال سیستم به حالت بعدی یا ماندن در حالت کنونی تصمیم می‌گیرد. محاسبه این احتمالات در نهایت منجر به حرکت سیستم به سمت حالت‌های کم انرژی می‌شود. معمولا، این مرحله تا زمانی تکرار می‌شود که سیستم به حالتی برسد که به اندازه کافی خوب عمل می‌کند، یا به تعدادی از تکرار‌های مشخص برسد. در الگوریتم SA، بهینه‌ساز ابتدا یک راه‌حل اولیه را انتخاب می‌کند و سپس، از بین همسایگی، راه‌حلی جایگزین را انتخاب می‌کند. اگر Δf تغییر تابع هدف تعیین شده نسبت به قدم قبلی باشد و T دمای کنونی تعریف شده باشد، الگوریتم قدم بعدی را با توجه به شروط زیر طی می‌کند.

1. اگر 0> Δf باشد، آنگاه مقدار $$x$$ با $$x_{new}$$ جایگزین می‌شود.
2. اگر 0< Δf باشد، آنگاه با احتمال $$ p = exp(frac{Delta f}{-T}) $$ مقدار $$x$$ را با $$x_{n} $$ جایگزین می‌کنیم.

از تابع احتمال تعریف شده می‌توان به سادگی برداشت کرد که با ادامه فرایند بهینه‌سازی و کاهش دما، احتمال انتخاب راه‌حل‌های بدتر نیز به مرور زمان کاهش و با کاهش دما می‌یابد. در دماهای بالا، احتمال پذیرش راه‌حل بدتر زیاد است، بنابراین بهینه‌ساز فرصت بیشتری برای کاوش در فضای جستجو دارد. اما در دماهای پایین، احتمال پذیرش راه‌حل بدتر کم است، بنابراین بهینه‌ساز به تدریج به جواب بهینه نزدیک می‌شود.

در ادامه مراحل اجرای الگوریتم «SA» را آورده‌ایم.

1. یک راه‌حل اولیه را انتخاب می‌شود.
2. به طور تصادفی راه‌حلی جدید تولید می‌شود.
3. اگر راه‌حل جدید بهتر از راه‌حل اولیه باشد، آن را جایگزین راه‌حل اولیه کنید.
4. اگر راه‌حل جدید بدتر از راه‌حل اولیه باشد، احتمال جایگزینی راه‌حل جدید با توجه به میزان تغییر تابع هدف و دمای کنونی تعیین می‌شود.
5. دما را کاهش دهید.

مراحل ۲ تا ۵ را تکرار کنید تا به جواب بهینه برسید.

الگوریتم ژنتیک

الگوریتم ژنتیک نوعی الگوریتم بهینه‌سازی و جستجو است که از فرایند انتخاب طبیعی در تکامل زیستی الهام گرفته شده است. ایده پشت الگوریتم ژنتیک برای اولین بار توسط جان هالند در دهه ۱۹۶۰ معرفی شد. مفهوم الگوریتم ژنتیک بر اساس این ایده است که در طبیعت، موجودات زنده با محیط خود سازگار و به تدریج به گونه‌های برتر تبدیل می‌شوند. الگوریتم ژنتیک نیز از این روند برای یافتن راه‌حل‌های بهینه استفاده می‌کند. این الگوریتم‌ها را می‌توان در طیف گسترده‌ای از کاربردها از هوش مصنوعی و یادگیری ماشین گرفته تا تحقیقات اقتصادی و عملیاتی یافت که نشان‌دهنده تطبیق‌پذیری آن‌ها در حل مسائل مختلف است.

الگوریتم ژنتیک دائما از عملگرهای ژنتیکی برای تولید جمعیت‌های جدیدی از کروموزوم‌ها استفاده می‌کند. کروموزوم‌های موجود در هر جمعیت بر اساس عملکردشان ارزیابی می‌شوند. کروموزوم‌های با عملکرد بهتر، شانس بیشتری برای تولید فرزندان دارند. این فرایند تا زمانی ادامه می‌یابد که یک کروموزوم با عملکرد مطلوب پیدا شود یا تا زمانی که یک حد مشخصی از زمان یا تکرارها سپری شود.

در الگوریتم ژنتیک، راه‌حل‌ها به عنوان کروموزوم‌ها در نظر گرفته می‌شوند. هر کروموزوم در یک رشته از اعداد یا نمادها است که هر یک از این اعداد یک ژِن در نظر گرفته می‌شوند. مراحل این الگوریتم با ایجاد یک جمعیت اولیه از کروموزوم‌ها شروع می‌شود. سپس، از عملگرهای ژنتیکی برای تولید جمعیت جدیدی از کروموزوم‌ها استفاده می‌کند. عملگرهای ژنتیکی که در این بهینه‌ساز مورد استفاده قرار می‌گیرند شامل موارد زیر هستند.

• «ترکیب» ( Crossover): در تولید مثل، ۲ کروموزوم با هم ترکیب می‌شوند تا یک کروموزوم جدید تولید شود.
• «جهش» (Mutation): در جهش، یک تغییر تصادفی در یک کروموزوم ایجاد می‌شود.

فرایند اجرای الگوریتم ژنتیک شامل مراحل زیر است.

1. ایجاد جمعیت اولیه: جمعیتی اولیه از کروموزوم‌ها به طور تصادفی ایجاد می‌شود که تعداد کروموزوم‌ها در جمعیت اولیه معمولاً بزرگ است.
2. ارزیابی کروموزوم‌ها: در این مرحله، عملکرد هر کروموزوم در جمعیت ارزیابی می‌شود که عملکرد کروموزوم‌ها بر اساس تابع هدف مسئله بهینه‌سازی، تعیین می‌شود.
3. انتخاب کروموزوم‌ها: در این مرحله، کروموزوم‌های با عملکرد بهتر برای تولید فرزندان انتخاب می‌شوند که این امر با روش‌های مختلفی قابل انجام است.
4. ترکیب: کروموزوم‌های انتخاب‌شده با هم ترکیب می‌شوند تا فرزندان جدید تولید شوند.
5. جهش: تغییری تصادفی در یک یا چند کروموزوم ایجاد می‌شود. جهش به الگوریتم ژنتیک کمک می‌کند تا از تکرار شدن راه‌حل‌ها جلوگیری کند.
6. جایگزینی فرزندان: در این مرحله، فرزندان جدید جایگزین کروموزوم‌های موجود در جمعیت می‌شوند.

مراحل ۲ تا ۶ تا زمانی تکرار می‌شوند که یک کروموزوم با عملکرد مطلوب پیدا شود یا زمانی که حد مشخصی از زمان یا تکرارها سپری شود.

الگوریتم بهینه سازی ازدحام ذرات

پیش‌تر، یاد گرفتیم که مفهوم هوش ازدحامی در الگوریتم بهینه سازی چیست، اکنون در این بخش یکی از الگوریتم‌های مبتنی بر هوش ازدحامی، به نام «الگوریتم بهینه سازی ازدحام ذرات» (Particle Swarm Optimization | PSO) را به بیانی ساده توضیح می دهیم. الگوریتم بهینه سازی ازدحام ذرات از رفتار جمعی ذرات در طبیعت الهام گرفته است که در سال ۱۹۹۵ توسط جیمز کندی و راسل ابرهارت معرفی شد و اولین الگوریتم ارائه شده  مبتنی بر هوش ازدحامی است. الگوریتم PSO از جمعیتی از ذرات تشکیل شده است که هر ذره راه‌حلی برای مسئله بهینه‌سازی را نشان می‌دهد. این ذرات در فضای جستجو حرکت می‌کنند و با یکدیگر تعامل دارند و هر یک از موقعیتی تصادفی حرکت را آغاز می‌کنند تا به بهترین مکان برسند. حرکت ذرات توسط چند پارامتر اصلی تعیین می‌شود که در ادامه آورده‌ایم.

• «موقعیت» (Position): موقعیت هر ذره در فضای جستجو که بیانگر حالت فعلی ذره است.
• «سرعت» (Velocity): سرعت هر ذره در فضای جستجو نشانگر تغییرات موقعیت ذره در طول زمان است.
• «بهترین موقعیت هر ذره» (Personal Best): بهترین موقعیتی که هر ذره تاکنون در آن قرار گرفته‌ است.
• «بهترین موقعیت در بین تمامی ذرات» (Global Best): بهترین موقعیتی که در میان کل ذرات وجود داشته است.
• «پارامتر وزن» (Weight): مقدار پارامتر وزن بین ۰ و ۱ قرار دارد. این مقدار تعیین می‌کند که چقدر از سرعت قبلی ذره بر سرعت جدید می‌تواند تاثیرگذار باشد. اگر وزن به ۱ نزدیک باشد، سرعت جدید به‌طور کامل تحت تأثیر سرعت قبلی قرار می‌گیرد. اما اگر وزن به صفر نزدیک باشد، سرعت جدید به مراتب کمتر، تحت تأثیر سرعت قبلی قرار می‌گیرد.

به زبان ساده، الگوریتم PSO به صورت زیر عمل می‌کند.

1.  جمعیت اولیه‌ای از ذرات تولید می‌شود.
2. سرعت هر ذره به طور تصادفی تعیین می‌شود.
3. بهترین موقعیت هر ذره تا‌کنون ثبت می‌شود.
4. بهترین موقعیت در میان تمامی ذرات مشخص می‌شود.
5. ذرات بر اساس ویژگی‌های تعیین شده در مراحل قبل، حرکت می‌کنند.

مراحل ۲ تا ۵ برای رسیدن به پاسخ بهینه تکرار می‌شود.

خلاصه‌ ای از مطلب

در این مطلب از مجله فرادرس، ابتدا یاد گرفتیم که الگوریتم بهینه سازی چیست. سپس، به این نکته پرداختیم که برای انتخاب الگوریتم بهینه‌سازی مناسب برای یک مسئله، بهتر است با تعریف مسئله بهینه‌سازی، ویژگی‌ها و انواع آن‌ها آشنا باشیم. به همین منظور، به چند نوع طبقه‌بندی مرسوم در مسائل بهینه‌سازی پرداختیم. در ادامه، به ۲ دسته اصلی از الگوریتم‌های بهینه‌سازی پرداختیم که شامل بهینه‌سازی قطعی و بهینه‌سازی تقریبی هستند. در بهینه‌سازی قطعی، الگوریتم‌ها به صورت تئوری تضمین می‌کنند که بهترین راه‌حل را برای مسائل پیدا کنند، اما این الگوریتم‌ها ممکن است در فضاهای جست‌وجوی بزرگ و پیچیده کارایی نداشته باشند.

الگوریتم‌های قطعی شامل ۲ زیر مجموعه روش تکرار شونده و شمارشی هستند. در روش‌های تکرار شونده الگوریتم از یک نقطه تصادفی شروع و با تکرار مراحل به سمت موقعیت بهینه حرکت می‌کند. مثالی از این دسته از الگوریتم‌ها، روش «گرادیان کاهشی» (Gradient Descent) است که الگوریتم در هر مرحله به سمت خلاف جهت گرادیان – نسبت به متغیرهای مستقل – حرکت می‌کند تا به مقدار کمینه‌ای از تابع هدف برسد. روش‌های شمارشی نیز تمام ترکیب‌های ممکن از راه‌حل‌های امکان‌پذیر را در نظر می‌گیرند تا نقطه بهینه را پیدا کنند که این روش‌ها در مسائل گسسته و محدود کارایی بیشتری دارند.

در ادامه مطلب، الگوریتم‌های بهینه‌سازی تقریبی را معرفی کردیم که سعی دارند راه‌حل‌های تقریبا بهینه برای مسائل پیچیده‌تر ارائه دهند. این الگوریتم‌ها معمولاً در مواقعی که یافتن راه‌حل دقیق، غیرممکن یا زمان‌بر است، مورد استفاده قرار می‌گیرند. الگوریتم‌های بهینه‌سازی تقریبی نیز به ۲ زیرشاخه الگوریتم‌های هیوریستیک و متاهیوریستیک تقسیم می‌شوند. به طور کلی، الگوریتم‌های بهینه‌سازی هیوریستیک و متاهیوریستیک به دنبال یافتن پاسخی نزدیک بهینه هستند.

در ادامه، یاد گرفتیم که تفاوت مفاهیم هیوریستیک و متاهیوریستیک در الگوریتم بهینه سازی چیست، تفاوت اصلی بین الگوریتم‌های هیوریستیک و متاهیوریستیک در این است که الگوریتم‌های هیوریستیک برای حل یک مسئله خاص طراحی می‌شوند، در حالی که الگوریتم‌های متاهیوریستیک برای حل انواع مسائل، طراحی می‌شوند. الگوریتم‌های هیوریستیک را می‌توان به ۲ دسته کلی هیوریستیک سازنده و جست‌وجوی محلی تقسیم‌بندی کرد. در هیوریستیک سازنده، مسئله به چندین زیرمسئله تقسیم شده و هر یک از این زیرمسائل به صورت جداگانه حل شده و نتایج جزئی با هم ترکیب می‌شوند تا به یک نتیجه کلی برسد. این روش زمانی مورد استفاده قرار می‌گیرد که حل کل یک مسئله به صورت مستقیم با مشکل مواجه می‌شود.

در جست‌وجوی محلی، الگوریتم یک نقطه به صورت تصادفی به عنوان راه‌حل اولیه انتخاب می‌شود و در هر مرحله با اعمال تغییرات جزئی به راه‌حل مرحله قبل سعی در بهبود راه‌حل ارائه شده دارد. این الگوریتم‌ها پس از انتخاب یک نقطه تصادفی به عنوان راه‌حل اولیه، تغییرات کوچک و جزئی در راه‌حل اعمال می‌کنند تا بهبودی در پاسخ مسئله حاصل شود. در ادامه به الگوریتم‌های مبتنی بر ازدحام ذرات و الگوریتم‌های تکاملی نیز پرداختیم که زیر مجموعه‌ای از روش‌های متاهیوریستیک به شمار می‌آیند. سپس، برخی از الگوریتم‌های معروف بهینه‌سازی را به اختصار توضیح دادیم. در ادامه، به پرسش‌های متداول در مورد الگوریتم‌های بهینه‌سازی پاسخ می‌دهیم.

سوالات متداول

تا این بخش از مطلب یاد گرفتیم که الگوریتم بهینه سازی چیست و با انواع  آن‌ها آشنا شدیم. همچنین، در ادامه چند الگوریتم معروف بهینه‌سازی را به اختصار مورد بررسی قرار دادیم. در ادامه، برخی از سوالات متداول پیرامون الگوریتم‌های بهینه‌سازی را بیان می‌کنیم.

تفاوت بین الگوریتم‌های مبتنی بر هوش ازدحامی و تکاملی چیست؟

هر ۲ از الگوریتم‌های بهینه‌سازی متاهیوریستیک به‌ شمار می‌آیند با این تفاوت که الگوریتم‌های تکاملی بر مبنای مفهوم تکامل و وراثت موجود در طبیعیت عمل می‌کند. این در حالی است که، الگوریتم‌های مبتنی بر هوش ازدحامی رفتار‌های جمعی ذرات موجود در طبیعت را مدل‌سازی می‌کنند. برای مثال، روش‌های مبتنی بر هوش ازدحامی از عملکرد جمعی گرو‌ه‌های حیوانات مانند حشرات، پرندگان و ماهی‌ها الگو‌برداری می‌کنند.

تفاوت بین الگوریتم های تقریبی و قطعی چیست؟

الگوریتم‌های قطعی مزیت دقت را دارند، اما نیاز به توان محاسباتی زیادی دارند. الگوریتم‌های تقریبی مزیت سرعت را دارند اما دقت کمتری را ارائه می‌دهند.

تفاوت بین روش های هیوریستیک و روش های متاهیوریستیک چیست؟

الگوریتم‌های بهینه‌سازی هیوریستیک و متاهیوریستیک هر دو به دنبال یافتن پاسخی نزدیک به بهینه برای مسائل بهینه‌سازی هستند. اما، تفاوت اصلی بین این دو دسته از الگوریتم‌ها در این است که الگوریتم‌های هیوریستیک به طور خاص برای حل یک مسئله خاص طراحی می‌شوند، در حالی که الگوریتم‌های متاهیوریستیک به شکل عمومی‌تر و مستقل از جزئیات خاص مسئله طراحی می‌شوند.

جمع بندی

در این مطلب از مجله فرادرس، ابتدا به این موضوع پرداختیم که الگوریتم بهینه سازی چیست. سپس، به ضرورت آشنایی با مسائل بهینه‌سازی، ویژگی‌ها و انواع آن‌ها پرداختیم. آشنایی با انواع مسائل بهینه‌سازی، انتخاب الگوریتم بهینه‌سازی مناسب را تسهیل می‌کند. در ادامه، الگوریتم‌های بهینه‌سازی قطعی و تقریبی مورد بررسی قرار گرفتند. الگوریتم‌های بهینه‌سازی قطعی از دو زیرمجموعه روش تکرار شونده و شمارشی تشکیل شده‌اند که هرکدام به ترتیب از روش‌های تکراری و ترکیبی بهره می‌برند.

الگوریتم‌های بهینه‌ساز تقریبی نیز به روش‌های هیوریستیک و متاهیوریستیک تقسیم می‌شوند. این الگوریتم‌ها راه‌حلی را ارائه می‌دهند که لزوما راه‌حل بهینه نیست، اما نزدیک به جواب بهینه هست. الگوریتم‌های متاهیوریستیک مستقل از جزئیات مسئله و برای حل انواع زیادی از مسائل طراحی می‌شوند.در ادامه الگوریتم شبیه‌سازی تبرید به عنوان الگوریتم مبتنی بر مسیر و الگوریتم ژنتیک به عنوان یکی از الگوریتم‌های مهم تکاملی مورد بررسی قرار گرفتند و در نهایت نیز، اشاره‌ای به یکی از اولین الگوریتم‌های ارائه شده در حوزه هوش ازدحامی داشتیم.