۱۵ بازدید

آخرین به‌روزرسانی: ۲۹ بهمن ۱۴۰۲

زمان مطالعه: ۴ دقیقه

شیب یک خط از مبانی هندسه در ریاضیات به شمار می‌آید و کاربردهای زیادی در مهندسی دارد. از جمله کاربردهای آن می‌توان در ساختمان سازی، پل‌سازی، راه‌سازی و غیره اشاره کرد. شیب هر خط را می‌توان با داشتن دو نقطه روی صفحه محاسبه کرد. فرمول شیب خط در واقع نسبت تغییرات عمودی به تغییرات افقی بین دو نقطه منحصر بفرد روی یک خط راست است. در این مطلب از مجله فرادرس با مفهوم شیب خط در ریاضی آشنا خواهیم شد. برای درک بهتر این موضوع چند مثال و تمرین بیان می‌شود. پس اگر به این موضوع علاقه‌مند هستید ادامه این مطلب را مطالعه کنید.

شیب چیست؟

طبق تعریف، مقدار تغییرات در مختصات Y نسبت به مقدار تغییرات در مختصات X مربوط به یک خط راست، شیب خط می‌گویند. مقدار تغییرات در مختصات Y را به صورت $$triangle y$$ و مقدار تغییرات در مختصات X را به صورت $$triangle x$$ نمایش می‌دهند. به شکل زیر توجه کنید.

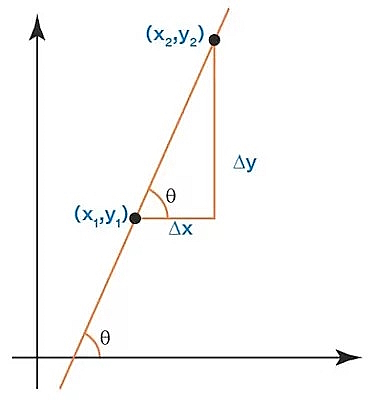
مطابق شکل فوق دو نقطه از خط یعنی نقطه اول x₁ و y₁ و نقطه دوم  x_{2 و} y₂ را انتخاب می‌کنیم و تغییرات را مطابق رابطه زیر بدست می‌آوریم:

$$m=frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=frac{triangle y}{triangle x}$$

که در رابطه فوق m شیب خط هست.

توجه کنید که راه دیگری برای محاسبه شیب خط وجود دارد و آن استفاده از تانژانت زاویه آن خط است:

$$tan theta=frac{triangle y}{triangle x}$$

که در رابطه فوق مقدار تانژانت زاویه برابر شیب خط مورد نظر خواهد بود.

فرمول شیب خط

شیب یک خط را می‌توانیم از معادله یک خط راست نیز بدست آوریم. معادله خط راست به صورت زیر است.

$$y=mx+b$$

عوامل به کار رفته در رابطه فوق به شرح زیر است:

• m: شیب خط که مقدار آن نیز برابر $$frac{triangle y}{triangle x}$$ است.
• b: عرض از مبدا نام دارد که نقطه هست که خط محور عمودی را قطع می‌کند.
• x: محور افقی مختصات نامیده می‌شود.
• y: محور عمودی مختصات نام دارد.

به مثال‌های زیر توجه کنید تا استفاده از فرمول شیب خط را بهتر یاد بگیرید.

مثال اول شیب یک خط

شیب یک خط که شامل نقاط $$(5,5)$$ و $$(4,2)$$ است را حساب می‌کنیم.

پاسخ:

مطابق روابط گفته شده اختلاف نقاط روی محور عمودی را بر اختلاف نقاط روی محور افقی تقسیم می‌کنیم.

$$m=frac{y_{2}-y_{1}}{x_{2}-x_{1}}=frac{5-2}{5-4}=3$$

بنابراین شیب بدست آمده برابر ۳ خواهد بود.

مثال دوم شیب یک خط

می‌خواهیم شیب یک خط که شامل نقاط $$(-1,8.5)$$ و $$(3,-6.25)$$ است را حساب کنیم.

مانند مثال قبل اختلاف نقاط روی محور عمودی را بر اختلاف نقاط روی محور افقی تقسیم می‌کنیم.

$$m=frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$

$$m=frac{8.5-(-6.25)}{-1-3}=frac{14.75}{-4}=-3.6875$$

بنابراین شیب بدست آمده برابر ۳٫۶۸۷۵- خواهد بود.

مثال سوم شیب یک خط

می‌خواهیم با توجه به نمودار زیر شیب خط را حساب کنیم.

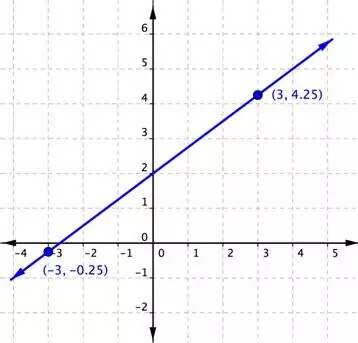
ابتدا باید دو نقطه که روی خط هستند را انتخاب کنیم که در اینجا نقطه اول $$(3,4.25)$$ و نقطه دوم $$(-3,-0.25)$$ است.

$$m=frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$

$$m=frac{4.25-(-0.25)}{3-(-3)}=frac{4.5}{6}=0.75$$

انواع شیب

می‌توانیم شیب را براساس مقدار و علامتی که می‌گیرد به صورت زیر دسته‌بندی کنیم:

• شیب مثبت
• شیب منفی
• شیب صفر
• شیب تعریف نشده
• شیب خطوط عمود برهم
• شیب خطوط موازی

شیب مثبت

در نمودارها همیشه از چپ به راست خط را بررسی می‌کنیم اگر شیب خط به طوری باشد که مختصاتش در محور عمودی افزایش پیدا کند به اصطلاح می‌گوییم شیب خط مثبت است. توجه کنید که در این حالت $$triangle y>0$$ و علامت m نیز مثبت می‌شود.

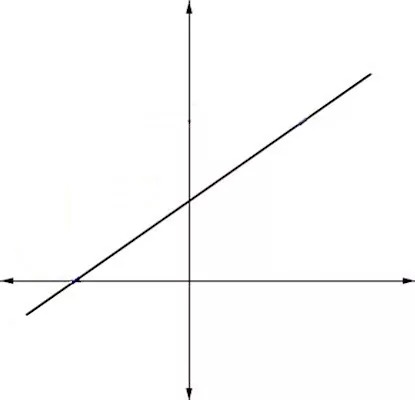
شیب منفی

اگر شیب خط به طوری باشد که مختصاتش در محور عمودی کاهش پیدا کند به اصطلاح می‌گوییم شیب خط منفی است. توجه کنید که در این حالت $$triangle y<0$$ و علامت m نیز منفی می‌شود.

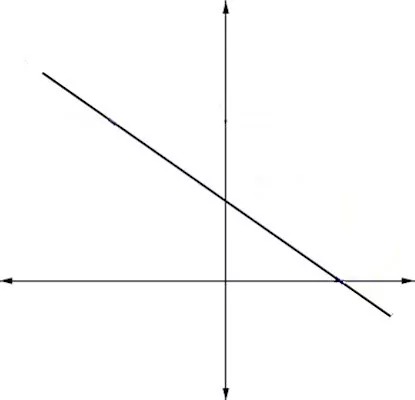
شیب صفر

هر گاه مختصات عمودی یک خط بدون تغییر باشد، آنگاه می‌گوییم شیب خط صفر است. در این حالت $$m=0$$ و $$triangle y=0$$ می‌شود.

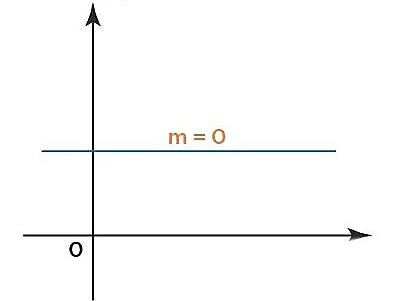
شیب تعریف نشده

هر گاه مختصات افقی یک خط بدون تغییر باشد، آنگاه می‌گوییم شیب خط تعریف نشده است به عبارت دیگر در رابطه‌ای که برای شیب گفته شد، مخرج کسر صفر می‌شود. در این حالت $$triangle x=0$$ هست.

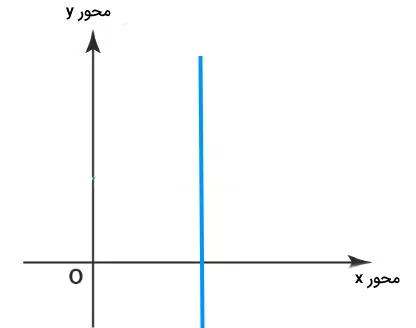
شیب خطوط موازی

هرگاه حداقل دو خط راست به طوری در دستگاه مختصات قرار گیرند که هیچگاه یکدیگر را قطع نکنند، آنگاه آن دو را موازی می‌گوییم. در این حالت شیب دو خط همیشه با هم برابر است.

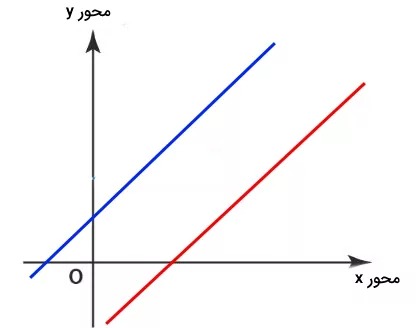
مثال اول خطوط موازی

می‌خواهیم شیب خطی را پیدا کنیم که موازی با خط به معادله $$y=−3x+4$$ باشد.

پاسخ:

با توجه به معادله فوق شیب خط برابر ۳- است و هر خط موازی با آن نیز باید همین مقدار شیب را داشته باشد.

مثال دوم خطوط موازی

می‌خواهیم بررسی کنیم که آیا دو خط با معادله $$y=6x+5$$ و $$y=6x-1$$ با هم موازی هستند یا نه.

پاسخ:

در معادله خط راست، ضریب x شیب خط هست و چون در هر دو معادله فوق ضریب x برابر ۶ است بنابراین این دو خط با هم موازی هستند.

شیب خطوط عمود برهم

هرگاه حداقل دو خط راست که با یکدیگر زاویه ۹۰ درجه تشکیل دهند، آن دو خط را عمود برهم می‌نامیم. در این صورت حاصل ضرب شیب آن دو در یکدیگر برابر ۱- خواهد شد.

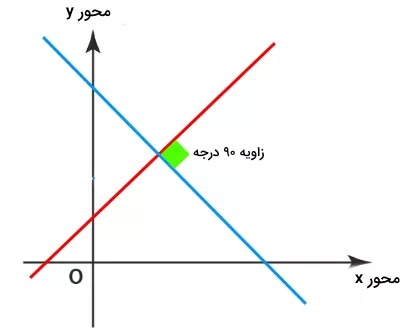
مثال اول خطوط عمود برهم

خطی به معادله $$y=2x-6$$ داریم که می‌خواهیم یک خط دیگر عمود بر آن را پیدا کنیم.

پاسخ:

از آنجا که در معادله خط راست، ضریب x شیب خط هست، پس شیب در معادله فوق برابر ۲ است. اگر بخواهیم یک خط دیگر عمود بر آن پیدا کنیم شیب آن باید معکوس و قرینه این معادله باشد یعنی $$m=-frac{1}{2}$$.

مثال دوم خطوط عمود برهم

می‌خواهیم وضعیت دو خط $$y=−8x+5$$ و $$displaystyle y,text{=},,frac{1}{8}x-1$$ را نسبت به هم بررسی کنیم.

پاسخ:

ابتدا باید ضریب x را برای شیب دو خط بررسی کنیم. شیب در معادله اول برابر $$-8$$ هست در حالی که شیب در معادله دوم برابر $$frac{1}{8}$$ است. چون این دو مقدار باهم برابر نیستند پس دو خط موازی نیستند. همچنین اگر این دو مقدار را در هم ضرب کنیم صفر می‌شود پس این دو خط برهم عمود هستند.

تمرین‌های شیب خط

اکنون که با مفهوم شیب خط و نحوه محاسبه آن آشنا شدید چند تمرین در این قسمت برای بالا بردن سطح مهارت در این موضوع قرار داده شده است.

در شکل زیر شیب خط را محاسبه کنید.

مشاهده جواب

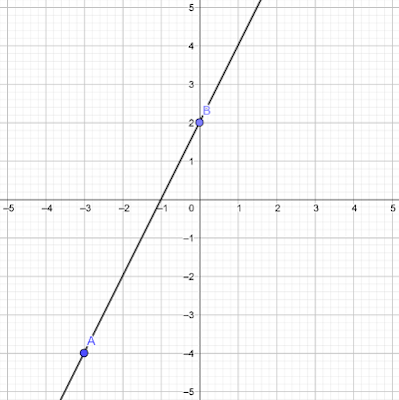
برای محاسبه شیب خط راست به دو نقطه نیاز داریم. نقاطی که در شکل مشخص شده‌اند $$(-3,-4)$$ و $$(0,2)$$ را انتخاب می‌کنیم و در معادله زیر قرار می‌دهیم:

$$m=frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$

سپس نقاط را داخل رابطه جایگذاری می‌کنیم:

$$m=frac{{2}-(-4)}{0-(-3)}=frac{6}{3}=2$$

با استفاده از شکل زیر شیب خط را حساب کنید.

مشاهده جواب

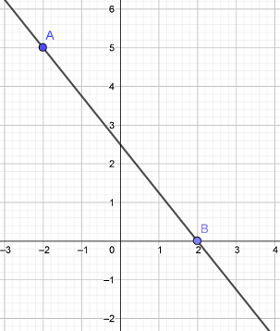
برای محاسبه شیب خط باید دو نقطه از خط را داشته باشیم. با توجه به شکل نقطه A با مختصات $$(-2,5)$$ و نقطه B با مختصات $$(2,0)$$ را داریم و در رابطه زیر جایگذاری می‌کنیم.

$$m=frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$

$$m=frac{{0}-(5)}{2-(-2)}=frac{-5}{4}$$

با توجه به شکل زیر شیب خط افقی را بدست آورید.

مشاهده جواب

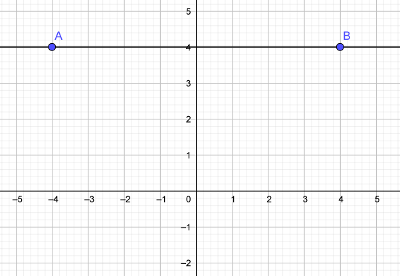
برای محاسبه شیب خط راست به دو نقطه نیاز داریم. نقاط A و B که در شکل مشخص شده‌اند به ترتیب $$(-4,4)$$ و $$(4,4)$$ هستند که در معادله زیر قرار می‌دهیم:

$$m=frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$

$$m=frac{{4}-(4)}{4-(-4)}=frac{0}{8}=0$$

هما‌طور که در متن اشاره شد شیب خط افقی صفر است.

شیب خطی که از نقاط $$(-1,-1)$$ و $$(1,3)$$ عبور می‌کند را حساب کنید.

مشاهده جواب

نقاط داده شده را در رابطه قرار می‌دهیم و شیب خط را حساب می‌کنیم.

$$m=frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$

$$m=frac{{-1}-(-3)}{-1-(-1)}=frac{-4}{-2}=2$$

شیب خطی که از نقاط $$(2,0)$$ و $$(2,3)$$ عبور می‌کند را حساب کنید.

مشاهده جواب

نقاط داده شده را درون رابطه جایگذاری می‌کنیم تا شیب خط را حساب کنیم.

$$m=frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$

$$m=frac{{3}-(0)}{2-(2)}=frac{3}{0}$$

همان‌طور که مشاهده می‌کنید مخرج کسر صفر شده و شیب تعریف نشده است بنابراین این یک خط عمودی است.

شیب خط در معادله $$y-1=5x+2$$ را بیابید.

مشاهده جواب

ابتدا باید معادله را به شکل استاندارد تبدیل کنیم.

$$y=5x+2+1rightarrow y=5x+3$$

اکنون که معادله استاندارد شد، ضریب x همان شیب خط است یعنی ۵

شیب خط در معادله $$2y-3x=5$$ را پیدا کنید.

مشاهده جواب

ابتدا باید معادله را به شکل استاندارد مظابق آن‌چه در متن آمده تبدیل کنیم.

$$2y-3x=5rightarrow y=frac{3}{2}x+frac{5}{2}$$

اکنون که معادله به شکل استاندارد تبدیل شده است، ضریب x شیب خط می‌شود یعنی $$frac{3}{2}$$.

وضعیت دو خط به معادله $$y=3x-2$$ و $$x+3y+5=0$$ را نسبت به هم بیابید.

مشاهده جواب

معادله اول شکل استاندارد دارد ولی معادله دوم را باید به شکل استاندارد تبدیل کنیم.

$$x+3y+5=0rightarrow 3y=-x-5rightarrow y=-frac{1}{3}x-frac{5}{3}$$

اکنون شیب هر دو معادله را داریم، شیب در معادله اول برابر ۳ و شیب در معادله دوم برابر $$-frac{1}{3}$$ است. چون این دو مقدار مساوی نیستند پس این دو خط موازی نخواهند بود. 

با ضرب شیب دو معادله در یکدیگر خواهیم داشت:

$$-frac{1}{3}times3=-1$$

بنابراین دو خط عمود برهم هستند.

 

نتیجه‌گیری

در این مطلب از مجله فرادرس با مفهوم شیب خط و انواع آن آشنا شدید همچنین نحوه محاسبه شیب خط با استفاده از فرمول $$y=mx+b$$ را آموختید. مثال‌ها و تمرین‌هایی نیز برای افزایش درک این موضوع ارائه شد. دانستن شیب خط و محاسبه آن می‌تواند در مباحث بسیاری در هندسه و مهندسی کارآمد باشد.