دسته‌بندی‌های مختلفی برای تعریف انواع الگوریتم‌های یادگیری ماشین وجود دارد و رایج‌ترین روش، تقسیم الگوریتم‌ها بر اساس هدف مسئله است. به‌طور کلی، روش‌های یادگیری ماشین در سه گروه «نظارت شده» (Supervised)، «نظارت نشده» (Unsupervised) و «تقویتی» (Reinforcement) قرار می‌گیرند. در این بین، الگوریتم های یادگیری نظارت شده بیشترین کاربرد را داشته و با استفاده از مجموعه‌داده‌های برچسب‌گذاری شده، برای پیش‌بینی دقیق خروجی آموزش داده می‌شوند. در این مطلب از مجله فرادرس، انواع الگوریتم های یادگیری نظارت شده و کاربردهای آن‌ها را مرور می‌کنیم. الگوریتم های یادگیری نظارت شده در حل مسائل متنوعی از جمله دسته‌بندی ایمیل‌های عادی از اسپم به کمک سازمان‌های بزرگ می‌آیند. در این مطلب، ابتدا شرح مختصری از یادگیری نظارت شده ارائه داده و سپس به معرفی و بررسی نحوه کارکرد چند نمونه رایج و متداول از الگوریتم های یادگیری نظارت شده می‌پردازیم.

انواع الگوریتم های یادگیری نظارت شده

الگوریتم های یادگیری نظارت شده با بهره‌گیری از «متغیرهای مستقل» (Independent Variables) یا همان «ویژگی‌ها» (Features)، متغیر هدف یا همان «وابسته» (Dependent Variable) را پیش‌بینی می‌کنند. در این مطلب، به معرفی الگوریتم های یادگیری نظارت شده زیر می‌پردازیم:

• «رگرسیون خطی» (Linear Regression)
• «ماشین بردار پشتیبان» (Support Vector Machine | SVM)
• «بیز ساده» (Naive Bayes)
• «رگرسیون لجستیک» (Logistic Regression)
• «K-نزدیک‌ترین همسایه» (K-Nearest Neighbors | KNN)
• «درخت تصمیم» (Decision Tree)
• «جنگل تصادفی» (Random Forest)
• «درخت تصمیم تقویت شده با گرادیان» (Gradient Boosted Decision Tree | GBDT)

نوع الگوریتم یادگیری نظارت شده به خصوصیات متغیر هدف بستگی داشته و می‌تواند در دو گروه «دسته‌بندی» (Classification) برای داده‌های گسسته یا «رگرسیون» (Regression) برای مقادیر پیوسته قرار بگیرد. در ادامه این مطلب از مجله فرادرس به بررسی دقیق‌تر هر یک از روش‌های عنوان شده در فهرست بالا می‌پردازیم.

الگوریتم رگرسیون خطی

هدف «رگرسیون خطی» (Linear Regression)، برازش معادله‌ای خطی بر داده‌ها از طریق مدل‌سازی رابطه میان متغیر هدف و یک یا چند متغیر مستقل است. همان‌طور که از اسمش پیداست، متغیر هدف مانند قیمت، مساحت یا طول یک شیء، حاوی مقداری پیوسته است. رگرسیون خطی زمانی بهترین عملکرد را دارد که رابطه‌ای خطی میان متغیرهای مستقل با متغیر هدف برقرار باشد. ابزارهای مختلفی برای کشف ارتباط میان متغیرها وجود دارند که از جمله این ابزارها می‌توان به «نمودار نقطه‌ای» (Scatter Plot) و «ماتریس همبستگی» (Correlation Matrix) اشاره کرد. به عنوان مثال، نمودار نقطه‌ای زیر، نشان‌گر نوعی همبستگی مثبت میان دو متغیر است؛ به این شکل که با افزایش یک متغیر، مقدار متغیر دیگر نیز افزایش پیدا می‌کند.

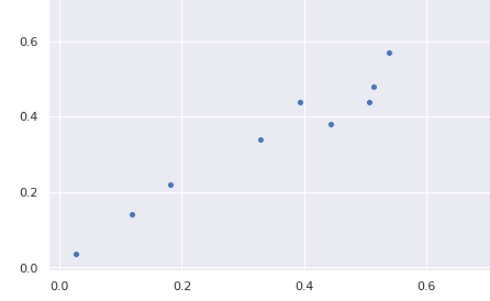
تلاش رگرسیون خطی به عنوان یکی از انواع الگوریتم های یادگیری نظارت شده، برازش خطی رگرسیونی بر نقاط داده‌ایست که رابطه یا همبستگی میان نقاط داده را به خوبی نمایش می‌دهند. با استفاده از رایج‌ترین تکنیک رگرسیون خطی یعنی روش «حداقل مربعات عادی» (Ordinary Least Squares | OLE)، بهترین معادله خط از طریق کمینه‌سازی مجموع مربعات فاصله میان نقاط داده و خط رگرسیونی حاصل می‌شود. خط رگرسیونی که با استفاده از روش حداقل مربعات عادی یا به اختصار OLE، برای نقاط داده تصویر قبلی به‌دست می‌آید، مانند نمودار زیر است:

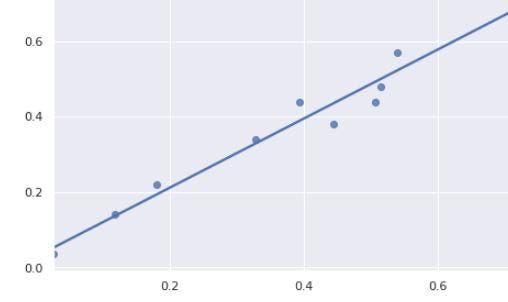
در این مثال، یک متغیر مستقل و یک متغیر هدف داریم. قابل ذکر است که رگرسیون خطی، در مسائلی که از چند متغیر مستقل تشکیل شده‌اند نیز کاربرد دارد.

الگوریتم ماشین بردار پشتیبان

بیشترین استفاده «ماشین بردار پشتیبان»‌ (Support Vector Machine | SVM) در مسائل دسته‌بندی است. اما در مسائل رگرسیون نیز کاربرد دارد. در این روش، کلاس‌های مختلف از طریق خطی به‌نام «مرز تصمیم» (Decision Boundary) از یک‌دیگر جدا می‌شوند. طریقه رسم و شناسایی مرز تصمیم، مهم‌ترین بخش الگوریتم ماشین بردار پشتیبان است. پیش از ترسیم مرز تصمیم، تمامی نقاط داده یا «مشاهدات» (Observations) بر صفحه‌ای n بعدی نگاشت می‌شوند. به عنوان مثال اگر از دو ویژگی طول و عرض برای دسته‌بندی سلول‌های مختلف استفاده کنیم، فضای نقاط داده دو بعدی و مرز تصمیم نیز یک خط خواهد بود. اگر تعداد ویژگی‌ها بیش از سه باشد، مرز تصمیم به «ابَر صفحه‌ای» (Hyperplane) تبدیل می‌شود که رسم آن دشوار است.

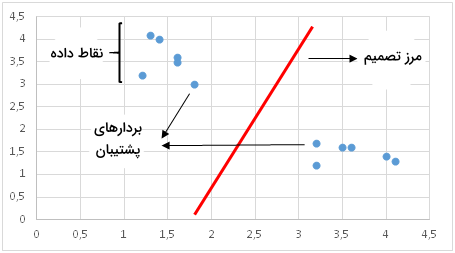
نحوه ترسیم مرز تصمیم به گونه‌ایست که فاصله میان بردارهای پشتیبان حداکثر شود. اگر مرز تصمیم بیش از حد به یک بردار پشتیبان نزدیک باشد، یعنی مدل حساس به نویز بوده و قابلیت تعمیم مناسبی ندارد. در چنین موقعیتی، ممکن است حتی تغییرات جزئی در متغیرهای مستقل نیز باعث «دسته‌بندی اشتباه» (Misclassification) شوند.

الگوریتم بیز ساده

روش «بیز ساده» (Naive Bayes) از جمله الگوریتم های یادگیری نظارت شده است که در مسائل دسته‌بندی مورد استفاده قرار می‌گیرد. از همین جهت به آن «دسته‌بند بیز ساده» (Naive Bayes Classifier) نیز گفته می‌شود. در این روش، فرض می‌شود ویژگی‌ها از یک‌دیگر مستقل بوده و هبستگی میان آن‌ها وجود ندارد. با این حال در زندگی حقیقی شرایط متفاوت است. به‌خاطر همین دیدگاه ساده انگارانه است که آن را بیز «ساده» می‌نامند. «قضیه بیز» (Bayes Theorem)، الهام‌بخش ایده اصلی الگوریتم بیز ساده است:

$$ p(A|B) = frac{p(A)cdotp(B|A)}{p(B)} $$

توضیح هر یک از نمادهای به‌کار رفته در قضیه بیز به شرح زیر است:

• $$ p(A|B) $$: احتمال پیشامد $$ A $$ با فرض وقوع پیشامد $$ B $$.
• $$ p(B|A) $$: احتمال پیشامد $$ B $$ با فرض وقوع پیشامد $$ A $$.
• $$ p(A) $$: احتمال پیشامد $$ A $$.
• $$ p(B) $$: احتمال پیشامد $$ B $$.

دسته‌بند بیز ساده، احتمال یک کلاس مشخص را به شرط وجود مجموعه‌ای از «مقادیر ویژگی» (Feature Values) محاسبه می‌کند. با جایگذاری این قاعده در قضیه بیز به چنین عبارتی می‌رسیم:

$$ p(y_i|x_1, x_2, …,x_n) = frac{p(x_1, x_2,…,x_n|y_i)cdotp(y_i)}{p(x_1, x_2,…,x_n)} $$

عبارت احتمالاتی $$ p(x_1, x_2,…,x_n|y_i) $$، بیان‌گر ترکیب مشخصی از ویژگی به شرط وجود یک برچسب کلاسی است. محاسبه این عبارت به مجموعه‌داده‌هایی جامع، برای تخمین احتمال توزیع ترکیب‌های مختلف از مقادیر ویژگی نیاز دارد. فرض مستقل بودن ویژگی‌ها از یک‌دیگر، راه‌حل الگوریتم بیز ساده برای غلبه‌بر این مشکل است. در ادامه و از آن‌جایی که مخرج معادله، تنها احتمال کلاسی مشخص را نسبت به یک نمونه نرمال‌سازی می‌کند، عبارت $$ p(x_1, x_2,…,x_n) $$ نیز به‌منظور ساده‌سازی بیشتر حذف می‌شود. محاسبه احتمال کلاس $$ y_i $$ از طریق معادله زیر صورت می‌گیرد:

با فرض مستقل بودن ویژگی‌ها، عبارت $$ p(x_1, x_2,…,x_n|y_i) $$ مانند نمونه بسط داده می‌شود:

$$ p(x_1, x_2,…,x_n | y_i) = p(x_1|y_i)cdotp(x_2|y_i)cdot…cdotp(x_n|y_i) $$

با فرض وجود کلاس $$ y_i $$، تخمین احتمال شرطی یک ویژگی از طریق داده‌ها به مراتب راحت‌تر است. در این حالت، الگوریتم باید توزیع احتمال تمامی ویژگی‌ها را برای هر کلاس به‌صورت مستقل ذخیره کند. برای مثال اگر تعداد ۵ کلاس و ۱۰ ویژگی داشته باشیم، باید ۵۰ مورد توزیع احتمال مختلف ذخیره شوند. در نتیجه، محاسبه احتمال مشاهده یک کلاس به شرط وقوع چند ویژگی، به عملی ساده برای الگوریتم بیز تبدیل می‌شود.

الگوریتم رگرسیون لجستیک

تکنیک «رگرسیون لجستیک» (Logistic Regression) یکی از رایج‌ترین الگوریتم های یادگیری نظارت شده است که اغلب در مسائل «دسته‌بندی دودویی» (Binary Classification) کاربرد دارد. اگرچه عبارت «رگرسیون» با «دسته‌بندی» در تضاد است، در این‌جا منظور از عبارت «لجستیک»، «تابع لجستیکی» (Logistic Function) است که عمل دسته‌بندی را در این الگوریتم انجام می‌دهد. رگرسیون لجستیک در عین سادگی، بسیار در مسائل دسته‌بندی موثر است. این الگوریتم راه‌حل‌های کارآمدی برای موضوعاتی همچون نرخ «ریزش مشتری» (Customer churn)، دسته‌بندی ایمیل‌های اسپم و پیش‌بینی تعداد تبلیغات مشاهد شده توسط کاربران ارائه می‌دهد. تابع لجستیک، پایه و اساس رگرسیون لجستیک است که به آن تابع «سیگموئید» (Sigmoid) نیز گفته می‌شود. ورودی تابع سیگموئید اعداد حقیقی و خروجی آن در بازه ۰ تا ۱ قرار دارد.

$$ Sigmoid = y = frac{1}{1 + e^{-x}} $$

فرض کنید می‌خواهیم معادله خطی زیر را حل کنیم:

$$ z = beta_0 + beta_1cdot x_1 + … +beta_ncdot x_n $$

مدل رگرسیون لجستیک، معادله‌ای خطی را به عنوان ورودی دریافت کرده و از تابع سیگموئید برای تبدیل خروجی به مقداری احتمالاتی استفاده می‌کند. نمودار رگرسیون لجستیک شبیه به حرف s زبان انگلیسی است:

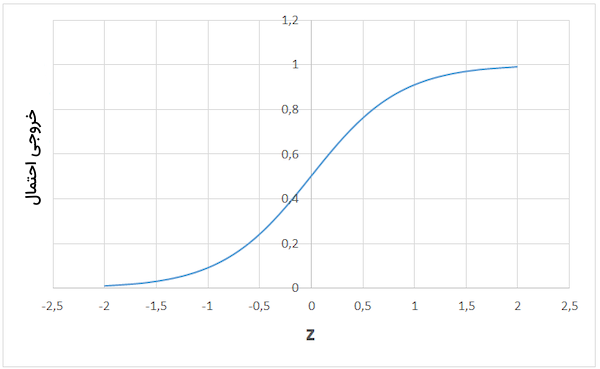
خروجی تابع لجستیک می‌تواند احتمال اسپم بودن ۹۵ درصدی ایمیل یا احتمال ۷۰ درصدی کلیک کردن کاربر بر روی یک تبلیغ باشد. با این حال، در بیشتر اوقات از احتمالات برای دسته‌بندی نقاط داده استفاده می‌شود. اگر احتمال بیشتر از ۵۰ درصد باشد، یعنی نمونه داده متعلق به کلاس مثبت یا همان ۱ بوده و در غیر این‌صورت در کلاس منفی یا ۰ جای می‌گیرد.

الگوریتم K-نزدیک‌ترین همسایه

روش «K-نزدیک‌ترین همسایه» (K-Nearest Neighbors | KNN) از جمله انواع الگوریتم های یادگیری نظارت شده است که هم در مسائل دسته‌بندی و هم رگرسیون کاربرد دارد. ایده اصلی الگوریتم KNN در تخصیص مقدار یا کلاس یک نمونه داده نسبت به دیگر نمونه‌های اطراف آن خلاصه می‌شود. دسته‌بند KNN، کلاس نقاط داده مختلف را از طریق «قاعده رای حداکثری» (Majority Voting Principle) مشخص می‌کند. به عنوان مثال، اگر مقدار k برابر با ۵ باشد، یعنی کلاسِ ۵ مورد از نزدیک‌ترین نقاط داده بررسی شده و کلاسی با بیشترین نمونه به عنوان پیش‌بینی نهایی انتخاب می‌شود. به‌طور مشابه، در مسائل رگرسیون نیز مقدار میانگین ۵ مورد از نزدیک‌ترین نمونه‌ها محاسبه می‌شود. مثال زیر را با ۴ کلاس مختلف در نظر بگیرید:

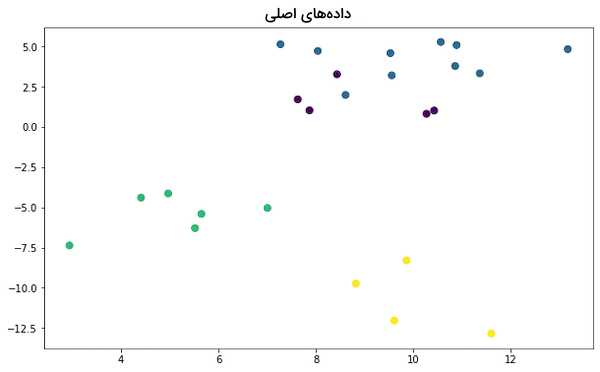
ملاحظه می‌کنید که چگونه با تغییر مقدار k، کلاس پیش‌بینی شده نیز تغییر می‌کند:

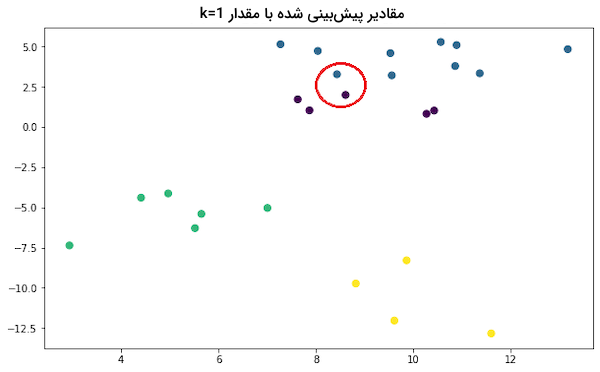
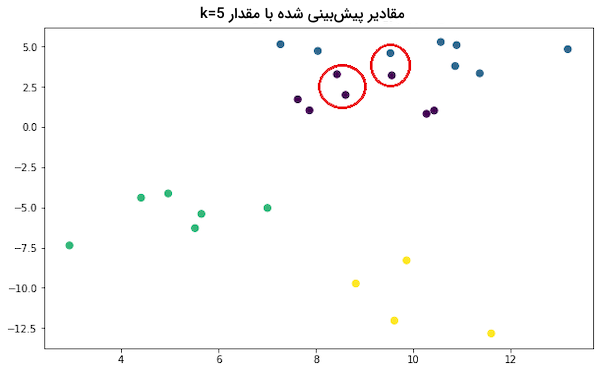
انتخاب بهینه مقدار k از اهمیت بالایی برخوردار است. اگر k بیش از حد کم باشد، مدل وابستگی زیادی به داده‌های آموزشی پیدا کرده و نمی‌تواند عملکرد خود را به نمونه‌های جدید تعمیم دهد و حساسیت زیادی نسبت به نویز و اختلال پیدا می‌کنید. در نتیجه، دقت مدل نسبت به مجموعه آموزشی بالا بوده اما در شناسایی نمونه‌های جدید و از پیش دیده نشده ناتوان و به اصطلاح «بیش‌برازش» (Overfit) شده است. از طرفی دیگر اگر k بیش از حد زیاد باشد، مدل گمراه شده و نسبت به هیچ‌یک از مجموعه‌ها چه آموزشی و چه آزمون، عملکرد قابل قبولی نخواهد داشت. چنین مدلی به اصطلاح «کم‌برازش» (Underfit) شده است.

الگوریتم درخت تصمیم

ایده الگوریتم «درخت تصمیم» (Decision Tree) از طرح پرسش‌های مکرر برای دسته‌بندی داده‌ها سرچشمه می‌گیرد. با مصورسازی مثال نرخ ریزش مشتری، درک بهتری از نحوه کارکرد درخت تصمیم به‌دست می‌آوریم:

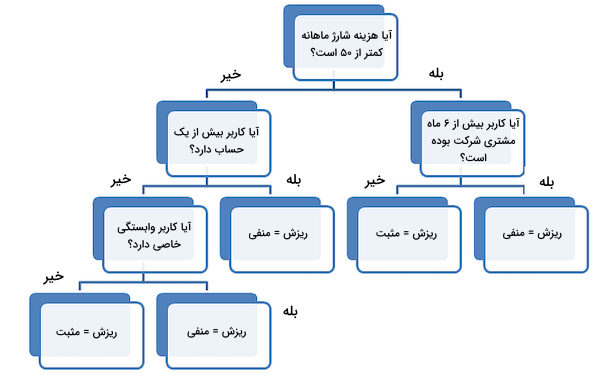
تقسیم اول بر اساس مقدار شارژ ماهانه انجام شده و سپس الگوریتم برای تقسیم‌بندی بیشتر، پرسش‌های دیگری مطرح می‌کند. همزمان با افزایش عمق درخت، پرسش‌ها نیز جزئی‌تر می‌شوند. این‌که در هر مرحله چه پرسش‌هایی عنوان شود، قسمتی مهم و تاثیرگذار در عملکرد درخت تصمیم است. فرض کنید دامنه ویژگی A در مجموعه‌داده شما بین ۰ تا ۱۰۰ است، اما اغلب نمونه‌ها مقداری بیش از ۹۰ دارند. در این صورت، اولین پرسشی که مطرح می‌شود چیزی است شبیه به: «آیا ویژگی A مقداری بیشتر از ۹۰ دارد؟». اگر در پرسش، مقدار را برابر با عددی مانند ۵۰ قرار دهیم، اطلاعات چندانی به‌دست نمی‌آوریم. هدف ما، افزایش قابلیت «پیش‌بینی‌پذیری» (Predictiveness) در هر مرحله و به گونه‌ایست که به‌طور پیوسته، به اطلاعات مدل یادگیری ماشین درباره مجموعه‌داده افزوده شود.

اغلب، تقسیم تصادفی ویژگی‌ها درک ارزشمندی از داده‌ها در اختیار ما نمی‌گذارد. بلکه تقسیم‌هایی ارزشمند هستند که باعث افزایش «خلوص» (Purity) گره‌ها شوند. میزان خلوص گره‌ها نسبت معکوسی با توزیع کلاس‌های مختلف در آن گره دارد. به همین خاطر در هر مرحله، تنها پرسش‌هایی مطرح می‌شوند که درصد خلوص را افزایش یا «ناخالصی» (Impurity) را کاهش دهند. اما چند سوال باید پرسیده شود؟ چه زمان باید این روند متوقف شود؟ چه زمان درخت دیگر به حدی کارآمد شده است که قادر به دسته‌بندی مناسب باشد؟ پاسخ تمامی این پرسش‌ها، به یکی از مهم‌ترین مفاهیم یادگیری ماشین، یعنی بیش‌برازش برمی‌گردد. مدل می‌تواند تا جایی به طرح پرسش ادامه دهد که همه گره‌ها به اصطلاح خالص شده و تنها از یک کلاس باشند.

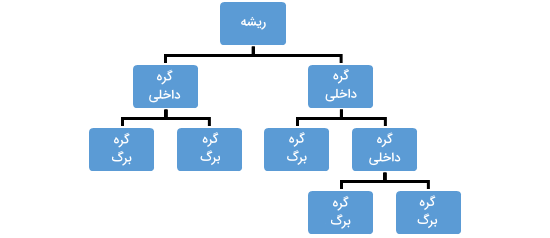
مدل یادگیری ماشین تا جایی روند تقسیم داده‌ها را ادامه می‌دهد که تمامی گره‌های «برگ» (Leaf Nodes) خالص شده باشند. اما باید توجه داشت که چنین مدلی بیش از حد منحصربه‌فرد بوده و قابلیت تعمیم یا «عمومی‌سازی» (Generalization) مناسبی ندارد. مدلی که در تشخیص نمونه‌های آموزشی بسیار توانمند است اما عملکرد قابل قبولی در دسته‌بندی کارآمد داد‌های جدید نشان نمی‌دهد.

الگوریتم جنگل تصادفی

ترکیب چند درخت تصمیم مختلف، الگوریتم «جنگل تصادفی» (Random Forests) را تشکیل می‌دهند. جنگل تصادفی از جمله الگوریتم های یادگیری نظارت شده است که از طریق روشی به‌نام Bagging پیاده‌سازی می‌شود. در این روش، هر درخت تصمیم به‌شکل موازی تخمینی از خروجی ارائه می‌دهد. زمانی که از این الگوریتم در مسائل دسته‌بندی استفاده شود، نتیجه برابر با تخمین درخت تصمیمی خواهد بود که بیشترین رای را آورده است. برای مسائل رگرسیون، پیش‌بینی هر گره برگ از میانگین نتایج تمامی درخت‌های تصمیم تشکیل می‌شود.

الگوریتم جنگل تصادفی با کاهش شانس بیش‌برازش، میانگین دقت را نسبت به روش درخت تصادفی افزایش می‌دهد. همچنین برای رفع مشکل زمان، درخت‌های جنگل تصادفی در موازات یک‌دیگر اجرا می‌شوند. استفاده از درخت‌های تصمیم «ناهمبسته» (Uncorrelated) تاثیر زیادی بر موفقیت جنگل تصادفی دارد. اگر درخت‌ها شبیه به یک‌دیگر باشند، نتیجه نهایی نیز مشابه عملکرد الگوریتم درخت تصمیم خواهد بود. فرایند انتخاب درخت‌های تصمیم ناهمبسته در جنگل تصادفی از طریق دو روش «بوت استرپ» (Bootstrapping) و «غربال ویژگی» (Feature Randomness) حاصل می‌شود:

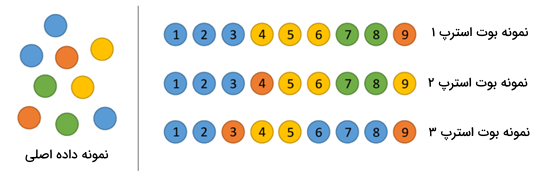
• روش بوت استرپ: تعدادی از نمونه‌ها به شکل تصادفی از مجموعه‌ آموزشی انتخاب شده و جایگذاری می‌شوند. داده‌هایی که «نمونه‌های بوت استرپ» (Bootstrap Samples) نام دارند.

• روش غربال ویژگی: در این روش، از هر درخت تصمیم در جنگل تصادفی، تعدادی از ویژگی‌ها به‌طور تصادفی انتخاب می‌شوند. تعداد ویژگی‌های انتخابی از هر درختِ جنگل تصادفی به‌واسطه پارامتری به‌نام max_features تعیین می‌شود.

نمونه‌های بوت استرپ و غربال ویژگی، امکان استفاده از درخت‌های ناهمبسته را برای جنگل تصادفی مهیا می‌کنند.

الگوریتم درخت تصمیم تقویت شده با گرادیان

الگوریتم درخت تصمیم تقویت شده با گرادیان یا به اصطلاح GBDT، از روشی موسوم به Boosting برای ترکیب چند درخت تصمیم استفاده می‌کند. در روش Boosting، به‌منظور ایجاد «یادگیرنده‌ای قوی» (Strong Learner)، چند «یادگیرنده ضعیف» (Weak Learner) به‌صورت ترتیبی به یک‌دیگر متصل می‌شوند. یادگیرنده‌های ضعیف در الگوریتم GBDT، در واقع همان درخت‌های تصمیم هستند. هر درخت تلاش می‌کند تا خطای درخت قبلی را کمینه کند. در حالی‌که درخت‌ها نقش یادگیرنده‌های ضعیف را ایفا می‌کنند، اضافه شدن درخت‌های بیشتر و متمرکز شدن هر کدام بر خطاهای درخت قبلی، روش Boosting را به مدلی دقیق و کارآمد تبدیل می‌کند. برخلاف تکنیک Bagging، در این روش خبری از نمونه‌های بوت استرپ نیست.

پس از اضافه شدن درختی جدید به مجموعه درخت‌ها، مدل نسبت به نسخه‌ای تغییریافته از مجموعه‌داده اولیه برازش می‌شود. به‌خاطر ترتیبی بودن روند اضافه شدن درخت‌ها، الگوریتم های یادگیری نظارت شده Boosting سرعت پایینی دارند. به‌طور معمول عملکرد چنین مدل‌هایی در «یادگیری آماری» (Statistical Learning) بهتر است.

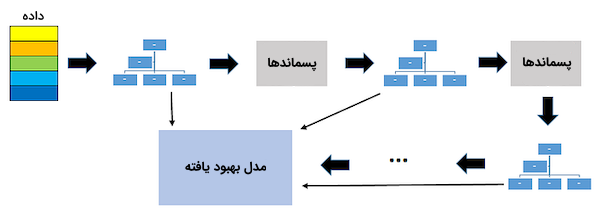
شیوه ترکیب یادگیرنده‌های ضعیف در این الگوریتم به گونه‌ایست که هر یادگیرنده جدید، با برازش نمونه‌های به اشتباه دسته‌بندی شده یا همان «پسماندها» (Residuals)، عملکرد مدل را بهبود می‌بخشد. سپس مدل نهایی، خروجی‌های به‌دست آمده را در هر مرحله باهم جمع کرده و یک یادگیرنده قوی را نتیجه می‌دهد. شناسایی پسماندها بر عهده یک «تابع زیان» (Loss Function) است. به عنوان مثال، تابع «میانگین مربعات خطا» (Mean Squared Error | MSE) در مسائل رگرسیون و تابع «زیان لگاریتمی» (Log Loss) در مسائل دسته‌بندی کاربرد دارد. باید توجه داشت که با اضافه شدن درخت‌های جدید، سایر درخت‌ها تغییر نمی‌کنند، بلکه این درخت جدید است که نسبت به پسماندهای مدل فعلی برازش می‌شود. تا به امروز نسخه‌های بهبود یافته مختلفی مانند XGBOOST، LightGBM و CatBoost بر پایه الگوریتم GBDT پیاده‌سازی شده‌اند.

جمع‌بندی

الگوریتم های یادگیری نظارت شده طیف گسترده‌ای از روش‌ها با اهداف مشترک را شامل می‌شوند. شاید راه‌حل مسئله در یادگیری نظارت شده برای داده‌های جدید شناخته شده نباشد اما، الگوهایی در مجموعه‌داده قابل شناسایی است که به پیش‌بینی موثر خروجی مدل یادگیری ماشین کمک می‌کنند. در این مطلب از مجله فرادرس، با مفهوم یادگیری نظارت شده آشنا شدیم و انواع الگوریتم‌های رایج آن را معرفی کردیم. الگوریتم های یادگیری نظارت شده نقش مهمی در پیشرفت‌های آینده حوزه هوش مصنوعی و کاربردهایی همچون علم داده ایفا می‌کنند.