در دنیای الکترونیک، خازنها به عنوان اجزای رایج و ضروری شناخته میشوند و در کاربردهای مختلف نقش اساسی دارند. این اجزا ساده و در عین حال بسیار مهم، توانایی شگفت انگیزی در ذخیره و آزاد سازی انرژی الکتریکی دارند که آنها را قادر میسازد طیف وسیعی از وظایف را انجام دهند. در این مطلب به بررسی کامل خازن چیست و اجرا آن و همینطور انواع خازن و کاربرد آن با مثال پرداخته خواهد شد بنابراین برای درک کامل ماهیت خازن و کاربرد آن این مطلب در مجله فرادرس را تا آخر مطالعه کنید.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
خازن چیست؟
در این بخش به توضیح ماهیت خازن و اجزای اصلی آن میپردازیم همچنین نحوه کار خازن بررسی خواهد شد.
معرفی خازن
«خازن» (Capacitor) یک عضو مهم در صنایع الکترونیک است. وظیفه اصلی خازن ذخیره انرژی الکتریکی است. وقتی که دو سر یک خازن را به یک اختلاف پتانسیل وصل میکنید بار الکتریکی را در صفحات خود ذخیره میکند و در صورت نیاز آن را به مدار بازمیگرداند. گرچه خازنها انواع و شکلهای مختلفی دارند اما اصول کار آنها یکسان است.
اجزای اصلی خازن چیست؟
سادهترین نوع خازن از دو صفحه رسانا که هماندازه و موازی با یکدیگر هستند و فاصله اندکی بین آنها وجود دارد، تشکیل شدهاند. برای درک بهتر به شکل زیر توجه کنید:
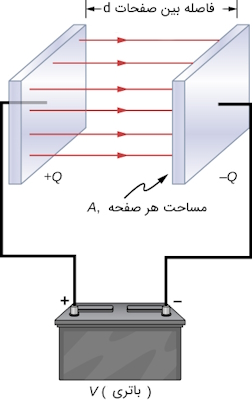
ظرفیت یک خازن مسطح متناسب با اجزا آن به صورت زیر است:
$$C= varepsilon _{0} dfrac{A}{d} $$
عوامل به کار رفته در رابطه فوق به شرح زیر است:
- $$C$$ : ظرفیت خازن.
- $$epsilon_0$$ : ثابت گذردهی.
- $$A$$ : مساحت یکی از صفحات خازن.
- $$d$$ : فاصله بین صفحات خازن
در ادامه این مطلب این رابطه را اثبات خواهیم کرد.
فضای بین صفحات خازن معمولا خالی است اما خازنهایی هستند که یک ماده عایق بنابر کاربرد خاص، بین صفحات خازن قرار میگیرد که آن را به اصطلاح دیالکتریک میگویند. در بخشهای بعدی دیالکتریک را بیشتر معرفی خواهیم کزد.
خازن چگونه کار میکند؟
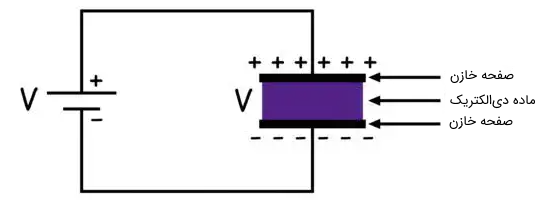
مطابق شکل زیر، وقتی اختلاف پتانسیل به خازن متصل میشود آن صفحه خازن که به پایه مثبت منبع تغذیه متصل است دارای بار مثبت میشود و صفحه دیگر که به پایه منفی منبع تغذیه متصل است دارای بار منفی میشود. اگر ماده دیالکتریک در خازن باشد مانع انتقال بارهای الکتریکی بین صفحات خازن میشود.
شارژ خازن
وقتی خازن به اصطلاح شارژ میشود یک اختلاف پتانسیل در دو سر صفحات خازن به وجود میآید و این اختلاف پتانسیل به صورت نمایی افزایش پیدا میکند تا هنگامی که برابر اختلاف پتانسیل منبع تغذیه شود.
تخلیه خازن
اگر بارهای خازن شارژ شدهای را تخلیه کنیم به اصطلاح «دشارژ» خازن گفته میشود.
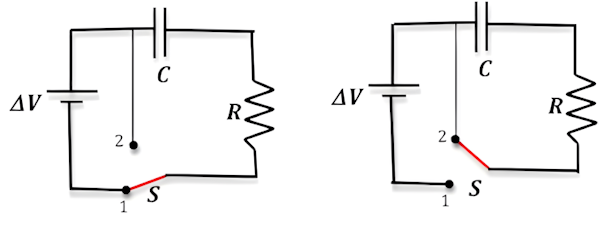
در شکل فوق که یک مدار با منبع تغذیه مستقیم و یک خازن و مقاومت در آن وجود دارد. در شکل چپ که کلید S در حالت ۱ قرار دارد، باتری در مدار متصل است و خازن در حال شارژ شدن است. در شکل راست که کلید S در حالت ۲ قرار داده شده است، اتصال باتری در مدار قطع میشود و در نتیجه بارهای خازن به وسیله مقاومت تخلیه «دشارژ» میشود.
انواع خازن چیست؟
در قسمت قبل ماهیت خازن و نحوه عملکرد کلی آن را توضیح دادیم، در این بخش انواع دستهبندی خازن را معرفی خواهیم کرد. دستهبندهای متفاوتی برای خازن وجود دارد که در اینجا به معرفی اجمالی رایجترین آنها میپردازیم.
- شکل ساختاری
- دیالکتریک
- ظرفیت
- قطبش
- کاربرد
شکل ساختاری
ذخیرهسازی انرژی الکتریکی که کار اصلی خازن است به شکل ساختاری و اجزا خازن مانند؛ اندازه و جنس صفحات، فاصله آنها از یکدیگر و همچنین اندازه و جنس دیالکتریک بستگی دارد. خازنها را از نظر شکل ساختاری میتوان به انواع زیر دستهبندی کرد:
- خازن مسطح
- خازن استوانهای
- خازن کروی
- خازن رول شده
در ادامه این مطلب به معرفی بیشتر آنها پرداخته خواهد شد.
دی الکتریک
ظرفیت خازن با مساحت صفحات رابطه مستقیم و با فاصله آنها از هم رابطه معکوس دارد. اگر بخواهیم ظرفیت یک خازن را افزایش دهیم باید مساحت صفحات خازن را افزایش دهیم یا فاصله بین صفحات را کاهش دهیم یا ترکیبی از هر دوی آنها اما این کار از جایی به بعد باعث سوختن خازن میشود در نتیجه یک ماده عایق به نام دیالکتریک را بین صفحات خازن قرار میدهند تا هم ظرفیت خازن افزایش پیدا کند و هم باعث عدم سوختن آن شود.
در رابطه ظرفیت خازنهایی که دیالکتریک دارند ثابت دیالکتریک ($$kappa$$) اضافه میشود در نتیجه رابطه ظرفیت خازن مسطح به شکل زیر خواهد بود:
$$C=kappa varepsilon _{0} dfrac{A}{d} $$
انواع دیالکتریکها به همراه مقدار ثابت $$kappa$$ و قدرت دیالکتریک در جدول زیر به صورت اجمالی آمده است و در انتهای مطلب جدول کامل قرار دارد.
| ماده | ثابت دیالکتریک ($$kappa$$) | قدرت دیالکتریک ($$V/m$$) |
| «خلا» (Vacuum) | 1.00000 | — |
| «هوا» (Air) | 1.00059 | $$3 times 10^{6}$$ |
| «تفلون» (Teflon) | 2.1 | $$60 times 10^{6}$$ |
توجه کنید که ثابت دیالکتریک هوا بسیار به ثابت دیالکتریک خلا نزدیک است اما تفاوت آنها در این است که اگر میدان الکتریکی (برای خازن مسطح $$E=V/d$$) خیلی بزرگ شود، هوا به رسانا تبدیل میشود. همچنین در جدول فوق قدرت دیالکتریک مواد مختلف با واحد ولت بر متر آورده شده است.
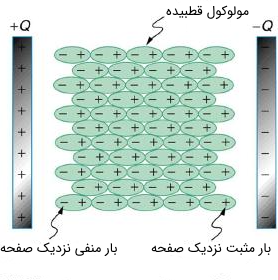
قطبیدگی مولکولهای دیالکتریک
قطبیدگی عایق دلیل افزایش ظرفیت خازن در استفاده از دیالکتریک از دیدگاه میکروسکوپیک است. در واقع هر چقدر راحتتر دیالکتریک قطبیده شود ضریب ثابت دیالکتریک یعنی $$kappa$$ نیز بیشتر میشود. برای مثال آب یک مولکول قطبی است به دلیل آنکه یک سمت آن مثبت و سمت دیگر آن منفی است. قطبیدگی آب باعث شده که ضریب دیالکتریک آن به بزرگی ۸۰ باشد. بهترین راه توصیف قطبیدگی به وسیله نیروی کولنی است.
همانطور که در شکل زیر ملاحظه میکنید، مولکولهای ماده دیالکتریک که بین صفحات خازن قرار دارند بارهای آنها از هم جدا شدهاند. نیروی کولنی بین صفحه باردار خازن و نزدیکترین سر مولکول ماده دیالکتریک بسیار قوی است. به دلیل اینکه آنها بسیار به هم نزدیک هستند، بارهای بیشتری جذب صفحه خازن میشود.
میدان الکتریکی در دیالکتریک
روش دیگری که باعث توجیه افزایش ظرفیت خازن به وسیله دیالکتریک میشود، میدان الکتریکی درون خازن است. در شکل زیر یک خازن با دیالکتریک با خطوط میدان الکتریکی درون آن را میبینید.
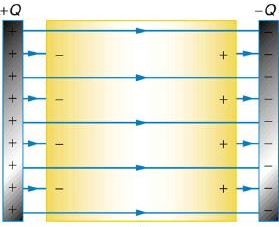
از آنجایی که خطوط میدان در دیالکتریک به بارهای موجود در آن ختم میشوند، تعداد کمتری از آنها از یک طرف خازن به طرف دیگر میروند. بنابراین، شدت میدان الکتریکی کمتر از آن چیزی است که اگر بین صفحات خلا وجود داشت، حتی اگر همان مقدار بار روی صفحات وجود داشته باشد. رابطه ولتاژ بین صفحات خازن به صورت زیر است:
$$V=Ed$$
اگر میدان الکتریکی کاهش پیدا کند، ولتاژ هم کاهش پیدا میکند. همچنین از رابطه ظرفیت خازن $$C=Q/V$$ چون ولتاژ با ظرفیت خازن رابطه معکوس دارد بنابراین هر چه ولتاژ کاهش پیدا کند، ظرفیت خازن افزایش پیدا میکند.
خازنها میتوان براساس ماده دیالکتریک دستهبندی کرد.
ظرفیت
دستهبندی خازن براساس ظرفیت به دو گروه ظرفیت ثابت و متغیر تقسیم میشوند. از جمله خازنهایی که ظرفیت ثابت دارند میتوان به خازنهای سرامیکی، الکترولیتی، فیلم و خازنهایی که دیالکتریک آنها هوا یا خلا است را نام برد. خازنهایی که ظرفیت متغیر دارند دارای صفحات متحرک هستند که بین صفحات ثابت قابلیت حرکت دارند.
قطبش
نوع دیگری از دستهبندی خازنها براساس قطبیدگی آنها است. خازنهایی که ناقطبی هستند قرارگیری پایههای آنها در مدار هیچ تفاوتی ندارد ولی خازنهایی که قطبی هستند حتما باید پایه آنها منطبق با علامت ولتاژ منبع تغذیه باشد.
کاربرد
انتخاب خازن معمولا به کاربرد مدار بستگی اساس دارد. اینکه خازن چگونه در مدار استفاده شود و چه عملکردی داشته باشد نقش تعیین کنندهای دارد. بعضی خازنها عملکرد بهتری نسبت به سایر خازنها در برخی مدارها دارند. انتخاب درست خازن در طراحی مدار بسیار حائز اهمیت است.
کاربردهای خازن چیست؟
خازنها میتوانند برای کاربردهای متفاوتی در مدارها مورد استفاده قرار گیرند. اگرچه اساس کار آنها یکسان است ولی مشخصههای خازن تنوع زیادی در آنها ایجاد کرده است. در این قسمت به معرفی کاربردهای خازن از جمله ذخیره و آزادسازی انرژی، صاف کردن سیگنال، جفت کردن سیگنال، تجزیه سیگنال و هماهنگسازی پرداخته خواهد شد. مدارهای مختلف، خازنهایی با ویژگیها و مشخصههای متفاوتی از جمله جریان، ولتاژ، ظرفیت، دمای کار و غیره نیاز دارند.
ذخیره و آزادسازی انرژی
در این مورد خاص، خازن میتواند بار را در خود ذخیره کند و به مدت کوتاهی به عنوان منبع تغذیه عمل کند. برای مثال ابرخازنها با ظرفیت چندین فاراد نسبت به باتریهای قابل شارژ ارزانتر هستند و طول عمر بیشتری دارند البته حداکثر ولتاژ خروجی آنها محدود است.
صاف کردن سیگنال
این همان خازن تجزیه (Decoupling) است، خازن صاف کننده معمولا در ارتباط با مدارها و سیستم های منبع تغذیه استفاده میشود. وقتی که یک منبع تغذیه یا سیگنال خطی از یک ترانسفورماتور و یکسوکننده عبور میکند، موج سیگنال خروجی صاف نیست و بین صفر و حداکثر ولتاژ متغیر است و شکل آن به صورت موجهای نیمسینوسی هست که اگر به طور مستقیم به مدار وصل شود ناکارآمد خواهد بود درحالی که مدار به جریان مستقیم نیاز دارد. برای حل این مشکل یک خازن تفکیک کننده یا صاف کننده ولتاژ خروجی در مدار قرار میدهند.
در این کاربرد، با به حداکثر رسیدن ولتاژ خروجی خازن شارژ میشود و زمانی که ولتاژ یکسو کننده به کمتر از ولتاژ خازن برسد آنگاه خازن تخلیه میشود. به طور معمول خازن با ظرفیت زیادی برای تامین این جریان مورد نیاز است در نتیجه خازنهای الکترولیتی مناسبترین گزینه برای این نوع کاربرد هستند.

جفت کردن سیگنال (Coupling)
در این کاربرد خازن در مدار فقط اجازه عبور سیگنال متناوب در یک قسمت از مدار را میدهد و سیگنال مستقیم را مسدود میکند. این کاربرد خازن معمولا در متصل کردن دو پایه یک تقویتکننده (Amplifier) استفاده میشود. ظرفیت خازن در اینجا اهمیتی ندارد بلکه راکتانس پایین خازن مهم است.
تجزیه سیگنال (Decoupling)
خازن تجزیه، یک قسمت از مدار را از بقیه جدا میکند. نویز تولید شده به وسیله سایر اجرا را از بین میبرد. معمولا بین منبع تغذیه و زمین قرار میگیرد. برای فرکانسهای بالاتر نام جایگزین آن، خازن کنارگذر است بخاطر اینکه یک میانبر از منبع تغذیه یا سایر اجزا مدار با امپدانس بالا است.
هماهنگسازی و زمانبندی
در این کاربرد خازن با یک مقاومت یا یک القاگر در یک رزونانس یا مدار وابسته به زمان مورد استفاده قرار میگیرد. در اینجا خازن ممکن است در مدار فیلتر، نوسانگر تنظیم شده یا در یک عنصر زمانبندی برای مدار الکترونیکی مانند a-stable ظاهر شود. زمان لازم برای شارژ و تخلیه خازن، تعیین کننده عملکرد مدار است. در این کاربرد خازن، دقت مهم است بنابراین مقاومت اولیه و پایداری دما خازن برای اطمینان از عملکرد آن در فرکانس مورد نظر مهم است. خازنهایی با دیالکتریک سرامیکی، فیلم پلاستیکی و نقره-میکا مورد استفاده در این کار هستند.
مشخصات خازن چیست؟
در این بخش به معرفی مشخصات اصلی خازنها مانند ظرفیت، ولتاژ، جریان، دما و غیره میپردازیم که در همه انواع خازنها مشترک هستند.
ظرفیت خازن
ظزفیت خازن عبارت است از باز ذخیره شده در خازن به ازای یک ولت اختلاف پتانسیل که این رابطه را به صورت زیر مینویسیم:
$$Q=C times V$$
عناصر رابطه فوق عبارتند از:
- Q: بار الکتریکی که واحد آن کولن است.
- C: ظرفیت خازن که واحد آن فاراد است.
- V: اختلاف پتانسیل که واحد آن ولت است.
ظرفیت خازن را با C نمایش میدهند و واحد اندازهگیری آن فاراد است. مهمترین مشخصه خازن، ظرفیت آن است. ظرفیت خازن میتواند با تغییر فرکانس عوض شود که با تغییر دما نیز همراه است. خازنهای سرامیکی کوچک میتوانند ظرفیتی تا اندازه ۱ پیکوفاراد داشته باشند در حالی که ظرفیت خازنهای بزرگ الکترولیتی میتواند تا ۱ فاراد باشد.
ولتاژ خازن
ولتاژ کاری یکی دیگر از مشخصههای مهم خازن است که عبارت است از بیشترین ولتاژ پیوسته قابل تحمل که از منبع با جریان مستقیم یا متناوب که از خازن عبور میکند نامیده میشود که معمولا ولتاژ مستقیم را روی بدنه خازن درج میکنند.
مقدار ولتاژ مستقیم و متناوب خازن یکسان نیست. منظور از ولتاژ متناوب در خازن، ولتاژ موثر (R.M.S) است درحالی که حداکثر یا اوج ولتاژ به مقدار 1.414 از آن بزرگتر است. همینطور مقدار ولتاژ مستقیم درج شده روی خازن مربوط به کار کردن آن در محدوده دمای ۳۰- تا ۷۰+ درجه سانتیگراد است. ولتاژ مستقیم یا متناوب بیش از حد باعث از بین رفتن خازن میشود و اگر خازن در محدوده مشخص شده ولتاژ و دمای پایین کار کند باعث افزایش عمر آن میشود.
جریان نشتی خازن
دیالکتریکی که در داخل خازن برای جدا کردن صفحات رسانا استفاده میشود یک عایق کامل نیست، در نتیجه یک جریان بسیار کوچک (نشتی) از طریق دیالکتریک جریان مییابد. این به دلیل تأثیر میدانهای الکتریکی قدرتمندی است که توسط بار روی صفحات رسانا هنگامی که ولتاژ منبع ثابت اعمال میشود، ایجاد میکند. این جریان مستقیم که در محدوده نانو آمپر (nA) قرار دارد را جریان نشتی خازن گویند. نشت جریان نتیجه عبور فیزیکی الکترونها از طریق محیط دیالکتریک در اطراف لبههای آن است و اگر ولتاژ منبع قطع شود، به مرور خازن را به طور کامل تخلیه میکند. اگر نشتی بسیار کم باشد مانند خازن با دیالکتریک فیلم یا فویل به آن مقاومت عایق گویند ($$R_{p}$$) و میتوان مانند شکل زیر آن را مثل یک مقاومت مجزا به صورت موازی با خازن نشان داد.
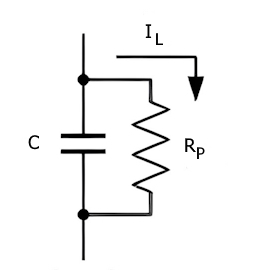
نشتی جریان در خازن با دیالکتریک الکترولیتی زیاد است به طوری که جریان الکترونها مستقیم از ماده دیالکتریک عبور میکند (در مرتبه ۵ تا ۲۰ میکروآمپر به ازای هر میکروفاراد). همچنین نشتی جریان در خازن با دیالکتریک الکترولیتی آلومینیوم با افزایش دما، زیاد میشود. نشت جریان خازن یک عامل مهم در تقویت کننده جفتشده یا مدارهای منبع تغذیه است. بهترین انتخاب خازن برای کاربرد جفت کردن سیگنال و ذخیرهسازی انرژی از نوع دیالکتریک با تفلون و سایر مواد پلاستیکی است زیرا در آنها ضریب دیالکتریک کمتر موجب مقاومت عایق بیشتری میشود.
قطبیدگی
قطبیدگی خازن معمولا به خازنها از نوع الکترولیت به خصوص نوع آلومینیومی آن اطلاق میشود. خازنهای الکترولیتی قطبیده هستند به این علت که پایههای خازن باید کاملا منطبق بر علامت ولتاژ منبع تغذیه باشد. اگر پایههای خازن قطبیده را اشتباه در مدار قرار دهیم باعث از بین رفتن لایه اکسید شده در خازن و در نتیجه سوختن آن خواهیم شد.
دما
تغییرات دما در اطراف خازن بر مقدار ظرفیت خازن تأثیر میگذارد زیرا خواص دیالکتریک تغییر میکند. اگر دمای محیط اطراف خازن بیش از حد گرم یا سرد شود، مقدار ظرفیت خازن ممکن است به اندازهای تغییر کند که عملکرد صحیح مدار را تحت تاثیر قرار دهد. دمای کاری معمول برای اکثر خازنها با ولتاژ معین بین ۳۰- تا ۱۲۵+ درجه سانتیگراد است ولی دما برای خازن با دیالکتریک پلاستیکی نباید بیشتر از ۷۰+ درجه سانتیگراد شود.
تلورانس
مانند مقاومتها، خازنها نیز دارای یک مقاومت درونی یا تلورانس (Tolerance) هستند که با نماد مثبت و منفی نمایش داده میشوند که برای خازنها با ظرفیت کم به شکل (pF±) و برای خازنها با ظرفیت بالا به صورت (%±) نمایش میدهند. تلورانس به معنی میزان تغییر مجاز ظرفیت اسمی خازن است و معمولا بین $$-20٪$$ تا $$+80٪$$ میتواند باشد. برای مثال یک خازن که ظرفیت اسمی آن ۱۰۰ میکروفاراد با تلورانس $$pm20٪$$ است میتواند ظرفیت عملی در محدوده $$80mu F$$ تا $$120mu F$$ داشته باشد.
نماد خازن و نمایش آن
حال که با اجزا و کاربرد خازن چیست آشنا شدید در این بخش نماد شماتیک خازن در مدار را معرفی خواهیم کرد.
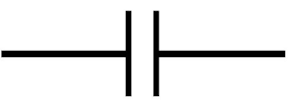
در شکل فوق نماد یک خازن ساده در مدار را مشاهده میکنید. به خطوط موازی توجه کنید که نشانگر صفحات هماندازه و موازی در خازن است.
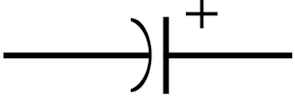
در شکل بالا نماد یک خازن قطبی الکترولیتی را میبینید. به دلیل اهمیت قطبیدگی، پایه مثبت خازن در سمت راست و قسمت منحنی در چپ نشاندهنده پایه منفی خازن است.
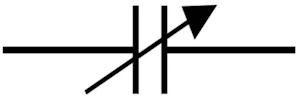
در شکل فوق یک خازن با ظرفیت متغیر نشان داده شده است.
محاسبات مربوط به خازن
اکنون که با مفهوم خازن چیست و چه کاربردی دارد آشنا شدید، در این بخش به محاسبه ظرفیت خازن براساس ساختارهای متفاوت، انرژی ذخیره شده در خازن، خازن معادل در مدار با مثال پرداخته خواهد شد.
بهمنظور یافتن ظرفیت خازن، در ابتدا باید میدان الکتریکی بین دو صفحه را تحلیل کنیم. توجه داشته باشید که یک خازن واقعی دارای اندازهای محدود است. بنابراین خطوط میدان الکتریکی در لبه آن به صورت خط راست نخواهند بود. در حقیقت میدان الکتریکی را نمیتوان در نزدیکی لبه صفحات فقط به صورت خطوط راست تصور کرد. به این پدیده «اثر لبه» (Edge Effect) گفته میشود. در شکل زیر نیز مشاهده میکنید که میدان الکتریکی در نزدیکی لبه به صورت منحنی در آمده است. این انحنا همان اثر لبه را نشان میدهد.
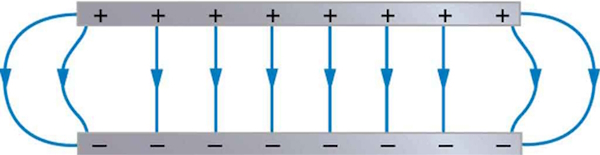
به دلیل اینکه فاصله بین صفحات خازن بسیار کم است بنابراین میتوان برای بدست آوردن ظرفیت خازن اثر لبه را نادیده بگیریم و خطوط میدان الکتریکی بین صفحات خازن را فقط خطوط صاف در نظر بگیریم.
خازن مسطح
چگالی بار سطحی را به صورت زیر تعریف میکنیم:
$$sigma = frac{Q}{A}.$$
که در رابطه فوق $$sigma$$، نماد چگالی بار سطحی است.
رابطه میدان الکتریکی به شکل زیر است:
$$E = frac{sigma}{epsilon_0},$$
- $$E$$ : میدان الکتریکی یکنواخت بین صفحات خازن
- $$sigma$$ : چگالی بار سطحی
- $$epsilon_0$$ : ثابت گذردهی خلا برابر $$epsilon_0 = 8.85 times 10^{-12}F/m$$
همچنین برای رابطه اختلاف پتانسیل داریم:
$$V = Ed = frac{sigma d}{epsilon_0} = frac{Qd}{epsilon_0A}.$$
برای محاسبه ظرفیت خازن مسطح از رابطه زیر استفاده میکنیم:
$$C = frac{Q}{V} = frac{Q}{Qd/epsilon_0A} = epsilon_0frac{A}{d}. label{eq2}$$
مثال اول خازن مسطح
در این مثال میخواهیم (الف) ظرفیت یک خازن مسطح بدون دیالکتریک که مساحت صفحات آن $$1.00 , m^2$$ و فاصله صفحات آن از هم ۱ میلیمتر است را محاسبه کنیم.
در قسمت (ب) نیز میخواهیم مقدار بار ذخیره شده در خازن که اگر اختلاف پتانسیل آن برابر $$3.00 times 10^3 V$$ باشد را محاسبه میکنیم.
پاسخ:
با استفاده از فرمول کلی که برای ظرفیت خازن مسطح در بالا گفته شد، میتوانیم به آسانی مقادیر داده شده را درون آن جایگذاری کنیم و ظرفیت خازن را حساب کنیم.
$$C = epsilon_0frac{A}{d} = left(8.85 times 10^{-12} frac{F}{m} right) frac{1.00 , m^2}{1.00 times 10^{-3}m} = 8.85 times 10^{-9} F = 8.85 , nF. nonumber$$
برای حل قسمت (ب) نیز از اولین فرمولی که در قسمت ظرفیت خازن معرفی کردیم یعنی $$Q=C times V$$ استفاده میکنیم.
$$Q = CV = (8.85 times 10^{-9}F)(3.00 times 10^3 V) = 26.6 , mu C. nonumber$$
خازن استوانهای
خازن استوانهای مطابق شکل زیر از دو رسانای استوانهای هممرکز تشکیل شده است. استوانه داخلی که با شعاع $$R_1$$ نمایش داده میشود میتوان توخالی یا توپر باشد و استوانه خارجی که با شعاع $$R_2$$ نمایش داده شده است، توخالی است. طول هر دو استوانه داخلی و خارجی برابر $$L$$ فرض میشود همچنین بار جمع شده در استوانه داخلی برابر $$+Q$$ و بار جمع شده در استوانه خارجی برابر $$-Q$$ است.
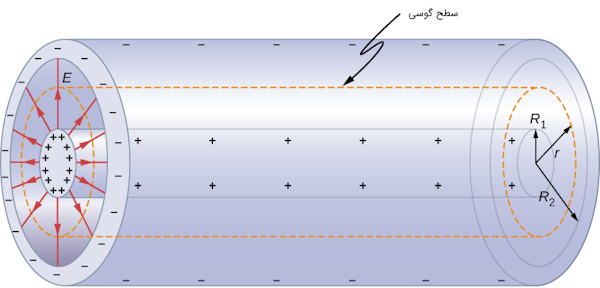
برای محاسبه ظرفیت خازن استوانهای از اثر لبه صرف نظر میکنیم و میدان الکتریکی یکنواخت و به صورت قائم از استوانه داخلی (بار مثبت) به استوانه خارجی (بار منفی) فرض میکنیم. با استفاده از سطحی گوسی بسته S خواهیم داشت:
$$oint_S vec{E} cdot hat{n} dA = E(2pi rl) = frac{Q}{epsilon_0}.$$
بنابراین میدان الکتریکی بین صفحات به صورت زیر است:
$$vec{E} = frac{1}{2pi epsilon_0} frac{Q}{r , l} hat{r}.$$
در اینجا $$hat{r}$$ بردار شعاعی همراستا با شعاع استوانه است. با جایگذاری میدان الکتریکی در رابطه $$V_B – V_A = – int_A^B vec{E} cdot dvec{l}, label{eq0}$$ میتوانیم اختلاف پتانسیل بین دو صفحه استوانه را حساب کنیم.
$$V = int_{R_1}^{R_2} vec{E} cdot dvec{l}_p = frac{Q}{2pi epsilon_0 l} int_{R_1}^{R_2}frac{1}{r} hat{r} cdot (hat{r} , dr) = frac{Q}{2pi epsilon_0 l} int_{R_1}^{R_2}frac{dr}{r} = frac{Q}{2pi epsilon_0 l} ln , r bigg|_{R_1}^{R_2} = frac{Q}{2pi epsilon_0 l} frac{R_2}{R_1}.$$
بنابراین ظرفیت خازن استوانهای به صورت زیر خواهد بود:
$$C = frac{Q}{V} = frac{2pi epsilon_0 , l}{ln(R_2/R_1)}. label{eq10}$$
یک نمونه استفاده رایج از خازن استوانهای، کابلهای هم محور هستند که ظرفیت آن را بر واحد طول محاسبه میکنند. بار الکتریگی بر روی لایه خارجی استوانه داخلی و لایه داخلی استوانه خارجی تجمع میکند. بنابراین ظرفیت بر واحد طول یک کابل هم محور به صورت زیر است:
$$frac{C}{l} = dfrac{2pi epsilon_0}{ln(R_2/R_1)}.$$
مثال اول خازن استوانهای
یک کابل هم محور با شعاع استوانه داخلی 0.28mm و شعاع استوانه خارجی 2.2mm و دیالکتریک پلاستیکی $$epsilon_r = 2.7text{,}$$ داریم. میخواهیم در دو حالت (الف) بدون وجود دیالکتریک و (ب) با دیالکتریک تعریف شده ظرفیت را حساب کنیم.
پاسخ:
با استفاده از رابطهای که برای ظرفیت بر واحد طول کابل هم محور تعریف کردیم، مقادیر داده شده را جایگذاری میکنیم.
$$begin{align*}\&(C/L)_0 = dfrac{2piepsilon_0}{lnleft(R_1/R_2 right)}, \& = dfrac{2pitimes 8.85times 10^{-12}}{lnleft(2.2/0.28right)} = 115 text{ pF/m}. end{align*}$$
اگر دیالکتریک پلاستیکی را قرار دهیم، خواهیم داشت:
$$begin{equation*}C/L = epsilon_r (C/L)_0 = 2.7 times 115 text{ pF/m} = 311 text{ pF/m}.end{equation*}$$
خازن کروی
خازن کروی نوعی از خازن است که شامل دو کره هممرکز به عنوان صفحات خازن است. به شکل زیر توجه کنید.
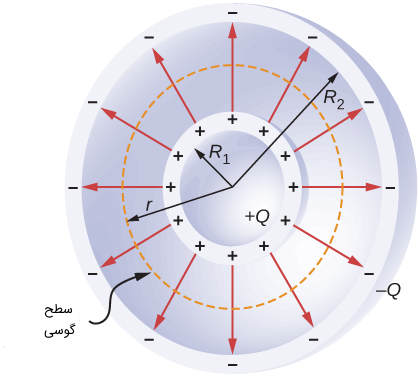
کره داخلی که شعاع آن کوچکتر است $$R_1$$ و کره خارجی که شعاع آن بزرگتر است $$R_2$$، هستند و هر دو صفحات بار مساوی و به ترتیب $$+Q$$ و $$-Q$$ را در زمان شارژ دارند. جهت میدان الکتریکی به صورت متقارن از صفحه داخلی به صفحه خارجی و به صورت قائم است. میتوانیم اندازه میدان الکتریکی را با استفاده از قانون گاوس در مختصات کروی با شعاع r حساب کنیم. بنابراین برای بار $$+Q$$ در سطح بسته S خواهیم داشت:
$$oint_S vec{E} cdot hat{n}dA = E(4pi r^2) = frac{Q}{epsilon_0}.$$
بنابراین میدان الکتریکی بین صفحات به صورت زیر است:
$$vec{E} = frac{1}{4pi epsilon_0} frac{Q}{r^2} hat{r}.$$
میدان الکتریکی را داخل رابطه زیر جایگذاری میکنیم و سپس بین صفحات خازن و در مسیر شعاع r انتگرالگیری میکنیم.
$$V_B – V_A = – int_A^B vec{E} cdot dvec{l}$$
$$V = int_{R_1}^{R_2} vec{E} cdot dvec{l} = int_{R_1}^{R_2} left(frac{1}{4pi epsilon_0} frac{Q}{r^2} hat{r}right) cdot (hat{r} dr) = frac{Q}{4pi epsilon_0}int_{R_1}^{R_2} frac{dr}{r^2} = frac{Q}{4pi epsilon_0}left(frac{1}{R_1} – frac{1}{R_2}right).$$
در این رابطه اختلاف پتانسیل بین صفحات خازن به شکل زیر است:
$$V = -(V_2 – V_1) = V_1 – V_2.$$
با استفاده از رابطه $$C = frac{Q}{V} label{eq1}$$ در نتیجه خواهیم داشت:
$$C = dfrac{Q}{V} = 4pi epsilon_0 frac{R_1R_2}{R_2 – R_1}. label{eq3}$$
مثال اول خازن کروی
میخواهیم ظرفیت یک خازن کروی بدون دیالکتریک که شعاع کره داخلی آن ۱ سانتیمتر و شعاع کره خارجی آن ۲ سانتیمتر است را حساب کنیم.
پاسخ:
با استفاده از رابطه فوق، مقادیر داده شده در مثال را جایگذاری میکنیم.
$$begin{align*}\&C = 4piepsilon_0, left( dfrac{1}{R_{in}} – dfrac{1}{R_text{out}} right)^{-1}\& = 4pitimes 8.85times 10^{-12}, left( dfrac{1}{0.01} – dfrac{1}{{0.02}} right)^{-1}\& = 4pitimes 8.85times 10^{-12}, dfrac{0.01times 0.02}{0.01+0.02} \& = 7.4times 10^{-13}text{ F}. end{align*}$$
مجموعه خازن در مدار
در هر مدار دلخواه، بنابر کاربرد ممکن است چندین خازن وجود داشته باشند که به شیوهای به هم متصل شدهاند. مهمترین و رایجترین نوع اتصال خازن، متوالی (سری) و موازی است. که در ادامه به بررسی هر یک از آنها میپردازیم.
اثبات ظزفیت معادل اتصال متوالی خازن
مطابق شکل زیر اگر سه خازن را به صورت متوالی به یکدیگر وصل کنیم، همه آنها مقدار بار $$Q$$ یکسانی را از منبع تغذیه دریافت خواهند کرد.
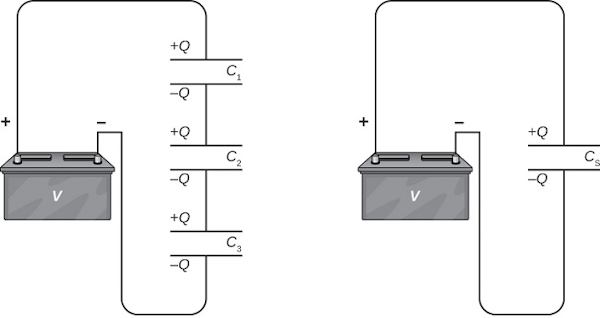
$$Q_{S}=Q_{1}=Q_{2}=Q_{3}$$
اختلاف پتانسیل کل برابر جمع اختلاف پتانسیل هر خازن است.
$$V = V_1 + V_2 + V_3.$$
با استفاده از رابطه اساسی زیر میتوانیم خازنها را با هم جمع کنیم و یک ظرفیت معادل همهی خازنها در مدار داشته باشیم:
$$C=dfrac{Q}{V}.$$
$$dfrac{Q}{C_S} = dfrac{Q}{C_1} + dfrac{Q}{C_2} + dfrac{Q}{C_3}.$$
بنابراین ظرفیت خازن معادل در مدار متوالی به صورت زیر خواهد بود:
$$dfrac{1}{C_S} = dfrac{1}{C_1} + dfrac{1}{C_2} + dfrac{1}{C_3}.$$
مثال اول خازن متوالی
ظرفیت معادل سه خازن $$1.000 mu F$$ و $$5.000 mu F$$ و $$8.000 mu F$$ را که به صورت متوالی در مدار قرار دارند محاسبه میکنیم.
پاسخ:
با استفاده از رابطه خازن معادل میتوانیم به راحتی ظرفیت معادل این سه خازن را حساب کنیم.
$$begin{align*} dfrac{1}{C_S} &= dfrac{1}{C_1} + dfrac{1}{C_2} + dfrac{1}{C_3} \[4pt] &= dfrac{1}{1.000 mu F} + dfrac{1}{5.000 mu F} + dfrac{1}{8.000 mu F} \[4pt] &= dfrac{1.325}{mu F}.end{align*}$$
اکنون باید نتیجه را معکوس کنیم تا مقدار واقعی را داشته باشیم.
$$begin{align*} C_S &= dfrac{mu F}{1.325} \[4pt] &= 0.755 mu F.end{align*} nonumber$$
اثبات ظزفیت معادل اتصال موازی خازن
در اتصال موازی کاملا برعکس اتصال متوالی خازنها عمل میکنیم یعنی خازنها در اتصال موازی اختلاف پتانسیل یکسانی دارند ولی بار کل برابر جمع تمام بارهای خازنها خواهد بود.

$$Q = Q_1 + Q_2 + Q_3.$$
$$V_{P} = V_1 = V_2 = V_3.$$
با استفاده از رابطه $$C=dfrac{Q}{V}.$$ خواهیم داشت:
$$C_pV = C_1V + C_2V + C_3V.$$
بنابراین ظرفیت خازن معادل در مدار موازی به صورت زیر خواهد بود:
$$C_p = C_1 + C_2 + C_3.$$
مثال اول خازن موازی
ظرفیت معادل سه خازن $$1.000 mu F$$ و $$5.000 mu F$$ و $$8.000 mu F$$ را که به صورت موازی در مدار قرار دارند را محاسبه میکنیم.
پاسخ:
با استفاده از رابطه خازن معادل میتوانیم بهراحتی ظرفیت معادل این سه خازن را حساب کنیم.
$$begin{align*} C_p &= C_1 + C_2 + C_3 \[4pt] &= 1.0 mu F + 5.0 mu F + 8.0 mu F \[4pt] &= 14.0 mu F. end{align*}$$
نکته: در بسیاری از موارد اتصال خازنها به صورت ترکیبی از اتصال متوالی و موازی است. در این صورت، خازنهایی که با هم موازی هستند را با هم معادل میگیریم و سپس همین کار را با خازنهای متوالی میکنیم آنقدر این کار را تکرار میکنیم تا دیگر امکان معادل گرفتن خازن در مدار وجود نداشته باشد.
مثال اول خازن در مدار ترکیبی
با توجه به شکل زیر میخواهیم ظرفیت خازن معادل که سه خازن با ظرفیتهای $$C_1 = 12.0 mu F$$ و $$C_2 = 2.0 mu F$$ و $$C_3 = 4.0 mu F$$ در آن هستند و به اختلاف پتانسیل ۱۲ ولت وصل هستند و همچنین بار و ولتاژ هر خازن را حساب کنیم.
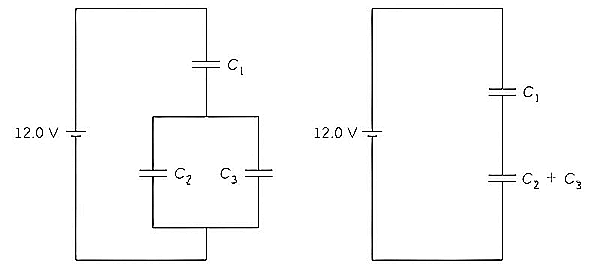
ابتدا باید خازن ۲ و۳ را که به صورت موازی در مدار قرار دارند معادل بگیریم و سپس حاصل را با خازن ۱ که به صورت متوالی است معادل میگیریم. از رابطه $$C=dfrac{Q}{V}$$ استفاده میکنیم تا بار و اختلاف پتانسیل برای هریک از خازنها را حساب کنیم.
$$C_{23} = C_2 + C_3 = 2.0 mu F + 4.0 mu F = 6.0 mu F.$$
$$dfrac{1}{C} = dfrac{1}{12.0 mu F} + dfrac{1}{6.0 mu F} = dfrac{1}{4.0 mu F} Rightarrow C = 4.0 mu F.$$
بنابراین ظرفیت خازن معادل کل برابر ۴ میکروفاراد است. اگر به قسمت (ب) شکل فوق دقت کنید، $$C_{1}$$ و $$C_{23}$$ با هم متوالی هستند بنابراین بار در آنها یکسان است ($$Q_1 = Q_{23}$$) همچنین ولتاژ بین آنها تقسیم میشود.
$$12.0 V = V_1 + V_{23} = dfrac{Q_1}{C_1} + dfrac{Q_{23}}{C_{23}} = dfrac{Q_1}{12.0 mu F} + dfrac{Q_1}{6.0 mu F} Rightarrow Q_1 = 48.0 mu C.$$
در نتیجه اختلاف پتانسیل در خازن ۱ برابر مقدار زیر است:
$$V_1 = dfrac{Q_1}{C_1} = dfrac{48.0 mu C}{12.0 mu F} = 4.0 V.$$
چون خازن ۲ و ۳ با هم موازی هستند در نتیجه اختلاف پتانسیل یکسانی دارند.
$$V_2 = V_3 = 12.0 V – 4.0 V = 8.0 V.$$
اکنون که اختلاف پتانسیل و ظرفیت خازنهای ۲ و۳ را داریم میتوانیم بارهای هریک را حساب کنیم.
$$Q_2 = C_2V_2 = (2.0 mu F)(8.0 V) = 16.0 mu C,$$
$$Q_3 = C_3V_3 = (4.0 mu F)(8.0 V) = 32.0 mu C.$$
همانطور که میدانیم چون خازنهای ۲ و ۳ موازی هستند بار معادل آنها برابر جمع جبری بار هر دو آنها است.
$$Q_{23} = Q_2 + Q_3 = 48.0 mu C.$$
انرژی ذخیره شده در خازن چیست؟
انرژی $$U_{c}$$ ذخیره شده در خازن از نوع پتانسیل الکترواستاتیک است که با بار الکتریکی $$Q$$ و ولتاژ $$V$$ بین صفحات خازن ارتباط دارد. یک خازن شارژ شده انرژی الکتریکی را بین صفحات خود ذخیره میکند. اگر منبع تغذیه را از خازن شارژ شده جدا کنیم، انرژی بین صفحات خازن باقی میماند.
برای درک بهتر این مفهوم یک خازن مسطح بدون دیالکتریک که بین صفحات آن خلا است را در نظر بگیرید، فضای بین صفحات خازن را Ad (حجم بین صفحات) و میدان الکترواستاتیکی بین آنها را ٍE فرض کنید. $$U_{c}$$ تمام انرژی خازن در بین فضای صفحات است. چگالی انرژی خازن برابر تقسیم $$U_{c}$$ بر Ad است. بنابراین اگر ما چگالی انرژی را بدانیم میتوانیم از رابطه $$U_C = u_E(Ad)$$ مقدار $$U_{c}$$ را حساب کنیم. همچنین رابطه چگالی انرژی خازن با میدان الکتریکی به صورت زیر است:
$$u_E = frac{1}{2} epsilon_0E^2.$$
همانطور که گفته شد اگر چگالی انرژی را در فضای بین صفحات ضرب کنیم، انرژی ذخیره شده در صفحات خازن مسطح را خواهیم داشت:
$$U_C = u_E(Ad) = frac{1}{2}epsilon_0E^2Ad = frac{1}{2}epsilon_0frac{V^2}{d^2}Ad = frac{1}{2}V^2epsilon_0 frac{A}{d} = frac{1}{2}V^2C$$
در اینجا فرض کردیم که میدان بین صفحات خازن یکنواخت است بنابراین میتوانیم از روابط زیر استفاده کنیم:
$$E=frac{V}{d}$$
$$C=frac{Q}{V}$$
$$C=frac{epsilon A}{d}$$
با جایگذاری آنها در نهایت انرژی خازن $$U_{c}$$ به صوزت زیر خواهد بود:
$$U_C = frac{1}{2}V^2C = frac{1}{2}frac{Q^2}{C} = frac{1}{2}QV. label{8.10}$$

امپدانس و راکتانس خازن چیست؟
امپدانس به زبان ساده، مقاومت اجزا مدار در برابر جریان است که با نماد Z نشان داده میشود و واحد اندازهگیری آن اهم است. در مدار با جریان مستقیم امپدانس و مقاومت یکی هستند و رابطه زیر برای آنها برقرار است:
$$R=frac{V}{I}$$
که در رابطه فوق:
- $$R$$ : مقاومت و واحد آن اهم
- $$V$$ : اختلاف پتانسیل و واحد آن ولت
- $$I$$ : جریان و واحد آن آمپر
در مدار با جریان متناوب به علت وجود بستگی عناصر خازن و القاگر به فرکانس کمیت دیگری به نام راکتانس داریم که با نماد X نشان داده میشود و واحد اندازهگیری آن نیز اهم است. امپدانس در مدار با جریان متناوب برابر جمع مقاومت و راکتانس است.
نتیجهگیری
خازن عنصری مهم و غیرقابل انکار در صنایع الکترونیک است که در همه جوانب صنعتی امروز بشر نقش دارد. در این قسمت از مجله فرادرس با مفهوم خازن چیست و نحوه عملکرد آن در مدار آشنا شدید همچنین اجزا مختلف خازن و انواع مختلف آن مورد بررسی قرار گرفت. همینطور مشخصات عمومی خازن و برخی از کاربردهای مهم معرفی شد. تکامل خازن و استفاده از آن به طور روزافزون ادامه دارد و در آینده شاهد پیشرفتهای بیشتری در حوزه الکترونیک خواهیم بود.
جدول کامل انواع دیالکتریک
| ماده | ثابت دیالکتریک ($$kappa$$) | قدرت دیالکتریک ($$V/m$$) |
| باکلیت | 4.9 | $$24 times 10^{6}$$ |
| کوارتز گداخته | 3.78 | $$8 times 10^{6}$$ |
| لاستیک نئوپرن | 6.7 | $$12 times 10^{6}$$ |
| نایلون | 3.4 | $$14 times 10^{6}$$ |
| کاغذ | 3.7 | $$16 times 10^{6}$$ |
| پلیاستایرن | 2.56 | $$24 times 10^{6}$$ |
| پیرکس | 5.6 | $$14 times 10^{6}$$ |
| روغن سیلیکون | 2.5 | $$15 times 10^{6}$$ |
|
تایتانات استرونتیوم |
233 | $$8 times 10^{6}$$ |
| آب | 80 | — |
فیلم های آموزش خازن چیست و چگونه کار می کند؟ – به زبان ساده + فیلم آموزشی رایگان
فیلم آموزشی خازن چیست؟
فیلم آموزشی محاسبه ظرفیت خازن مسطح
فیلم آموزشی محاسبه ظرفیت خازنهای استوانهای و کروی
فیلم آموزشی اتصالات خازنها و انرژی ذخیره شده در آنها
source