در حوزه یادگیری عمیق، «شبکه عصبی بازگشتی» (Recurrent Neural Networks |RNNs) برای پردازش دادههای متوالی، مانند دادههای سری زمانی، استفاده میشوند. دادههای سری زمانی دادههایی هستند که دارای نظمی مبتنی بر زمان هستند. برای مثال، جملاتی که در زبانهای مختلف به کار میگیریم نیز دارای ساختاری متوالی هستند. اصل کار شبکههای بازگشتی بر این اساس است که ورودیهای گذشته را با استفاده از یک حافظه داخلی در کاربردهایی نظیر پیشبینی قیمت سهام، تولید متن و ترجمه ماشینی، به خاطر میآورد. ما در این مطلب از مجله فرادرس یاد میگیریم که شبکه عصبی بازگشتی چیست و سپس معماری و ساختار این شبکه را تحلیل میکنیم. در ادامه، ۲ فرایند مهم انتشار رو به جلو و پسانتشار را با ذکر روابط و بررسی هر یک از آنها مورد بررسی قرار میدهیم. در انتها، یکی از معایب این شبکه را با عنوان مشکل «محو شدگی گرادیان» (Vanishing Gradient) را تحلیل میکنیم و به راهکارهای ارائه شده برای آن اشارهای خواهیم داشت.
شبکه عصبی بازگشتی چیست؟
«شبکه عصبی بازگشتی» (Recurrent Neural Networks |RNNs) یکی از انواع شبکههای عصبی است که برای پردازش دنبالههایی از دادهها با نمایش x(t) = x(1), …, x(τ) در زمانهای مشخص t، و با شروع از زمان ۱ تا τ، به کار میرود. این دسته از شبکهها بهتر است برای کاربردهایی نظیر «پردازش زبان طبیعی» (Natural Language Processing | NLP) و پردازش سیگنال مورد استفاده قرار بگیرند که دادهها را به صورت متوالی دریافت میکنند. برای مثال، در مسائل پردازش زبان طبیعی، هنگامی که میخواهید کلمه بعدی را در یک جمله پیشبینی کنید، دانستن کلمات قبلی آن در جمله، اهمیت بسیاری دارد. برای مثال جمله «I love dogs» را در نظر بگیرید، این جمله معنایی متفاوت با جمله «Dogs I love.» دارد. به زبان ساده، اگر معنای دادههای ما با تغییری در ترتیب آنها تغییر کند، ما دارای مجموعهدادهای ترتیبی هستیم و شبکههای RNN برای حل همین دسته از مسائل مورد استفاده قرار میگیرند.
علت اینکه این شبکه را بازگشتی مینامیم آن است که برای هر عنصر از دنباله به صورت بازگشتی وظیفه مشابهی را انجام میدهد. به این معنی که خروجی هر عنصر، به عنوان ورودی برای عنصر بعدی استفاده میشود. این امر باعث میشود که شبکه بتواند اطلاعات مربوط به عناصر قبلی را در حافظه خود ذخیره کند و از این اطلاعات برای پردازش عناصر بعدی استفاده کند. در ادامه فهرستی از کاربردهای متداول شبکههای عصبی بازگشتی را بیان میکنیم.
اگر با ساختار شبکههای عصبی آشنا باشید، به احتمال زیاد شبکه عصبی «پرسپترون چند لایه» (Multi Layer Perceptron| MLP) را به عنوان شبکهای با ساختار چند لایهای از نورونها را به یاد دارید. شبکههای بازگشتی در ۲ مورد زیر، با شبکههای پرسپترون چند لایه متفاوت هستند.
- شبکههای بازگشتی از اطلاعات گذشته استفاده میکنند.
- در شبکههای بازگشتی، پارامترها یا وزنها بین زمانها به اشتراک گذاشته میشوند. به این معنا که همان وزنها برای هر مرحله زمانی استفاده میشوند.
برای اینکه با طرز کار و مفهوم این شبکه کاملا آشنا بشویم، در ادامه، یادمیگیریم که معماری شبکه عصبی بازگشتی چیست و چگونه کار میکند.
معماری شبکه عصبی بازگشتی چیست؟
در این بخش به طور خلاصه معماری شبکه بازگشتی را مورد بررسی قرار میدهیم. به این منظور تصویر زیر را در نظر بگیرید.
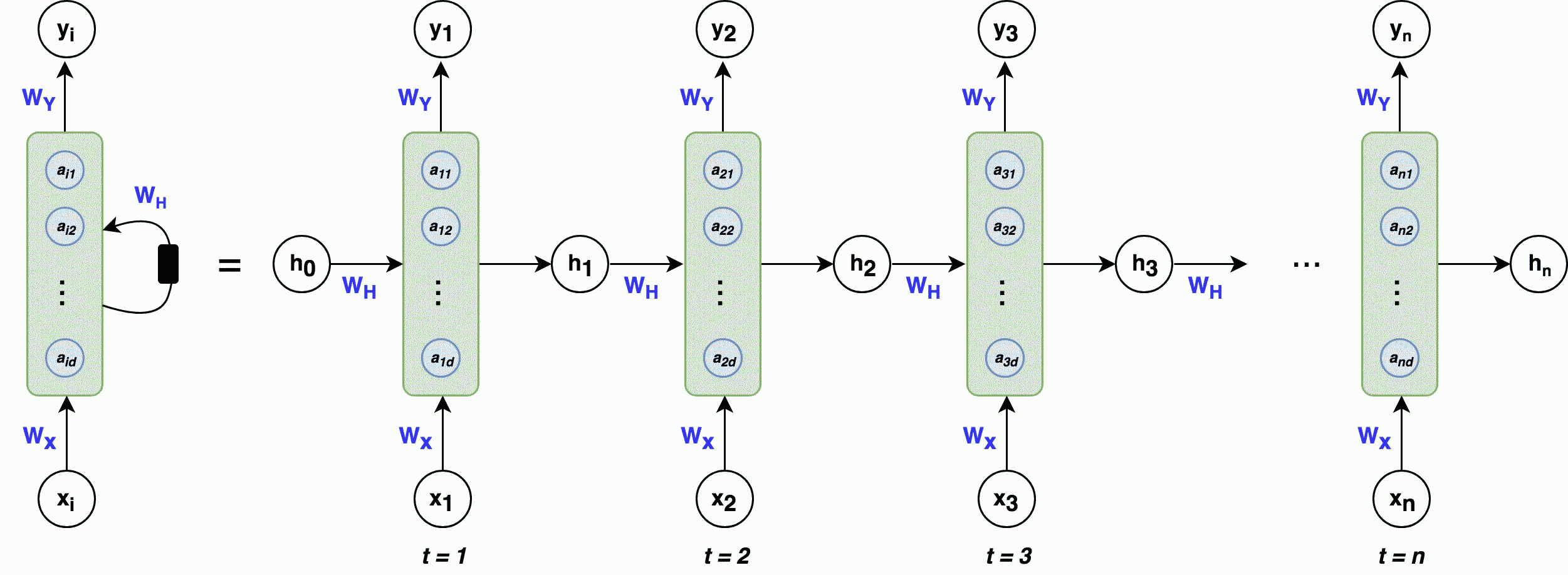
نگران نباشید اگر در حال حاضر تصویر بالا برای شما کمی گیجکننده است. در ادامه، این معماری را با تمام اجزا و به همراه مثال بررسی خواهیم کرد. این امر به شما کمک میکند تا نحوه عملکرد شبکه بازگشتی را به خوبی درک کنید. در این تصویر، قسمت چپ، شبکه عصبی بازگشتی یا RNN را بهطور کلی نشان میدهد. سمت راست تصویر، نیز همان شبکه را به صورت «باز شده» (Unfolded) نمایش میدهد. در این حالت، معماری شبکه به صورت دنبالهای از عناصر نمایش داده میشود که هر لایه مربوط به عنصری از دنباله است. این کار باعث میشود که بتوان عملکرد شبکه را برای هر عنصر از دنباله به طور جداگانه بررسی کرد. برای مثال، اگر دنباله ورودی مسئله، یک جمله ۳ کلمهای باشد شبکه باز شده – که در قسمت سمت راست تصویر بالا نمایش داده شده است، – شامل ۳ لایه میشود که هر کلمه مختص به یک لایه است. برای اینکه معماری شبکه بازگشتی را کامل درک کنیم، لازم است با موارد زیر که در تصویر به چشم میخورد، آشنا شویم.
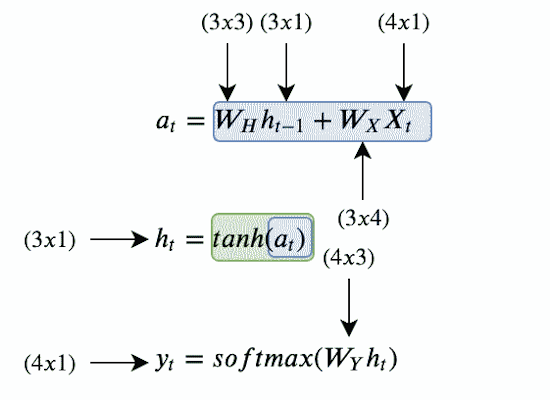
در تصویری که آوردهایم، بلوکهای سبزرنگ حالت نهان نامیده میشوند. دایرههای آبیرنگ که با نماد a در هر بلوک تعریف شدهاند، به عنوان گرههای نهان یا واحدهای نهان شناخته میشوند که تعداد این گرهها با استفاده از پارامتر d تعیین میشود. بنابراین، d برابر با طول بردار $$h_{t}$$ است. بهطور کلی، در این معماری هر گام زمانی دارای یک ورودی $$x_{t}$$، یک حالت پنهان $$h_{t}$$ و یک خروجی $$y_{t}$$ است و وزنهای مربوط به ورودیها، حالتهای پنهان و خروجیها به ترتیب با $$W_{H}$$ ،$$W_{X}$$ و $$W_{Y}$$ نشان داده میشوند. حال نیاز است با برخی مفاهیم دیگر در این تصویر آشنا شویم.
ورودی
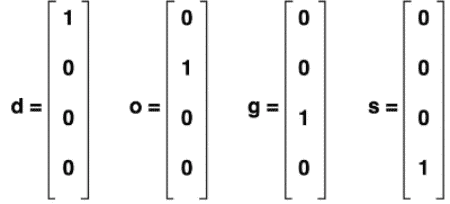
در این بخش، میخواهیم بدانیم که ورودی در شبکه عصبی بازگشتی چیست. ورودی، دنبالهای از نقاط داده است که در آن هر نقطه داده به موقعیت یا زمانی خاص در دنباله مربوط میشود. شبکه RNN در هر زمان یک بردار ورودی $$x_{t}$$ به حالت نهان دریافت میکند. برای مثال اگر کاراکترهای کلمه «dogs» را به عنوان ورودی شبکه بازگشتی در نظر داشته باشیم، هر یک از این کاراکترها به صورت زیر میتواند به عنوان ورودی به شبکه بازگشتی وارد شود. در مثال زیر هر کاراکتر در کلمه “dogs” به برداری با ابعاد ۱×۴ رمزگذاری شده است. و در قالب یک بردار «One-hot» به عنوان ورودی به شبکه داده میشود.
حالت نهان
حالت نهان، حافظه شبکه بازگشتی محسوب میشود. این حافظه، اطلاعات مربوط به ورودیهای قبلی شبکه را ذخیره میکند. حالت نهان در زمان t، معمولا با نماد $$h_{t}$$ نشان داده میشود. $$h_{t}$$ برداری است که بر اساس ورودی فعلی و حالت نهان مرحله زمانی قبلی محاسبه میشود. توجه داشته باشید که بردار $$h_{0}$$ معمولا صفر در نظر میگیرند، زیرا الگوریتم هیچ اطلاعات قبلی از اولین عنصر دنباله ندارد. فرمول محاسبه $$h_{t}$$ به صورت زیر است.
$$h_{t} = f(W_{x}x_{t} + W_{h}h_{t-1}) $$
تابع f یک تبدیل غیر خطی مانند tanh یا ReLU است که به شبکه کمک میکند تا الگوهای پیچیدهتر و غیرخطی را در دادهها شناسایی کند. همچنین، $$W_{x}$$ و $$W_{y}$$ ماتریس وزن و یا به عبارتی پارامترهای شبکه هستند که وظیفه دارند وزنهای مرتبط با ورودیها و حالتهای نهان را تعیین کنند که در بخش بعدی این پارامترها را بیشتر توضیح میدهیم.
خروجی
خروجی شبکه RNN پیشبینی مورد نظر را بر اساس دادههای ترتیبی تولید میکند. خروجی میتواند بسته به وظیفه مورد نظر، متفاوت باشد. به عنوان مثال، در مدلسازی زبان، بردار خروجی میتواند کلمه بعدی در یک جمله را پیشبینی کند. تحلیل احساسات میتواند با پیشبینی احساس یک متن داده شده، اطلاعات سودمندی را در مورد آن متن ارائه دهد. بهطور کلی، در شبکه عصبی بازگشتی، هر گام زمانی شامل یک خروجی $$y_{t}$$ است که میتواند به عنوان خروجی نهایی شبکه در گام زمانی t در نظر گرفته شود.
وزن ها
در فرایند یادگیری، شبکههای بازگشتی به طور مداوم وزنهای خود را به گونهای تنظیم میکنند که خطا را کاهش دهند. این وزن ها شامل موارد زیر است.
- $$W_{X}$$: ماتریس وزن برای بردار ورودی $$x_{t}$$ به حالت نهان $$h_{t}$$ در گام زمانی t
- $$W_{H}$$: ماتریس وزن برای حالت نهان $$h_{t-1}$$ به حالت نهان $$h_{t}$$ در گام زمانی t
- $$W_{Y}$$: ماتریس وزن از حالت نهان $$h_{t}$$ به خروجی در گام زمانی t
ماتریسهای وزن $$W_{H}$$ ،$$W_{X}$$ و $$W_{Y}$$ در فرایند یادگیری شبکه توسط الگوریتم بهینهسازی بهروزرسانی میشوند تا مدل بهترین وزنها را به منظور پیشبینی درست یاد بگیرد. این وزنها در تمام گامهای زمانی، یکسان هستند، یا عبارتی دیگر، به اشتراک گذاشته میشوند. به مثال زیر توجه کنید.
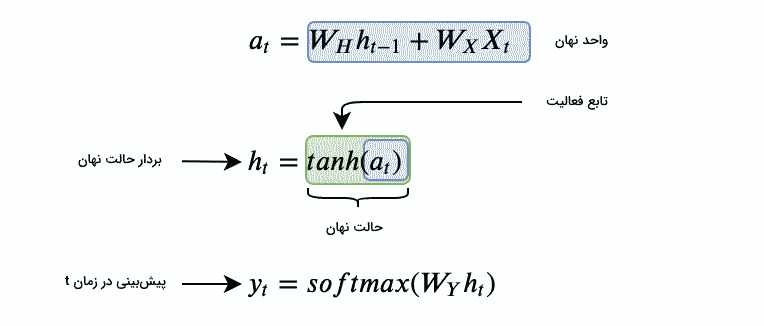
در این مثال، واحد نهان در گام زمانی t، با ترکیب ورودی x در زمان t و حالت نهان در گام زمانی قبل، همچنین اعمال ماتریس وزن بر روی هر یک از آنها، محاسبه میشود. حال، برای به دست آوردن بردار $$h_{t}$$ که بردار حالت نهان در زمان t است، تابع فعالسازی «تانژانت هیپربولیک» (tanh) به واحد نهان اِعمال میشود که توسط بلوک سبزرنگ نشان داده شده است. اکنون، کافی است برای به دست آوردن خروجی حالت کنونی، ماتریس وزن خروجی به بردار حالت نهان اِعمال شود که به منظور پیشبینی، تابع فعالسازی «Softmax» نیز وارد شده است. در این بخش، مثال سادهای را در نظر میگیریم و سپس، بردار نهان و خروجی را برای این مسئله خاص، محاسبه میکنیم. برای پیشبینی حرف «s» پس از ورود کاراکترهای «o»، «d»، و «g»، میتوان از شبکه RNN با معماری زیر استفاده کرد.
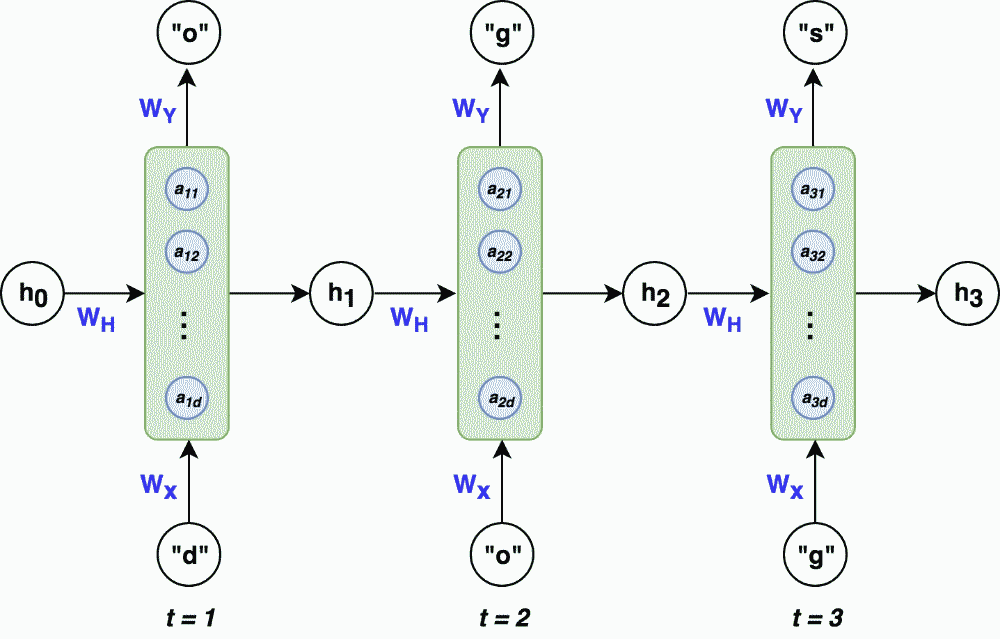
در ادامه میخواهیم فرایند انتشار رو به جلو را برای این شبکه با استفاده از مثالی ساده یاد بگیریم. احتمالاً بدانید که عملیات انتشار رو به جلو، در شبکه عصبی، فرایند انتقال اطلاعات از لایه ورودی به لایههای عمیقتر به منظور ایجاد خروجی است. این فرایند شامل محاسبه و انتقال ویژگیها به صورت تدریجی از لایه ابتدایی به لایههای بعدی است که در نهایت به تولید خروجی مناسب منجر میشود. در این مثال، فرض میکنیم بردار حالت نهان $$h_{t}$$ به طول ۳ و بردار ورودی $$x_{t}$$ – یا به عبارتی دیگر، بردار وان هات برای هر کاراکتر، – طولی برابر با ۴ داشته باشد.
انتشار رو به جلو
در گام زمانی t=۱، فرایند انتشار رو به جلو به صورت زیر انجام میشود.
- محاسبه واحد نهان a
- اعمال «تابع فعالسازی» (Activation Function) به واحد نهان و به دست آوردن بردار نهان $$h_{t}$$
- محاسبه مقدار خروجی یا همان پیشبینی مسئله
برای گام زمانی t=۱، عملیات زیر را انجام میدهیم. برای ملموستر شدن مسئله، ماتریسهای وزن $$W_{H}$$ ،$$W_{X}$$ و $$W_{Y}$$ را به صورت «تصادفی» (Random) – همانند آنچه در پیادهسازی شبکه اتفاق میافتد- مقداردهی اولیه میکنیم. اکنون، به محاسبات زیر توجه کنید.
$$a_{1} $$ = begin{pmatrix} 0.1 & 0.5 & 0.1 \ 0.5 & 0.9 & 0.3 \ 0.3 & 0.2 & 0.1 end{pmatrix} begin{pmatrix} 0 \ 0 \ 0 end{pmatrix} + begin{pmatrix}
0.6 & 0.8 & 0.4 & 0.8 \ 0.2 & 0.2 & 0.8 & 0.7 \ 0.9 & 0.8 & 0.1 & 0.2 end{pmatrix} begin{pmatrix}1 \ 0 \ 0 \ 0 end{pmatrix} = begin{pmatrix} 0.6 \ 0.2 \ 0.9 end{pmatrix}
$$h_{1} $$= $$ tanh $$ (begin{pmatrix} 0.6 \ 0.2 \0.9 end{pmatrix}) = begin{pmatrix} 0.54 \ 0.20 \ 0.72 end{pmatrix}
در گام زمانی ۱، بردار نهان $$h_{t}$$ به صورت پیشفرض صفر است. با استفاده از روابطی که برای محاسبه بردار نهان و خروجی ارائه داده بودیم، بردار خروجی را برای کاراکتر بعد از «d» محاسبه کردیم. خروجی پیشبینی شده کاراکتر «d» است که صحیح نیست. اما، این پیشبینی غلط، قابل انتظار است، زیرا وزنها به صورت تصادفی انتخاب شدهاند و هنوز آموزش ندیدهاند. هدف این بخش تنها آشنایی با نحوه محاسبه بردار نهان و خروجی در فرایند انتشار رو به جلو است. به همین ترتیب، در گام زمانی ۲ و ۳، نحوه محاسبات، مشابه گام زمانی ۱ است، با این تفاوت که بردار $$h_{t-1}$$ دیگر صفر نیست، بلکه مقدار بردار نهان گام زمانی قبلی است.

همچنین، توجه داشته باشید که شبکههای RNN در هر مرحله زمانی یک پیشبینی تولید میکنند. اما، بسته به نوع مسئله، ممکن است تنها به پیشبینی گام زمانی آخر نیاز داشته باشید. به عنوان مثال، در همین مسئله که هدف پیشبینی کاراکتر بعد از کلمه «dog» است. میتوانیم تنها خروجی گام زمانی ۳ را در نظر داشته باشیم و بقیه را نادیده بگیریم.
تا اینجا یاد گرفتیم که شبکه عصبی بازگشتی چیست و چگونه پیشبینی میکند یا به عبارتی دیگر، نحوه محاسبات در فرایند انتشار رو به جلو در شبکه بازگشتی را یاد گرفتیم. حال، میخواهیم بدانیم که شبکه بازگشتی چگونه آموزش میبیند و یا پیشبینیهای درست را یاد میگیرد. اگر با مفاهیم شبکههای عصبی آشنا باشید، احتمالا، میدانید که این امر نیازمند فرایند «پسانتشار» (Backpropagation) است. یادآوری میکنیم که فرایند پسانتشار یک مرحله مهم در آموزش شبکههای عصبی است که شامل محاسبه خطا، انتقال خطا به عقب و و بهروزرسانی وزنها بر اساس مشتقات جزئی نسبت به همان وزنها است.
فرایند پس انتشار
درک چگونگی فرایند پسانتشار در شبکههای بازگشتی به دلیل ماهیت بازگشتی شبکه ممکن است کمی سختتر به نظر برسد. ما در این بخش کاملاً این فرایند را شرح میدهیم تا فهم آن را برای شما آسانتر کنیم. در شبکه بازگشتی فرایند پسانتشار شامل مراحل زیر است.
- ماتریسهای وزن $$W_{H}$$ ،$$W_{X}$$ و $$W_{Y}$$ بهصورت تصادفی مقداردهی اولیه میشوند.
- عملیات انتشار روبهجلو به منظور محاسبه پیشبینیها انجام میشود.
- میزان خطا محاسبه میشود. این خطا نشان میدهد که خروجی شبکه تا چه حد با خروجی مورد انتظار مطابقت دارد. به عبارتی دیگر در این مرحله، خطا محاسبه میشود تا مشخص شود شبکه تا چه اندازه عملکرد خوبی داشته است.
- گرادیانها با استفاده از پسانتشار خطا محاسبه میشوند و نمایانگر نرخ تغییر خطا نسبت به تغییر وزنهای شبکه است. این گرادیانها به عنوان راهنمایی برای تعیین جهت بهینهسازی وزنهای شبکه عمل میکنند.
- در این مرحله وزنها با استفاده از مقادیر گرادیان محاسبه شده بهروزرسانی میشوند تا میزان خطا کاهش یابد. این بهروزرسانیها به شبکه کمک میکنند تا یاد بگیرد و عملکرد خود را بهبود بخشد.
مراحل ۲ تا ۵ تا زمانی که شبکه به عملکرد مطلوبی برسد تکرار میشود. به این ترتیب، عملیات پسانتشار به شبکه اجازه میدهد تا از خطاهایش بیاموزد و به طور مداوم عملکرد خود را بهبود بخشد.

برای آشنایی بیشتر با نحوه عملکرد شبکه RNN همان مثال قبلی را که در بخش فرایند انتشار رو به جلو در نظر داشتیم را اینبار در فرایند پس انشار مورد بررسی قرار میدهیم. مثال پیش بینی کاراکتر بعدی، برای کلمه «dogs» را میتوان به صورت یک مسئله طبقهبندی در نظر گرفت. از این رو میتوان تابع هزینه «Multi-Class Cross Entropy» برای محاسبه خطا در این مسئله مناسب دانست. در ادامه رابطه این تابع هزینه را آوردهایم.
$$L_t(y_t, hat{y}_t) = -y_t log(hat{y}_t) $$
همانطور که گفتیم در شبکه بازگشتی اطلاعات از یک گام زمانی به گام زمانی بعدی منتقل میشوند و هر گام زمانی معادل یک مرحله در فرایند پیشبینی است. بنابراین برای محاسبه خطا یا «تابع هزینه» (Loss Function)، از تمام گامهای زمانی مختلف در یک «دنباله» (sequence) استفاده میکنیم. به عبارت دیگر، خطا به ازای هر گام زمانی محاسبه میشود و سپس خطاهای تمام گامها با یکدیگر جمع و به عنوان «خطای کلی» (overall loss) در نظر گرفته میشود. اهمیت این کار در این است که شبکه باید از خطاهای تمام گامهای زمانی یاد بگیرد تا عملکرد بهتری در تمام طول دنباله داشته باشد. به این ترتیب، توانایی پیشبینی بهتر در تمام دنباله تقویت میشود. تابع هزینه کلی را میتوان با استفاده از رابطه زیر بیان کرد.
$$L_{text{total}}(y, hat{y}) = – sum_{t=1}^{n} y_t log(hat{y_t})$$
در ادامه، تصویری آورده شده است که این مفاهیم را به درستی نشان میدهد.
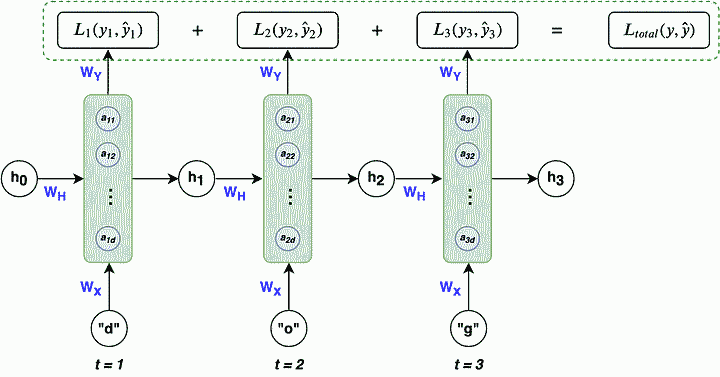
در این مرحله، لازم است گرادیانهای ۳ ماتریس وزن $$W_{H}$$ ،$$W_{X}$$ و $$W_{Y}$$ را نسبت به تابع هزینه محاسبه کنیم. سپس، با استفاده از نرخ یادگیری η، آنها را بهروزرسانی میکنیم. وزنها با استفاده از رابطه زیر بهروزرسانی میشوند تا هزینه را به حداقل برسانند. به بیانی دیگر, در این مرحله نیاز است از یک الگوریتم بهینهسازی برای آموزش مدل یا همان به روزرسانی وزنها استفاده کنیم. رابطهای که در ادامه آوردهایم مربوط به الگوریتم بهینه ساری «گرادیان کاهشی» (Gradient descent) است. در این رابطه، i میتواند x، y یا h باشد و ما از اندیس i برای نمایندگی از هر یک از وزنها استفاده کردهایم.
$$W_i := W_i – eta frac{partial L_{text{total}}(y, hat{y})}{partial W_i}$$
در این بخش، نحوه محاسبه گرادیان وزنها را شرح میدهیم که یک مرحله مهم در فرایند آموزش شبکه عصبی محسوب میشود. همانطور که قبلاً اشاره کردیم، در شبکههای بازگشتی، وزنها در تمامی گامهای زمانی بر هزینه کلی تأثیرگذار هستند. برای این منظور، محاسبه گرادیان وزنها با توجه به گامهای مختلف زمانی انجام میشود.

برای فهم بهتر این مسئله، به تفصیل به محاسبه گرادیانها برای وزنهای $$W_{X}$$ و $$W_{Y}$$ میپردازیم. از آنجا که نحوه محاسبه گرادیان برای $$W_{H}$$ مشابهت زیادی با $$W_{X}$$ دارد، محاسبه آن را به عهده خودتان میگذاریم. اکنون، به محاسبه گرادیان برای وزن $$W_{Y}$$ میپردازیم که محاسبات سادهتری دارد. برای بهینهسازی وزن $$W_{Y}$$، لازم است گرادیان تابع هزینه نسبت به $$W_{Y}$$ محاسبه شود. در رابطهای که در ادامه آوردهایم رابطه بین تابع هزینه و وزن $$W_{Y}$$ در شبکه بازگشتی نشان داده شده است.
$$L_t = -y_t log(hat{y_t}) rightarrow hat{y_t} = text{softmax}(z_t) rightarrow z_t = W_Yh_t$$
با توجه به رابطه بالا، حال، به منظور محاسبه گرادیان تابع هزینه نسبت به وزن $$W_{Y}$$ کافی است از «قاعده زنجیرهای» (Chain Rule) پیروی کنیم. احتمالا به یاد دارید که قاعده زنجیرهای یک قاعده مهم در حسابان است که برای محاسبه مشتقات توابع مرکب استفاده میشود. رابطه زیر نحوه محاسبه گرادیان برای تابع هزینه را نمایش میدهد.
$$frac{partial L_t}{partial W_Y} = frac{partial L_t}{partial hat{y_t}} cdot frac{partial hat{y_t}}{partial z_t} cdot frac{partial z_t}{partial W_Y}$$
همانطور که قبلاً گفته شد، در شبکههای بازگشتی، تابع هزینه مجموعی از هزینههای گامهای زمانی مختلف در مسئله مورد نظر ما است. بنابراین، برای به دست آوردن گرادیانها، لازم است همان قواعد گفته شده در روابط ارائه شده در بالا را در تابع هزینه کلی اجرا کنیم که به رابطه زیر میرسیم.
$$frac{partial L_{text{total}}}{partial W_Y} = frac{partial L_1}{partial hat{y_1}} frac{partial hat{y_1}}{partial z_1} frac{partial z_1}{partial W_Y} + frac{partial L_2}{partial hat{y_2}} frac{partial hat{y_2}}{partial z_2} frac{partial z_2}{partial W_Y} + frac{partial L_3}{partial hat{y_3}} frac{partial hat{y_3}}{partial z_3} frac{partial z_3}{partial W_Y}
= sum_{t=1}^{n} frac{partial L_t}{partial W_Y} $$
در این قسمت نگاهی به محاسبه گرادیان برای وزن $$W_{X}$$ خواهیم داشت که نسبت به محاسبات قبلی کمی دشوارتر است. زیرا برای محاسبه گرادیان وزن $$W_{X}$$ نیاز است با استفاده از قاعده زنجیرهای روابط بازگشتی را تا گام زمانی t=0 پیش برویم. برای اینکه مطلب برایتان روشنتر شود به روابط زیر توجه کنید.
برای محاسبه گرادیان وزن $$W_{X}$$، ابتدا لازم است رابطه بین تابع هزینه و وزن $$W_{X}$$ را به دست آوریم که این روابط به صورت زیر قابل مشاهده است.
$$ L_t = -y_t log(hat{y}_t) rightarrow hat{y}_t = text{softmax}(z_t) rightarrow z_t = W_{Y} h_t rightarrow h_t = tanh(W_{H} h_{t-1} + W_X X_t) $$
حال با توجه به این که در قسمت قبل رابطه بین تابع هزینه و وزن $$W_{X}$$ را به دست آوردیم، با استفاده از رابطه زیر میتوان گردیان تابع هزینه نسبت به متغیر $$W_{X}$$ را محاسبه کرد.
$$frac{partial L_t}{partial W_X} = frac{partial L_t}{partial hat{y}_t} cdot frac{partial hat{y}_t}{partial z_{t}} cdot frac{partial z_{1}}{partial h_{1}} cdot frac{partial h_{1}}{partial W_x}$$
به این نکته توجه داشته باشید که دسترسی به متغیر $$W_{X}$$ در داخل رابطه $$h_{t}$$ امکان پذیر است و با توجه به آنکه تابع $$h_{t}$$ بازگشتی است، به همین ترتیب متغیر$$W_{X}$$ در $$h_{t-1}$$ نیز یافت میشود. پس با استفاده از قاعده زنجیرهای در روابط بازگشتی نیاز است تا $$h_{0}$$ محاسبه گرادیان را برای وزن $$W_{X}$$ پیش برویم. روابط زیر این موضوع را به خوبی نشان میدهد.
$$ frac{partial L_t}{partial W_X} = frac{partial L_t}{partial hat{y}_t} frac{partial hat{y}_t}{partial z_t} frac{partial z_t}{partial h_t} frac{partial h_t}{partial W_x} +frac{partial L_t}{partial hat{y}_t} frac{partial hat{y}_t}{partial z_t} frac{partial z_t}{partial h_t} frac{partial h_t}{partial h_{t-1}}frac{partial h_{t-1}}{partial W_{X}} ldots + frac{partial L_t}{partial hat{y}_t} frac{partial hat{y}_t}{partial z_t} frac{partial z_t}{partial h_t} frac{partial h_t}{partial h_{t-n}}frac{partial h_{t-n}}{partial W_{X}}
= sum_{k=0}^{N}frac{partial L_t}{partial hat{y}_t} frac{partial hat{y}_t}{partial z_t} frac{partial z_t}{partial h_t}frac{partial h_t}{partial h_k} frac{partial h_k}{partial W_x} $$
گرادیان تابع هزینه کلی – که مجموع توابع هزینه در گام زمانی مختلف است،- به نسبت وزن $$W_{X}$$ در رابطه زیر قابل مشاهده است.
$$frac{partial L_{text{total}}}{partial W_X} = sum_{t=1}^{n} sum_{k=0}^{n} frac{partial L_1}{partial y_j} frac{partial hat{y_t}}{partial z_t} frac{partial z_t}{partial h_t} frac{partial h_k}{partial W_x}$$
به همین ترتیب گرادیان را برای وزن $$W_{H}$$ میتوان محاسبه کرد. حال که گرادیانهای $$W_{H}$$ ،$$W_{X}$$ و $$W_{Y}$$ را به دست آوردیم، با استفاده از رابطه بهروزرسانی وزنها، این وزنها را بهروز میکنیم تا شبکه بتواند از تجربیات خود یاد بگیرد و عملکرد خود را بهبود بخشد. این عملیات که پسانتشار نامیده میشود را بارها تکرار میکنیم تا شبکه RNN به دقت مورد نظر دست یابد. اکنون که یاد گرفتیم شبکه بازگشتی چگونه آموزش میبیند و پیشبینی میکند، بیاییم به یکی از معایب مهم شبکههای بازگشتی اشاره کنیم و این مطلب از مجله فرادرس را به پایان برسانیم.
مشکل محو شدگی گرادیان در شبکه عصبی بازگشتی چیست؟
تا اینجا یاد گرفتیم که شبکه عصبی بازگشتی چیست و چگونه عمل میکند حال، در این بخش به یکی از معایب این شبکه میپردازیم و علت آن را بررسی میکنیم. یکی از مشکلاتی که شبکههای عصبی بازگشتی یا RNN با آن مواجه هستند، مشکل محو شدگی گرادیان است که بهطور کلی، هنگام آموزش شبکههای عصبی با روشهای مبتنی بر گرادیان مانند روش «پسانتشار» (Back Propagation) رخ میدهد. این مشکل باعث میشود که وزنهای لایههای ابتدایی شبکه به درستی به روزرسانی نشوند. به عبارتی دیگر، زمانی که شبکه عصبی قادر به انتشار اطلاعات مفید گرادیان از لایههای انتهایی به لایههای ابتدایی مدل نباشد مشکل محو شدگی گرادیان به وجود میآید که این امر در شبکههایی با تعداد لایههای زیادتر بیشتر بروز میکند.
زمانی که شبکه عصبی بازگشتی قصد انتقال اطلاعات از گامهای زمانی انتهایی به گامهای زمانی ابتدایی را دارد، اهمیت گرادیانهای مربوط به گامهای زمانی ابتدایی به مرور زمان کاهش مییابد. این افت اهمیت، موجب میشود که اطلاعات حاصل از ورودیهای ابتدایی تا حدودی از دست میرود. در شبکههایی با تعداد لایههای بیشتر – که در شبکههای بازگشتی با طولانی شدن دنباله ورودی این اتفاق میافتد – ، این مشکل به شدت جدیتر میشود زیرا هر لایه اضافی میتواند تأثیر بیشتری بر روی از دست دادن اطلاعات گرادیان مربوط به لایههای اولیه شوند. به عنوان مثال، در نظر بگیرید که جملهای مانند زیر به شبکه RNN داده میشود.

فرض کنید در این مثال قرار است که ۲ کلمه آخر یعنی «german» و «shepherd» پیشبینی بشود، RNN باید به ورودیهای «brown ،«black» و «dog» که اسمها و صفتهای توصیف کننده یک سگ شِپِرد آلمانی هستند، توجه کند. اما همانطور که ملاحظه میکنید کلمه «brown» از کلمه «shepherd» فاصله زیادی دارد. پیشتر با نحوه محاسبه گرادیان نسبت به $$W_{X}$$ در شبکه RNN آشنا شدیم. اکنون، با استفاده از مفاهیم گفته شده در بالا، میتوانیم خطای پسانتشار کلمه «shepherd» را به کلمه «brown» با استفاده از رابطه زیر محاسبه کنیم. نحوه محاسبه گرادیان نسبت به $$W_{X}$$ برای این مثال، به صورت زیر به دست میآید.
$$frac{partial L_{15}}{partial hat{y}_{15}}frac{partial hat{y}_{15}}{partial z_{15}}frac{partial z_{15}}{partial h_{15}}frac{partial h_{15}}{partial h_{2}}frac{partial h_{2}}{partial W_{x}}$$
از آنجا که تابع $$h_{t}$$ در گام زمانی ابتدایی تا به آخر به صورت بازگشتی تکرار شده است، با استفاده از قانون زنجیرهای، قسمتی از رابطه بالا به صورت زیر بازنویسی میشود. رابطه زیر نشان میدهد که محاسبه خطای پسانتشار مربوط به کلمه ابتدایی جمله از حاصل ضرب زنجیرهای نسبتا طولانی از مشتقهای جزئی به دست میآید.
$$frac{partial h_{15}}{partial h_{2}}=frac{partial h_{15}}{partial h_{14}}frac{partial h_{14}}{partial h_{13}}…frac{partial h_{2}}{partial h_{1}}$$
وجود زنجیرههای طولانی گرادیان میتواند مشکلساز باشد زیرا اگر کمتر از مقدار ۱ باشند، میتوانند باعث شوند خطای پسانتشار مربوط به کلمه «brown» تقریباً به صفر نزدیک شود. این امر به این معناست که کلمه «brown» هنگام عملیات انتشار رو به جلو، تأثیری اندک یا حتی صفر بر پیشبینی کلمه «shepherd» دارد. این مسئله یکی از معایب بزرگ شبکههای باز گشتی یا همان RNNها است. مشکل محوشدگی گرادیان در شبکههای بازگشتی را میتوان اینگونه تفسیر کرد که شبکههای RNN در پردازش جملات طولانی یا دادههای ورودی متوالی با طول زیاد عملکرد خوبی ندارند.
به عبارت دیگر، این شبکهها از حافظه کافی برخوردار نیستند. به همین دلیل، شبکههای جدیدی مانند «واحد بازگشتی گیتی» (Gated Recurrent Unit | GRU) و «حافظه طولانی کوتاه مدت» ( Long Short-Term Memory | LSTM) معرفی شدند که توانستند تا حدی مشکل محوشدگی گرادیان را حل کنند. این شبکهها از حافظه بهتری برخوردار هستند. در این مجله از فرادرس به این شبکهها پرداخته نمیشود و در مقالات دیگری این مسئله را بررسی میکنیم.
سؤالات متداول
تا این قسمت از مطلب یاد گرفتیم که شبکه عصبی بازگشتی چیست و چگونه کار میکند. سپس، به یکی معایب مهم این شبکه با ذکر مثال پرداختیم. در ادامه، به سؤالات متداول پیرامون «شبکه عصبی بازگشتی» (RNN) میپردازیم.
مشکل اصلی شبکه عصبی بازگشتی چیست؟
شبکههای عصبی بازگشتی یا RNN برای مدلسازی دادههای ترتیبی و مبتنی بر زمان مانند پیش بینی بازار سهام، ترجمه ماشینی و تولید متن بسیار مفید هستند. با این حال، آموزش شبکه های عصبی بازگشتی به دلیل مشکل محو شدگی گرادیان دشوار است. مشکل محو شدگی گرادیان هنگامی رخ میدهد که گرادیان تابع هزینه با توجه به پارامترهای شبکه عصبی بازگشتی در طول زمان بسیار کوچک میشود. این امر باعث میشود که شبکه عصبی بازگشتی نتواند «وابستگی های طولانی مدت» (Long Term Dependency) را در دادهها بیاموزد، که این امر، برای وظایفی مانند ترجمه ماشینی و تولید متن بسیار مهم است.
چه تابع بهینه سازی برای شبکه بازگشتی RNN مناسب است؟
«RMSprop»، مخفف عبارت «Root Mean Square Propagation» یکی از الگوریتمهای بهینهسازی محبوب برای آموزش شبکههای عصبی به ویژه شبکههای عصبی بازگشتی یا همان RNN به شمار میآید. این الگوریتم برای RNNها به دلیل توانایی در مدیریت مشکلاتی نظیر محو شدگی گرادیان توصیه میشود که اغلب در فرایند یادگیری شبکههای بازگشتی رخ میدهد.
جمع بندی
ما در این مطلب از مجله فرادرس یاد گرفتیم که شبکه عصبی بازگشتی چیست و معماری شبکه بازگشتی را مورد بررسی قرار دادیم. در این ساختار، روابط بین اجزای مختلف شبکه به دقت مورد بررسی قرار گرفتهاند. این شبکهها برای مدلسازی دادههای دنبالهای، مانند زبان طبیعی یا سیگنالهای زمانی، به کار میروند. ما روابط و ارتباطات بین واحدهای زمانی مختلف در شبکه را نیز بهصورت دقیق تشریح کردیم.
هرچند که معماری شبکه بازگشتی قابلیت مدلسازی دنبالهها را دارا است، اما در پردازش دنبالههای طولانی ایرادی بر آنها وارد است که مرتبط با مسئله محو شدگی گرادیان است. این مشکل زمانی رخ میدهد که دنبالهای طولانی از دادههای متوالی به شبکه بازگشتی داده میشود. در این صورت، شبکه قادر به یادگیری و انتقال اطلاعات در گامهای زمانی ابتدایی شبکه نیست. برای توضیح این مشکل، مثالی ذکر شده است که نشان میدهد در یک جمله طولانی، شبکه قادر به پیشبینی بر اساس کلمات اولیه جمله نمیباشد. همچنین، در ادامه این مطلب به برخی از سؤالات متداول پیرامون شبکههای عصبی بازگشتی پرداختیم.
source