آرک تانژانت، تانژانت معکوس یا تانژانت وارون، یک تابع معکوس مثلثاتی است که عکس تابع تانژانت عمل میکند. روشهای مختلفی برای محاسبه این تابع وجود دارد. سادهترین و سریعترین روش برای محاسبه آرک تانژانت، استفاده از ماشینحساب مهندسی است. در این مطلب از مجله فرادرس، ابتدا به سوال ارک تانژانت چیست پاسخ میدهیم. سپس، ضمن آموزش روشهای محاسبه، فرمول مشتق، فرمول انتگرال و اتحادهای این تابع معکوس مثلثاتی را معرفی میکنیم.
ارک تانژانت چیست؟
«آرکتانژانت» (Arctangent)، یکی از انواع توابع معکوس مثلثاتی است که وارون تابع تانژانت را نمایش میدهد. ارک تانژانت با عبارتهای دیگری نظیر «تانژانت معکوس یا تانژانت وارون» (Inverse Tangent) نیز شناخته میشود.
این تابع معکوس مثلثاتی، معمولا به یکی از فرمهای زیر در عبارتهای جبری مورد استفاده قرار میگیرد:
$$ arctan $$
$$ tan ^ { – ۱ } $$

مفهوم ارک تانژانت چیست؟
تابعی مانند تابع زیر را در نظر بگیرید:
$$ y = f ( x ) $$
با جایگذاری متغیر ورودی $$ x $$ در این تابع، به متغیر خروجی $$ y $$ میرسیم. اکنون اگر تابعی مانند $$ g ( y ) $$ را داشته باشیم که با گرفتن متغیر $$ y $$ به عنوان ورودی، خروجی آن برابر با $$ x $ شود،
$$ g ( y ) = x $$
میگوییم تابع $$ g ( y ) $$، تابع معکوس یا تابع وارون $$ f ( x ) $$ است. این تابع معکوس را میتوانیم به صورت $$ f ^ { – ۱ } ( x ) $$ نمایش دهیم. مفهوم تابع ارک تانژانت نیز همین گونه است. تابع تانژانت، با گرفتن یک درجه (بر حسب زاویه، رادیان و غیره)، یک مقدار عددی را به ما میدهد. به عنوان مثال، تانژانت زاویه ۴۵ درجه برابر با ۱ میشود:
$$ tan ۴۵ ^ { circ } = ۱ $$
به این ترتیب، به تابعی که با گرفتن عدد ۱، زاویه ۴۵ درجه را به ما میدهد، تابع ارک تانژانت ۱ میگوییم و آن به صورت زیر نمایش میدهیم:
$$ arctan ۱ = ۴۵ ^ { circ } $$
محاسبه آرک تانژانت، دقیقا بر اساس همین مفهوم صورت میگیرد.
تعریف هندسی ارک تانژانت
توابع مثلثاتی، توابعی هستند که رابطه بین اضلاع و زاویههای یک مثلث قائمالزاویه را نمایش میدهند. از اینرو، نمایش هندسی توابع مثلثاتی، معمولا با استفاده از رسم یک مثلث قائمالزاویه انجام میشود. برای تعریف هندسی مفهوم ارک تانژانت، مثلث قائمالزاویه زیر را در نظر بگیرید.
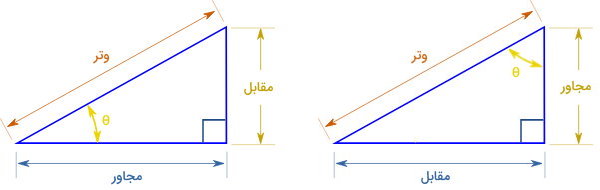
بر اساس اندازه ضلعها و زاویههای این مثلث، نسبتهای مثلثاتی به صورت زیر تعریف میشوند:
نسبت ضلع مقابل زاویه θ به وتر = سینوس زاویه θ
نسبت ضلع مجاور زاویه θ به وتر = کسینوس زاویه θ
نسبت ضلع مقابل زاویه θ به ضلع مجاور زاویه θ = تانژانت زاویه θ
فرمول جبری رابطه تانژانت زاویه θ عبارت است از:
$$ tan theta = frac { O } { A } $$
- $$ tan { theta } $$: تانژانت زاویه θ
- O: ضلع مقابل زاویه θ
- A: ضلع مجاور زاویه θ
بر اساس این فرمول، اگر اندازه ضلعهای مقابل و مجاور یک زاویه را داشته باشیم، میتوانیم تانژانت آن زاویه را (بدون دانستن مقدار زاویه) به دست بیاوریم. شاید این سوال برایتان پیش بیاید که برای محاسبه مقدار زاویه باید چه کار کنیم؟ تعیین مقدار زاویه، با استفاده از مفهوم آرک تانژانت صورت میگیرد. بر اساس پارامترهای بالا، فرمول آرک تانژانت زاویه θ عبارت است از:
$$
arctan left ( frac { O }{ A } right ) = theta
$$
به عبارت دیگر، مقدار زاویه θ برابر با آرک تانژانت نسبت ضلع مقابل زاویه θ به ضلع مجاور زاویه θ است.
مثال: محاسبه اندازه زاویه با استفاده از آرک تانژانت
مثلث قائمالزاویهای را با دو ساق ۴ سانتیمتری در نظر بگیرید. برای تعیین زاویه غیرقائمه در این مثلث، فرمول آرک تانژانت را مینویسیم:
$$
arctan left ( frac { O }{ A } right ) = theta
$$
- $$ { theta } $$: زاویه مجهول
- O: ضلع مقابل زاویه θ برابر با ۴ سانتیمتر
- A: ضلع مجاور زاویه θ برابر با ۴ سانتیمتر
مقادیر معلوم را درون رابطه بالا قرار میدهیم:
$$
arctan left ( frac { ۴ }{ ۴ } right ) = theta
$$
$$
arctan ۱ = theta
$$
در این مثال، زاویه θ برابر با آرک تانژانت ۱ است. بیایید مفهوم آرک تانژانت را برعکس کنیم. یعنی، با استفاده از رابطه بالا، بنویسیم:
$$
tan theta = ۱
$$
همانطور که میبینید، تانژانت زاویه θ برابر با ۱ است. از خود این سوال را بپرسید که تانژانت کدام زاویه برابر با ۱ میشود؟ پاسخ این سوال، زاویه ۴۵ درجه است. به عبارت دیگر، آرک تانژانت ۱، زاویه ۴۵ را نمایش میدهد:
$$ arctan ۱ = ۴۵ ^ { circ } $$
در بخش بعدی از این مطلب مجله فرادرس، بیشتر راجع به روشهای مختلف محاسبه آرک تانژانت صحبت میکنیم.
آرک تانژانت چگونه محاسبه می شود؟
روشهای متعددی برای محاسبه آرک تانژانت وجود دارد. این روشها، یا با استفاده از ماشینحساب یا بدون استفاده از ماشین حساب اجرا میشوند.
روش محاسبه ارک تانژانت با ماشین حساب چیست؟
سادهترین راه برای محاسبه آرک تانژانت، استفاده از ماشینحساب مهندسی است. در ماشینحسابهای مهندسی، دکمهای برای محاسبه تانژانت زوایای مختلف وجود دارد. در بالای این دکمه، معمولا عبارتهایی نظیر $$ tan ^ { – 1 } $$ یا $$ arctan $$ نوشته میشود. به عبارت دیگر، دکمه $$ tan $$ هم برای محاسبه تانژانت و هم برای محاسبه آرک تانژانت مورد استفاده قرار میگیرد.

با فشردن دکمه «SHIFT» یا «2nd»، عملکرد دکمه $$ tan $$، از محاسبه تانژانت به محاسبه آرک تانژانت تغییر میکند.

در صورت فعال بودن SHIFT یا 2nd، با وارد کردن مقدار مورد نظر و فشردن کلید $$ tan $$، تانژانت معکوس آن مقدار محاسبه میشود و به صورت زاویه به نمایش درمیآید. دقت داشته باشید که یکای زاویه نمایش داده شده در ماشینحسابهای مهندسی، معمولا درجه یا رادیان است. در برخی از ماشینحسابهای مهندسی، امکان تنظیم این یکا وجود دارد. اگر این قابلیت در ماشینحساب شما وجود نداشت، از فرمولهای زیر برای تبدیل زاویه از درجه به رادیان و گرادیان استفاده کنید:
$$ radian = frac { degree times pi }{ ۱۸۰ ^ { circ }} $$
$$ gradian = frac { degree times ۴۰۰ }{ ۳۶۰ ^ { circ }} $$
- degree: درجه
- radian: رادیان
- gradian: گرادیان
روش محاسبه ارک تانژانت بدون ماشین حساب چیست؟
محاسبه آرک تانژانت بدون ماشینحساب و با استفاده از فرمولهای ریاضی، کمی پیچیده و زمانبر است. البته اگر برای تعیین مقادیر معروف آرک تانژانت، نیازی به ماشینحساب نیست. به عنوان مثال، آرک تانژانت عدد ۰/۵۷۷، برابر با زاویه ۳۰ درجه است. با حل مثالها و تمرینهای متعدد، بیشتر با این مقادیر آشنا میشوید و هنگام مشاهده آنها، زوایای متناظر آرک تانژانت را به یاد میآورید. جدول زیر، میتواند در محاسبه یا تخمین برخی از مقادیر آرک تانژانت به شما کمک کند.
| تانژانت معکوس | زاویه به درجه | زاویه به رادیان |
| $$ arctan (۰) $$ | $$ ۰ $$ | $$ ۰ ^ { circ } $$ |
| $$ arctan (۰/۰۸۷) $$ | $$ frac { pi } { ۳۶ } approx ۰/۰۸۷ $$ | $$ ۵ ^ { circ } $$ |
| $$ arctan (۰/۱۷۶) $$ | $$ frac { pi } { ۱۸ } approx ۰/۱۷۵ $$ | $$ ۱۰ ^ { circ } $$ |
| $$ arctan (۰/۲۶۸) $$ | $$ frac { pi } { ۱۲ } approx ۰/۲۶۲ $$ | $$ ۱۵ ^ { circ } $$ |
| $$ arctan (۰/۳۶۴) $$ | $$ frac { pi } { ۹ } approx ۰/۳۴۹ $$ | $$ ۲۰ ^ { circ } $$ |
| $$ arctan (۰/۴۶۶) $$ | $$ frac { ۵ pi } { ۳۶ } approx ۰/۴۳۶۳ $$ | $$ ۲۵ ^ { circ } $$ |
| $$ arctan (۰/۵۰۰) $$ | $$ ۰.۴۶۳۶ $$ | $$ ۲۶/۵۶۵ ^ { circ } $$ |
| $$ arctan left ( frac { ۱ }{ sqrt { ۳ } } right ) $$ |
$$ frac { pi } { ۶ } approx ۰/۵۲۴ $$ | $$ ۳۰ ^ { circ } $$ |
| $$ arctan (۰/۷۰۰) $$ | $$ frac { ۷ pi } { ۳۶ } approx ۰/۶۱۱ $$ | $$ ۳۵ ^ { circ } $$ |
| $$ arctan (۰/۸۳۹) $$ | $$ frac { ۲ pi } { ۹ } approx ۰/۶۹۸ $$ | $$ ۴۰ ^ { circ } $$ |
| $$ arctan (۱) $$ | $$ frac { ۳ pi } { ۱۲ } approx ۰/۷۸۵ $$ | $$ ۴۵ ^ { circ } $$ |
| $$ arctan (۱/۱۹۲) $$ | $$ frac { ۵ pi } { ۱۸ } approx ۰/۸۷۳ $$ | $$ ۵۰ ^ { circ } $$ |
| $$ arctan (۱/۴۲۸) $$ | $$ frac { ۱۱ pi } { ۳۶ } approx ۰/۹۶۰ $$ | $$ ۵۵ ^ { circ } $$ |
| $$ arctan (۱/۵) $$ | $$ ۰/۹۸۳ $$ | $$ ۵۶ ^ { circ } $$ |
| $$ arctan left ( sqrt { ۳ } right ) $$ |
$$ frac { pi } { ۳ } approx ۱/۰۴۷ $$ | $$ ۶۰ ^ { circ } $$ |
| $$ arctan (۲) $$ | $$ ۱/۱۰۷ $$ | $$ ۶۳/۴۳۵ ^ { circ } $$ |
| $$ arctan (۲/۱۴۴) $$ | $$ frac { ۱۳ pi } { ۳۶ } approx ۱/۱۳۴ $$ | $$ ۶۵ ^ { circ } $$ |
| $$ arctan (۲/۷۴۷) $$ | $$ frac { ۷ pi } { ۱۸ } approx ۱/۲۲۲ $$ | $$ ۷۰ ^ { circ } $$ |
| $$ arctan (۳) $$ | $$ ۱/۲۴۹ $$ | $$ ۷۱ ^ { circ } $$ |
| $$ arctan (۳/۷۳۲) $$ | $$ frac { ۵ pi } { ۱۲ } = ۱/۳۰۹ $$ | $$ ۷۵ ^ { circ } $$ |
| $$ arctan (۵/۶۷۱) $$ | $$ frac { ۴ pi } { ۹ } approx ۱/۳۹۶ $$ | $$ ۸۰ ^ { circ } $$ |
| $$ arctan (۱۱/۴۳۰) $$ | $$ frac { ۱۷ pi } { ۳۶ } approx ۱/۴۸۴ $$ | $$ ۸۵ ^ { circ } $$ |
| $$ arctan (infty) $$ | $$ infty $$ | $$ ۹۰ ^ { circ } $$ |
مقادیر جدول بالا، بر اساس ربع اول دایره مثلثاتی نوشته شدهاند. برای ربع چهارم، دقیقا همین مقادیر را اما با علامت منفی داریم. آرک تانژانت، در ربعهای دوم و سوم تعریف نمیشود. در بخش دامنه و برد آرک تانژانت، به توضیح این موضوع میپردازیم.

دیگر روش های محاسبه آرک تانژانت
از دیگر روشهای محاسبه آرک تانژانت میتوان به موارد زیر اشاره کرد:
- محاسبه آرک تانژانت با ماشین حساب ویندوز: برنامه Calculator را باز کنید. حالت ماشین حساب را بر روی Scientific قرار دهید. پس از وارد کردن مقدار دلخواه، بر روی Trigonometry و سپس 2nd کلیک کنید. در نهایت، با انتخاب $$ tan { – ۱ } $$، آرک تانژانت مقدار مورد نظر را به دست بیاورید.
- محاسبه آرک تانژانت در اکسل: عبارت =ATAN(
را در نوار فرمولنویسی اکسل بنویسید و پس از وارد کردن مقدار مورد نظر، پرانتز را ببندید. با فشردن کلید Enter، آرک تانژانت عدد وارد شده به دست میآید.
- محاسبه آرک تانژانت به صورت آنلاین: به سایتهای تخصصی انجام محاسبات ریاضی مانند Symbolab (+) یا Wolfram Alpha (+) بروید. با استفاده از ابزارهای فرمولنویسی در این سایتها، آرک تانژانت مقادیر مورد نظر خود را تعیین کنید.
- محاسبه آرک تانژانت با سری تیلور: از فرمول $$ tan ^ { -۱ } ( x ) = x – frac {x ^ ۳}{ ۳ } + frac { x ^ ۵ }{ ۵ } – frac { x ^ ۷ }{ ۷ } + … $$ برای محاسبه آرک تانژانت مقادیر مورد نظر ($$ x $$) کمک بگیرید.
- محاسبه آرک تانژانت به روش هندسی: یک مثلث قائمالزاویه را به نحوی رسم کنید که نسبت ساقهای آن برابر با عدد درون تانژانت معکوس شود. سپس، با استفاده از نقاله، اندازه زوایای مثلث را به دست بیاورید.
دامنه و برد ارک تانژانت چیست ؟
دامنه و برد تابع، مقادیر مجاز ورودی و خروجی تابع را نمایش میدهند. دامنه یا مجموعه ورودیهای مجاز تابع $$ arctan ( x ) $$، مجموعه اعداد حقیقی است. بنابراین، هر عدد حقیقی را میتوان در این تابع قرار داد. با این وجود، برد یا مجموعه خروجیهای تابع $$ arctan ( x ) $$، به بازه باز $$ left ( – frac {pi }{ ۲ } , frac {pi }{ ۲ } right ) $$ محدود میشود. به عبارت دیگر، $$ arctan ( x ) $$ نمیتواند هیچ جوابی خارج از این بازه داشته باشد.
برای تعیین دامنه و برد تابع آرک تانژانت، از دامنه و برد تابع تانژانت کمک میگیریم. تابع تانژانت را میتوانیم به صورت زیر تعریف کنیم:
$$ tan ( x ) = frac { sin ( x ) }{ cos ( x ) } $$
برای تعیین دامنه، باید مقادیری را در نظر بگیریم که استفاده از آنها به عنوان ورودی تابع ($$ x $$) مانعی نداشته باشد. بر اساس رابطه بالا، نمیتوانیم از $$ x = ۰ $$ در تابع $$ tan ( x ) $$ استفاده کنیم. زیرا با این کار، مخرج کسر برابر با صفر و خروجی تابع، تعریف نشده میشود. بنابراین، دامنه تابع $$ tan ( x ) $$، مجموعه اعداد حقیقی، به غیر از عدد ۰ است. خروجی $$ tan ( x ) $$ برای مقادیر موجود در این دامنه، از منفی بینهایت تا مثبت بینهایت تغییر میکند. در نتیجه، برد $$ tan ( x ) $$، مجموعه اعداد حقیقی است.
تمام توابع مثلثاتی از جمله تابع تانژانت، از توابع چند به یک هستند. معکوس یک تابع، تنها زمانی وجود خواهد داشت که رابطه بین ورودیها و خروجیهای آن، یک به یک و پوشا باشد. از طرفی، میدانیم که دامنه توابع مثلثاتی، برد توابع مثلثاتی معکوس بوده و برد توابع مثلثاتی، دامنه توابع مثلثاتی معکوس است. به همین دلیل، برای به دست آوردن دامنه و برد تابع آرک تانژانت، مجبور هستیم ابتدا بر روی دامنه تابع تانژانت، یک محدودیت اعمال کنیم. اگر بازه باز $$ left ( – frac {pi }{ ۲ } , frac {pi }{ ۲ } right ) $$ (به غیر از عدد ۰) را به عنوان دامنه تابع تانژانت در نظر بگیریم، تغییری در محدوده برد رخ نمیدهد. به این ترتیب، دامنه $$ arctan ( x ) $$، برابر با مجموعه اعداد حقیقی و برد آن برابر با بازه باز $$ left ( – frac {pi }{ ۲ } , frac {pi }{ ۲ } right ) $$ میشود.

نمودار آرک تانژانت به چه شکل است؟
برای رسم نمودار آرک تانژانت، ابتدا دستگاه محورهای مختصات x-y را رسم میکنیم. سپس، دامنه و برد این تابع را در نظر میگیریم. تابع آرک تانژانت به صورت زیر نوشته میشود:
$$ y = arctan ( x ) $$
مختصات چندین نقطه از تابع بالا را به دست میآوریم:
$$
x = infty to y = frac { pi }{ ۲ }
$$
$$
x = sqrt { ۳ } to y = frac { pi }{ ۳ }
$$
$$
x = ۰ to y = ۰
$$
$$
x = – sqrt { ۳ } to y = – frac { pi }{ ۳ }
$$
$$
x = – infty to y = – frac { pi }{ ۲ }
$$
اگر این نقاط را درون دستگاه محورهای مختصات مشخص کرده و آنها را به یکدیگر وصل کنیم، نموداری مشابه تصویر زیر به دست میآید.

مشتق ارک تانژانت چیست ؟
مشتق آرک تانژانت، شیب مماس بر منحنی این تابع در یک نقطه مشخص است. فرمول مشتق آرک تانژانت به صورت زیر نوشته میشود:
$$
frac { d } { d x } arctan ( x ) = frac { ۱ } { ۱ + x ^ ۲ }
$$
فرم عمومیتر فرمول مشتق آرک تانژانت عبارت است از:
$$
frac { d } { d x } arctan ( u ) = frac { u ^ { prime } } { ۱ + u ^ ۲ }
$$
در فرمول بالا، $$ u $$، تابعی از متغیر $$ x $$ است.
اثبات فرمول مشتق آرک تانژانت
برای اثبات فرمول مشتق $$ arctan ( x ) $$، تابع زیر را در نظر بگیرید:
$$ y = arctan ( x ) $$
هر دو طرف رابطه بالا را درون تابع تانژانت قرار دهید:
$$
tan ( y ) = tan ( arctan ( x ) )
$$
میدانیم:
$$
tan ( arctan ( x ) ) = x
$$
بنابراین:
$$
tan ( y ) = x
$$
اکنون، از هر دو طرف رابطه بالا، بر حسب $$ x $$ مشتق میگیریم:
$$
frac { d } { d x } tan ( y ) = frac { d } { d x } x
$$
مشتق تانژانت برابر است با:
$$
frac { d } { d x } tan ( y ) = sec ^ ۲ ( y )
$$
بر اساس قواعد مشتق جزئی، داریم:
$$
frac { d y } { d x } sec ^ ۲ ( y ) = ۱
$$
$$
frac { d y } { d x } = frac { ۱ } { sec ^ ۲ ( y ) }
$$
با توجه به اتحادهای مثلثاتی فیثاغورسی، میدانیم:
$$
sec ^ ۲ ( y ) = ۱ + tan ^ ۲ ( y )
$$
به این ترتیب، خواهیم داشت:
$$
frac { d y } { d x } = frac { ۱ } { ۱ + tan ^ ۲ ( y ) }
$$
در مراحل قبل، نشان دادیم:
$$
tan ( y ) = x
$$
در نتیجه:
$$
frac { d y } { d x } = frac { ۱ } { ۱ + x ^ ۲ }
$$
یا
$$
frac { d } { d x } arctan ( x ) = frac { ۱ } { ۱ + x ^ ۲ }
$$

انتگرال ارک تانژانت چیست ؟
انتگرال آرک تانژانت، پادمشتق تابع تانژانت معکوس است. این انتگرال، مساحت زیر منحنی آرک تانژانت را نمایش میدهد. فرمول انتگرال آرک تانژانت به صورت زیر نوشته میشود:
$$
int arctan( x ) d x = x arctan ( x ) – frac { ۱ } { ۲ } ln left | ۱ + x ^ ۲ right | + C
$$
ثابت عددی $$ C $$، برای نمایش انتگرال نامعین مورد استفاده قرار میگیرد. مشتق و انتگرال، دو مفهوم مرتبط اما عکس یکدیگر هستند. در بخش قبلی، مشتق آرک تانژانت را معرفی کردیم. اگر از خروجی این مشتق، انتگرال بگیریم، به رابطه زیر میرسیم:
$$
int { frac { ۱ } { ۱ + x ^ ۲ } } d x = arctan ( x ) + C
$$
اثبات انتگرال آرک تانژانت
فرمول انتگرال آرک تانژانت با استفاده از روش انتگرالگیری جز به جز اثبات میشود. بر اساس فرمول انتگرالگیری جز به جز، داریم:
$$ int f ( x ) g ‘ ( x ) d x = f ( x ) g ( x ) – int f ‘ ( x ) g ( x) d x $$
اکنون، تغییر متغیرهای زیر را در نظر بگیرید:
$$ f ( x ) = arctan ( x ) $$
$$ g ^ { prime } ( x ) = ۱ $$
از تابع $$ f ( x ) $$، مشتق گرفته و از تابع $$ g ^ { prime } ( x ) $$، انتگرال میگیریم:
$$
f ^ { prime } ( x ) = frac { d } { d x } arctan ( x ) = frac { ۱ } { ۱ + x ^ ۲ }
$$
$$
g ( x ) = int g ^ { prime } ( x ) d x = int ۱ d x = x
$$
پارامترهای معلوم را درون رابطه انتگرال جز به جز قرار میدهیم:
$$
int (arctan ( x ) times ۱ ) d x = arctan ( x ) times x – int left ( frac { ۱ } { ۱ + x ^ ۲ } times x right ) d x
$$
$$
int arctan ( x ) d x = x arctan ( x ) – int frac { x } { ۱ + x ^ ۲ } d x
$$
انتگرال سمت راست را در ۲ ضرب و تقسیم میکنیم:
$$
int arctan ( x ) d x = x arctan ( x ) – int frac { ۲ x } { ۲ (۱ + x ^ ۲ ) } d x
$$
یکدوم را از درون انتگرال سمت راست بیرون میکشیم:
$$
int arctan ( x ) d x = x arctan ( x ) – frac { ۱ } { ۲ } int frac { ۲ x } { ۱ + x ^ ۲ } d x
$$
جواب انتگرال سمت راست عبارت است از:
$$
int frac { ۲ x } { ۱ + x ^ ۲ } d x = ln | ۱ + x ^ ۲ |
$$
در نتیجه:
$$
int arctan( x ) d x = x arctan ( x ) – frac { ۱ } { ۲ } ln left | ۱ + x ^ ۲ right | + C
$$
اتحادهای آرک تانژانت
در این بخش، به معرفی برخی از خصوصیات و فرمولهای مرتبط با تابع آرک تانژانت میپردازیم. این فرمولها در جدول زیر آورده شدهاند.
| $$ arctan ( – x ) = – arctan ( x ) $$ |
| $$ tan ( arctan x ) = x $$ |
| $$ arctan ( tan x ) = x , for x in left ( – frac { pi } { ۲ }, frac { pi } { ۲ } right ) $$ |
| $$ arctan left ( frac ۱ x right ) = frac pi ۲ – arctan ( x ) = text { arccot} ( x ) , for x > ۰ $$ |
| $$ arctan left ( frac ۱ x right ) = – frac pi ۲ – arctan ( x ) = text { arccot} ( x ) – pi , for x lt ۰ $$ |
| $$ sin ( arctan x ) = frac { x }{ sqrt { ۱ + x ^ ۲} } $$ |
| $$ cos ( arctan x ) = frac { ۱ }{ sqrt { ۱ + x ^ ۲} } $$ |
| $$ arctan ( x ) = ۲ arctan left ( frac { x } { ۱ + sqrt { ۱ + x ^ { ^ { ۲ } } } } right ) $$ |
| $$ arctan ( x ) + arctan ( y ) = arctan left ( frac { x + y }{ ۱ – x y } right ) , if x y lt ۱ $$ |
| $$ arctan ( x ) – arctan ( y ) = arctan left ( frac { x – y }{ ۱ + x y } right ) , if x y gt – ۱ $$ |
| $$ ۲ arctan ( x ) = arcsin left ( frac { ۲ x }{ ۱ + x ^ ۲ }right ), if | x | le ۱ $$ |
| $$ ۲ arctan ( x ) = arccos left ( frac { ۱ – x ^ ۲ }{ ۱ + x ^ ۲ }right ), if x ge ۰ $$ |
| $$ ۲ arctan ( x ) = arctan left ( frac { ۲ x }{ ۱ – x ^ ۲ }right ), if – ۱ lt x lt ۱ $$ |
| $$ arctan ( – x ) = – tan ( x ) , if x in R $$ |
| $$ arctan left ( frac { ۱ }{ x }right ) = – text { arccot } ( x ) , if x gt ۰ $$ |
| $$ arctan ( x ) + text { arccot } ( x ) = frac { pi } { ۲ } $$ |

شاید برایتان جالب باشد که بدانید بین آرک تانژانت و زاویه $$ frac { pi } { ۴ } $$ روابط دیگری برقرار هستند که در جدول زیر آنها را آوردهایم.
| $$ frac { pi } { ۴ } = ۴ arctan left ( frac { ۱ } { ۵ } right ) – arctan left ( frac { ۱ } { ۲۳۹ } right ) $$ |
| $$ frac { pi } { ۴ } = arctan left ( frac { ۱ } { ۲ } right ) + arctan left ( frac { ۱ } { ۳ } right ) $$ |
| $$ frac { pi } { ۴ } = ۲ arctan left ( frac { ۱ } { ۲ } right ) – arctan left ( frac { ۱ } { ۷ } right ) $$ |
| $$ frac { pi } { ۴ } = ۲ arctan left ( frac { ۱ } { ۳ } right ) + arctan left ( frac { ۱ } { ۷ } right ) $$ |
| $$ frac { pi } { ۴ } = ۳ arctan left ( frac { ۱ } { ۴ } right ) + arctan left ( frac { ۱ } { ۲۰ } right ) + arctan left ( frac { ۱ } { ۱۹۸۵ } right ) $$ |
سوالات متداول در رابطه با ارک تانژانت
در آخرین بخش از این مطلب مجله فرادرس، به برخی از پرتکرارترین سوالات مرتبط با مبحث ارک تانژانت و محاسبه آرک تانژانت به طور مختصر پاسخ میدهیم.
تعریف ارک تانژانت چیست ؟
ارک تانژانت، معکوس تابع تانژانت و یکی از توابع معکوس مثلثاتی است.
نام دیگر ارک تانژانت چیست ؟
نام دیگر ارک تانژانت، تانژانت معکوس یا تانژانت وارون است.
عبارت جبری ارک تانژانت چیست ؟
ارک تانژانت با عبارت جبری arctan در روابط ریاضی ظاهر میشود.
عبارت جبری تانژانت معکوس یا وارون چیست؟
تانژانت معکوس یا تانژانت وارون، با عبارت جبری tan^(-۱) (تانژانت به توان منفی یک) در روابط ریاضی ظاهر میشود.
روش محاسبه ارک تانژانت چیست ؟
مقدار آرک تانژانت یا با استفاده از ماشینحساب مهندسی یا بدون ماشینحساب تعیین میشود.
محاسبه آرک تانژانت بدون ماشین حساب چگونه است؟
استفاده از جدول، سایتهای اینترنتی، نرمافزارهای کامپیوتری، فرمولهای ریاضی و ترسیم هندسی، از روشهای محاسبه آرک تانژانت بدون ماشینحساب هستند.
source