ترمودینامیک یکی از بخشهای مهم علم فیزیک است که کاربرد زیادی در زندگی روزمره دارد. با استفاده از این بخش از علم فیزیک، موتور بخار ساخته و یخچال اختراع شد. بنابراین، آشنایی با مفاهیم اولیه قوانین مهم ترمودینامیک بسیار ضروری و لازم است. از اینرو، بسیاری از دانشآموزان در سراسر جهان با این مبحث مهم در درس فیزیک آشنا میشویم. در ایران، دانشآموزان رشتههای ریاضیفیزیک و تجربی با مبحث ترمودینامیک در ترمودینامیک فیزیک دهم آشنا میشوند. دانشآموزان رشته ریاضی در دو فصل و دانشآموزان رشته تجربی در یک فصل، مباحث اصلی ترمودینامیک را مطالعه میکنند.

در این مطلب از مجله فرادرس، ابتدا با اصول و مفاهیم اولیه ترمودینامیک مانند دما، گرما، دماسنج و فرایندهای ترمودینامیکی آشنا میشویم. سپس، در مورد دو قانون اصلی ترمودینامیک صحبت میکنیم. برای درک بهتر این مفاهیم، برخی از مهمترین مسائل ترمودینامیک فیزیک دهم نیز حل شدهاند.
فصل چهارم ترمودینامیک فیزیک دهم
در فصل چهارم از ترمودینامیک فیزیک دهم با مباحث زیر آشنا میشویم:
دما چیست؟
در لیوانی آب سرد و در لیوانی دیگر آب جوش بریزید. این دو لیوان چه تفاوتی با یکدیگر دارند؟ یکی از لیوانها سرد و دیگری داغ است. به بیان دیگر، دمای این دو لیوان متفاوت است. فرض کنید با دوستان خود به گردش رفتهاید. پس از بالا رفتن از کوه و عبور از جنگل به محلی برای استراحت میرسید. ناگهان برف شروع به باریدن میکند و تمام افراد گروه احساس سرما میکنند. برای غلبه بر سرما، پتوها را به دور خود میپیچید و به دور آتش مینشینید. پس از گذشت مدت زمانی مشخص، احساس گرمای مطبوعی به شما دست میدهد. با استفاده از دما میتوانیم میزان سردی و گرمی اجسام مختلف و هوا را مشخص کنیم.
دما توسط دماسنج اندازه گرفته میشود. اساس کار دماسنجها بر مبنای کمیتی به نام متغیر دماسنجی است. این کمیت در برابر تغییر دما تغییر خواهد کرد. رابطه بین دما و متغیر دماسنجی ممکن است مستقیم یا برعکس باشد. همچنین این رابطه با استفاده از چندجملهایها یا تابع توانی تعیین خواهد شد. در هر صورت، متغیر دماسنجی اندازه گرفته میشود. هیچ راهی برای اندازهگیری مستقیم دما وجود ندارد. پس از مشخص کردن متغیر دماسنجی، گام بعدی انتخاب مقیاس دمایی است. اندازهگیری دما بدون انتخاب مقیاس مناسب، معنایی ندارد. ما در دماسنج نیاز به داشتن نقاط ثابت داریم. این نقاط ثابت براساس آزمایشهای تکرارپذیر در دمای مشخص انتخاب میشوند. در واقع در هر دماسنجی حداقل به دو نقطه ثابت و محدوده تعریف شدهای از اعداد نیاز است.
مقیاس اندازه گیری دما چیست؟
در حالت کلی سه مقیاس دمایی وجود دارند:
- سلسیوس
- کلوین
- فارنهایت
مقیاس دمای سلسیوس
درجه سلسیوس واحد اندازهگیری دما در مقیاس سلسیوس است و به طور معمول با عنوان درجه سانتیگراد شناخته میشود. ذکر این نکته مهم است که در این مقیاس فاصله بین نقاط ثابت مرجع ( ۰ و ۱۰۰) به ۱۰۰ درجه تقسیم شده است. از سال ۱۷۴۳ میلادی به بعد نقطه $$0^o$$ مربوط به نقطه انجماد آب و نقطه $$100^o$$ برای نقطه جوش آب در فشار جو در نظر گرفته شدهاند. یکای درجه سلسیوس را با $$^oC$$ نشان داده میشود.

مقیاس دمای فارنهایت
فارنهایت یکی از مقیاسهای دمایی است که از قرن ۱۸ میلادی تاکنون استفاده میشود. این مقیاس توسط «دنیل گابریل فارنهایت» (Daniel Gabriel Fahrenheit) اختراع شد. این یکا با نماد $$^oF$$ نشان داده میشود.
مقیاس دمای کلوین
یکای دیگری به نام کلوین نیز برای اندازهگیری دما وجود دارد که از سال ۱۹۵۴ میلادی به عنوان مقیاس بینالمللی دما انتخاب شد. این یکا با نماد K نشان داده میشود.
تبدیل دما
آسانترین تبدیل دمایی از کلوین به درجه سلسیوس انجام میشود. اندازه دو واحد یکسان و فاصله دمایی یک کلوین برابر با یک درجه سلسیوس است. دمای صفر مطلق در مقیاس کلوین برابر $$0 K$$ و در مقیاس سلسیوس برابر $$-273.15 ^o C$$ است. بنابراین برای تبدیل بین این دو مقیاس عدد $$-273 ^o C$$ نیاز خواهد بود. در ادامه، تبدیل بین این دو مقیاس به زبان ریاضی را مشاهده میکنید:
تبدیل کلوین به سلسیوس
$$ K rightarrow ^o C \ T[ ^o C] = frac{1 ^o C}{1 K}T[k] – 273.15 ^o C \ ^o C = K – 273.15$$
تبدیل سلیوس به کلوین
$$ ^o C rightarrow K \ T[ K ] = frac{1 K }{1 ^o C}T[ ^o C] – 273.15 K \ ^o C = K + 273.15$$
درجه سلسیوس با استفاده از فرمول زیر به درجه فارنهایت تبدیل میشود:
$$(T_{^{circ}text{F}}=frac{9}{5}T_{^{circ}text{C}}+32)
$$
درجه فارنهایت با استفاده از فرمول زیر به درجه سلسیوس تبدیل میشود:
$$T_{^{circ}text{C}}=({^{circ}text{F}}-32) times frac{5}{9}$$
انواع دماسنج
دماسنجها بر اساس مقیاس اندازهگیری درجهبندی شدهاند. همچنین بخش اصلی دماسنج، ماده دماسنجی است. این ماده در دماهای بالا یا پایین واکنش نشان میدهد. جنس ماده دماسنجی به نوع دماسنج بستگی خواهد داشت. دماسنجها انواع مختلفی دارند:
- دماسنج جیوهای: در دماسنج جیوهای از جیوه به عنوان ماده دماسنجی استفاده شده است. جیوه پس از تماس با جسم داغ منبسط میشود و در لوله باریک دماسنج به سمت بالا حرکت میکند. در پایان، جیوه در نقطه مشخصی متوقف خواهد شد. این نقطه، دمای جسم داغ را نشان میدهد.

- دماسنج الکلی: دماسنج الکلی شبیه دماسنج جیوهای است. الکلها در مقایسه با جیوه، نسبت به دما حساستر هستند.

- دماسنج دو فلزی: در این دماسنج مکانیکی از ویژگیهای دو فلز با ضریب انبساطهای متفاوت استفاده میشود. به هنگام تغییر دما، دو فلز، منبسط و از جایگاه خود منحرف میشوند. پس از خمیدگی دو فلز، سوزن درون دماسنج حرکت میکند و دمای اندازهگیری شده را نشان میدهد. از این دماسنج برای اندازهگیری دمای ترموستاتها و فرها استفاده میکنند.

- دماسنج دیجیتالی: از دماسنج دیجیتالی برای اندازهگیری دمای بدن استفاده میشود.

- دماسنج مادون قرمز: به هنگام اندازهگیری دمای جسمی مشخص یا قسمتی از بدن، بدون لمس کردن جسم یا آن قسمت از بدن، از دماسنج مادون قرمز استفاده میشود.

انبساط گرمایی چیست؟
انبساط گرمایی یکی دیگر از مبحثهای ترمودینامیک فیزیک دهم است که در این بخش به اختصار در مورد آن توضیح میدهیم. به طور حتم با این صحنه مواجه شدهاید، شیشه مربایی را از داخل یخچال بیرون میآورید اما نمیتوانید در آن را به راحتی باز کنید. شیشه مربا را مدت کوتاهی زیر آب گرم نگه میدارید و سپس در آن را به راحتی باز میکنید. چرا در شیشه مربا به راحتی باز میشود؟ زیرا با نگه داشتن ظرف مربا زیر آب گرم، حجم آن افزایش مییابد. حجم مواد و اجسام مختلف با افزایش دما، افزایش مییابد. به این عمل انبساط گرمایی گفته میشود. دماسنجها براساس انبساط گرمایی کار میکنند. به عنوان مثال، انبساط الکل در دماسنج الکلی، نمونهای از انبساط گرمایی محسوب میشود.

حجم بیشتر اجسام با افزایش دما، افزایش و با کاهش دما، کاهش مییابد. به هنگام ساخت پلها، ریلهای قطار و بسیاری از سازههای دیگر باید به انبساط گرمایی در اثر تغییر دما توجه شود. به احتمال زیاد از خود پرسیدهاید چرا حجم بیشتر اجسام پس از افزایش دما، افزایش مییابد. اتمها و مولکولها در مواد مختلف، مانند مواد جامد، به طور پیوسته حول نقطه تعادلشان نوسان میکنند. به این حرکت، حرکت گرمایی گفته میشود. هنگامیکه جسمی گرم و دمای آن افزایش مییابد، ذرات تشکیلدهنده آن با سرعت بیشتری حرکت میکنند و میانگین فاصله آنها از ذرات مجاور افزایش مییابد. انبساط گرمایی میتواند، خطی، سطحی یا حجمی باشد.
انبساط خطی چیست؟
میلهای با طول اولیه $$L_1$$ و دمای اولیه $$T_1$$ داریم. دمای میله را تا مقدار $$T_2$$ افزایش میدهیم. بنا بر مشاهدات تجربی، طول میله نیز باید تا مقدار $$L_2$$ افزایش یابد. اگر تغییر دمای میله خیلی زیاد نباشد، تغییر طول آن، $$triangle L = L_2 – L_1$$ را میتوانیم با استفاده از رابطه زیر بهدست آوریم:
$$triangle L = alpha L_1 triangle T$$
در رابطه فوق:
- $$alpha$$ ضریب انبساط طولی میله و یکای اندازهگیری آن $$frac { 1 } { K }$$ یا $$frac { 1 } { ^o C }$$ است. مقدار ضریب انبساط طولی به جنس میله بستگی دارد.
- $$triangle L$$ و $$L_1$$ به ترتیب تغییر طول و طول اولیه میله هستند و یکای اندازهگیری آنها متر است. این بدان معنا است که طول برحسب سانتیمتر یا میلیمتر باید به متر تبدل شوند.
- $$triangle T$$ تغییر دما و یکای اندازهگیری آن کلوین یا درجه سلسیوس است.
انبساط سطحی چیست؟
جسمی با مساحت اولیه $$A_1$$ و دمای اولیه $$T_1$$ داریم. دمای جسم را تا مقدار $$T_2$$ افزایش میدهیم. بنا بر مشاهدات تجربی، مساحت جسم نیز باید تا مقدار $$A_2$$ افزایش یابد. تغییر مساحت جسم، $$triangle A = A_2 – A_1$$ را میتوانیم با استفاده از رابطه زیر بهدست آوریم:
$$triangle A = 2 alpha A_1 triangle T$$
در رابطه فوق:
- $$alpha$$ ضریب انبساط طولی جسم و یکای اندازهگیری آن $$frac { 1 } { K }$$ یا $$frac { 1 } { ^o C }$$ است.
- $$triangle A$$ و $$A_1$$ به ترتیب تغییر مساحت و مساحت اولیه جسم هستند و یکای اندازهگیری آنها مترمربع است.
- $$triangle T$$ تغییر دما و یکای اندازهگیری آن کلوین یا درجه سلسیوس است.

انبساط حجمی چیست؟
جسمی با حجم اولیه $$A_1$$ و دمای اولیه $$T_1$$ داریم. دمای جسم را تا مقدار $$T_2$$ افزایش میدهیم. بنا بر مشاهدات تجربی، حجم جسم نیز باید تا مقدار $$V_2$$ افزایش یابد. تغییر حجم جسم، $$triangle V = V_2 – V_1$$ را میتوانیم با استفاده از رابطه زیر بهدست آوریم:
$$triangle V = beta V_1 triangle T$$
در رابطه فوق، $$beta$$ ضریب انبساط حجمی جسم است. افزایش حجم بیشتر مواد جامد به هنگام افزایش دما در تمام راستاها به صورت یکسان انجام میشود. بنابراین، در حالت کلی ضریب انبساط حجمی، $$beta$$، سه برابر ضریب انبساط طولی، $$beta$$، است:
$$beta = 3 alpha$$
تا اینجا با مفاهیمی مانند دما و و انبساط گرمایی از ترمودینامیک فیزیک دهم آشنا شدیم. در ادامه، در مورد انبساط غیر عادی آب صحبت میکنیم.
انبساط غیر عادی آب
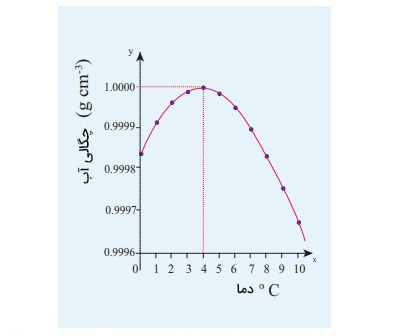
در حالت کلی، بیشتر مواد با افزایش دما منبسط میشوند و چگالی آنها کاهش مییابد. همچنین، با کاهش دما حجم ماده کاهش و چگالی آن افزایش خواهد یافت. اما آب رفتار متفاوتی نسبت به دما از خود نشان میدهد. رفتار آب تا دمای ۴ درجه سانتیگراد مشابه تمام مواد دیگر است. چگالی آب با سرد شدن آن افزایش مییابد. با کاهش دما تا ۴ درجه سانتیگراد، چگالی آب به بیشینه مقدار خود میرسد. با کاهش بیشترِ دمای آب، رفتار متفاوتی را از آن مشاهده میکنیم. با کاهش بیشتر دما و رسیدن آن به مقدار صفر درجه سلسیوس، حجم آب افزایش و چگالی آن کاهش مییابد.
گرما چیست؟
در زندگی روزمره، بارها با کلمه گرما روبرو شدهاید و آن را احساس کردهاید. به عنوان مثال، هنگامی که لیوانی چای داغ را در دست میگیرید، گرمای آن را احساس خواهید کرد یا در یکی از روزهای گرم مرداد ماه با خود میگویید، چه هوای گرمی. گرما مفهومی است که در بسیار از مبحثهای فیزیک، مانند فیزیک گرما و ترمودینامیک، استفاده میشود. فنجان قهوه داغی را با دمای ۹۰ درجه سلسیوس در نظر بگیرید. فرض کنید دمای محیط نیز برابر ۳۰ درجه سلسیوس باشد. چه اتفاقی رخ میدهد؟ همانطور که بارها مشاهده کردهاید فنجان قهوه به تدریج سرد و با دمای اتاق برابر میشود. در این حالت میگوییم قهوه و هوای اتاق به تعادل گرمایی رسیدهاند.
در مقیاس ماکروسکوپی میگوییم گرما از فنجان قهوه به محیط اطراف منتقل میشود. حقیقت آن است که گرما از قهوه به محیط اطراف منتقل میشود و دمای قهوه و انرژی آن کاهش مییابد. به انتقال انرژی از جسم داغ به جسم سرد، گرما میگوییم.
ظرفیت گرمایی چیست؟
به مقدار انرژی گرمای لازم برای افزایش دمای جسمی مشخص به اندازه یک درجه سلسیوس، ظرفیت گرمایی گفته میشود. ظرفیت گرمایی یکی دیگر از مباحث مهم ترمودینامیک فیزیک دهم است. مواد مختلف، پاسخهای متفاوتی به گرما میدهند. صندلی فلزی خود را در یک روز آفتابی و گرم، زیر نور خورشید قرار دهید. پس از مدتی با لمس صندلی متوجه داغی سطح آن میشوید. حال مقداری آب با جرمی برابرِ جرم صندلی فلزی را در برابر نور خورشید قرار دهید. پس از مدت زمان مشابه خواهید دید که دمای آب به اندازه دمای صندلی فلزی بالا نرفته است. این بدان معنا است که ظرفیت گرمایی آب با ظرفیت گرمایی صندلی فلزی برابر نیست و آب ظرفیت گرمایی بالاتری دارد. دمای آب به آسانی افزایش نمییابد، اما به راحتی میتوانیم دمای فلزات را افزایش دهیم.

به مقدار انرژی گرمایی لازم برای افزایش دمای یک گرم از مادهای مشخص به اندازه یک درجه سلسیوس، گرمای ویژه گفته میشود. گرمای ویژه با c و ظرفیت گرمایی با C نشان داده میشوند. واحد اندازهگیری گرمای ویژه برابر ژول بر گرم بر درجه سانتیگراد ($$mathrm{J} / mathrm{g}^{circ} mathrm{C}$$) یا کالری بر گرم بر درجه سانتیگراد ($$mathrm{cal} / mathrm{g}^{circ} mathrm{C}$$) است. جسم دلخواهی را در نظر بگیرید که با محیط اطراف خود مقداری گرما به اندازه Q مبادله و به همین دلیل دمای جسم از مقدار $$T_1$$ به $$T_2$$ تغییر میکند. مقدار گرمای مبادله شده بین جسم و محیط اطراف آن با تغییرات دمای جسم متناسب است و به صورت زیر نوشته میشوند:
$$Q = C triangle T$$
C ظرفیت گرمایی جسم نام و به جنس و جرم جسم بستگی دارد. ظرفیت گرمایی با استفاده از رابطه زیر به گرمای ویژه مربوط میشود:
$$c = frac { C } { m }$$
رابطه فوق را در رابطه $$Q = C triangle T$$ قرار میدهیم. بنابراین، گرمای مبادله شده بین جسم و محیط به صورت زیر نوشته میشود:
$$Q = mc triangle T$$
گرمای ویژه هر جسمی به جنس ماده سازنده جسم و دمای آن بستگی دارد.
دمای تعادل چیست؟
دو جسم A و B با دماهای متفاوت را در نظر بگیرید که در تماس با یکدیگر قرار دارند. پس از گذشت مدت زمانی مشخص، دو جسم به دمای یکسانی میرسند. در ابتدا دمای دو جسم متفاوت و دمای جسم A بزرگتر از دمای جسم B است. بنابراین، گرما از جسم A به B منتقل میشود. این انتقال گرما تا برابر شدن دمای دو جسم ادامه مییابد. به دمایی که دو جسم پس از مدتی به آن میرسند، دمای تعادل گفته میشود. مقدار آن را میتوانیم با استفاده از قانون پایستگی انرژی بهدست آوریم. توجه به این نکته مهم است که تعداد اجسام در تماس با یکدیگر میتواند بیشتر از دو باشد.
گرما از جسمی با دمای بالاتر به جسمی با دمای کمتر منتقل میشود. بر طبق قرارداد، Q برای اجسامی که گرما میگیرند، مثبت و برای اجسامی که گرما از دست میدهند، منفی در نظر گرفته میشود. فرض کنید دو جسم یک و دو با یکدیگر در تماس هستند و گرما از جسم یک به جسم دو منتقل میشود. بر طبق قانون بقای انرژی، تمام گرمای خارج شده از جسم یک به جسم دو منتقل میشود:
$$Q_1 + Q_2 = 0$$
اگر بیشتر از دو جسم با یکدیگر در تماس باشند، رابطه فوق را میتوان به صورت زیر گسترش داد:
$$Q_1 + Q_2 + Q_3 + .. = 0$$

فرض کنید تعدادی جسم با جرمهای $$m_1$$ و $$m_2$$ و $$m_3$$ و …، گرماهای ویژه $$c_1$$ و $$c_2$$ و $$c_3$$ و … و دماهای اولیه $$theta _ 1$$ و $$theta_2$$ و $$theta_3$$ و … در تماس با یکدیگر قرار دارند. دماهای این اجسام پس از مدتی با یکدیگر برابر میشوند. دمای تعادل، $$theta$$، را میتوانیم با استفاده را از رابطه زیر بهدست آوریم:
$$m_1 c_1left(theta-theta_1right)+m_r c_rleft(theta-theta_rright)+m_r c_rleft(theta-theta_rright)+ldots=0$$
گرماسنج و گرماسنجی
گرماسنج (کالریمتر) ظرفی است که به خوبی از نظر گرمایی عایقبندی شده است و از آن برای اندازهگیری گرمای ویژه اجسام مختلف استفاده میشود. برای اندازهگیری گرمای ویژه جسمی توسط گرماسنج، مرحلههای زیر را طی میکنیم:
- مقدار آب با جرم معین داخل گرماسنج میریزیم.
- پس از رسیدن آب و گرماسنج به دمایی یکسان، دمای آب را اندازه میگیریم.
- جسمی با جرم و دمای اولیه مشخص را درون گرماسنج قرار میدهیم.
- برای آنکه مجموعه گرماسنج، آب و جسم زودتر به دمای تعادل برسد، آب را هم میزنیم.
- پس از رسیدن مجموعه به دمای تعادل، مقدار آن را به صورت زیر محاسبه میکنیم:
$$Q_{ water } + Q_ { object } + Q_ { cal } = 0 \ m _ { waer } c_ { water } ( theta – theta_ { 1 water } ) + m_ { object } c_ { object } ( theta – theta _ { 1 object } ) + m _ { cal } c _ cal ( theta – theta _ { 1 cal } ) = 0$$
تغییر حالت های ماده
ماده حالتهای مختلفی (فازهای مختلفی) مانند جامد، مایع و گاز دارد. به طور معمول، مواد با دریافت یا از دست دادن گرما از حالتی به حالت دیگر تغییر میکنند. در این بخش از ترمودینامیک فیزیک دهم در مورد انواع تغییر حالت های ماده صحبت میکنیم.
تبدیل حالت مایع به جامد
نوشیدن آب خنک در گرمای تابستان بسیار لذتبخش است. آب را میتوانیم به کمک قالبهای کوچک یخ خنک کنیم. سوالی که ممکن است مطرح شود آن است که قالبهای جامد یخ چگونه تشکیل شدهاند؟ برای انجام این کار، ظرفی را از آب پر میکنیم و آن را داخل یخچال فریزر با دمای بسیار کم قرار میدهیم. گرما بین آب داخل ظرف و هوای سرد داخل فریزر مبادله و از جسمی با دمای بالاتر به جسمی با دمای پایینتر منتقل میشود. انتقال گرما تا جایی ادامه مییابد که هیچ انرژی برای حرکت ذرات نسبت به یکدیگر وجود نداشته باشد.

در این حالت، آب مایع به یخ جامد تبدیل شده است. به فرایند تبدیل آب مایع به یخ جامد، انجماد گفته میشود. به دمای تبدیل مایع به جامد، دمای انجماد میگوییم. نقطه انجماد، دمایی است که در آن مایع در فشار اتمسفر، از حالت مایع به جامد تبدیل میشود.
تبدیل حالت جامد به مایع
فرایندی که در آن ماده جامد با اضافه کردن گرما به مایع تبدیل میشود، ذوب نام دارد. به عنوان مثال، تکههای کوچک یخ با قرار گرفتن در دمای اتاق، ذوب میشوند. به دمایی که در آن ماده جامد با گرفتن گرما به مایع تبدیل میشود، نقطه ذوب میگوییم. این اتفاق در فشار یک اتمسفر رخ میدهد. در نقطه ذوب، دو فاز مایع و جامد در حالت تعادل در کنار یکدیگر قرار دارند. به مقدار گرمای لازم بر حسب ژول برای تبدیل جامد به مایع در نقطه ذوب و در دمای ثابت، گرمای نهان ذوب گفته میشود. گرمای نهان ذوب برابر مقدار انرژی لازم برای تبدیل ماده از حالت جامد به مایع در دمای ثابت است و با استفاده از فرمول زیر بهدست میآید:
$$Q = m L_F$$

در رابطه فوق:
- $$Q$$ برابر مقدار انرژی جذب شده برای تبدیل ماده از مایع به جامد است و بر حسب ژول یا کالری اندازه گرفته میشود.
- $$m$$ جرم است و بر حسب کیلوگرم اندازه گرفته میشود.
- $$L_F$$ گرمای ویژه نهان ذوب است.
توجه به این نکته مهم است که اگر تغییر فاز مایع به جامد انجام شود، ماده گرما از دست خواهد داد و مقدار گرمای از دست داده برابر است با:
$$Q = – m L_F$$
تبدیل حالت گاز به مایع
به هنگام دوش آبِ گرم در حمام بسته، آینه داخل حمام مهآلود میشود. قسمتی از آبِ داغِ دوش به بخار تبدیل و در تماس با سطوح سرد، مانند آینه داخل حمام، سرد میشود و انرژی از دست میدهد. ذرات آبِ سرد شده دیگر انرژی لازم برای غلبه بر نیروی جاذبه را ندارند. بنابراین به یکدیگر نزدیک و قطرات آب را تشکیل میدهند. به فرایند تبدیل گاز به مایع، میعان میگوییم.
تبدیل حالت مایع به گاز
اگر آب را به اندازه کافی گرم کنیم، شروع به جوشیدن میکند. حبابهای بخار آب در آب جوش تشکیل میشوند. این حالت به این دلیل رخ میدهد که مولکولهای تشکیلدهنده آب، انرژی کافی برای غلبه بر نیروی جاذبه بین یکدیگر بهدست میآورند به حالت گازی (بخار) تبدیل میشوند. به فرایندی که طی آن مایع میجوشد و به گاز تبدیل میشود، تبخیر میگوییم. گرمای نهان تبخیر برابر مقدار انرژی لازم برای تبدیل ماده از حالت مایع به گاز در دمای ثابت است و از حاصلضرب جرم جسم در گرمای نهان تبخیر بهدست میآید:
$$Q = m L_V$$

در رابطه فوق:
- $$Q$$ برابر مقدار انرژی جذب شده برای تبدیل ماده از مایع به بخار است و بر حسب ژول یا کالری اندازه گرفته میشود.
- $$m$$ جرم است و بر حسب کیلوگرم اندازه گرفته میشود.
- $$L_V$$ گرمای ویژه نهان تبخیر است.
توجه به این نکته مهم است که اگر تغییر فاز گاز به مایع انجام شود، ماده گرما از دست خواهد داد و مقدار گرمای از دست داده برابر است با:
$$Q = – m L_V$$
روش های انتقال گرما چیست؟
پس از بازگشت از مدرسه، دانشگاه یا سرکار به خانه، غذای باقیمانده از دیشب را از یخچال برداشتهاید و روی اجاق گاز یا داخل فِر گرم کردهاید. قبل از قرار دادن غذا روی گاز یا داخل فِر، با دست زدن به ظرف فهمیدهاید دمای آن پایین است و برای خوردن مناسب نیست. غذا پس از مدتی قرار گرفتن داخل فِر یا روی شعله اجاق گاز، گرم میشود. شاید از خود پرسیده باشید غذا چگونه گرم میشود. به مثال مشابه دیگری توجه کنید. در یکی از روزهای سرد زمستان از بیرون به خانه آمدهاید و احساس سرمای زیادی میکنید. بهترین کار برای گرم کردن چیست؟ کنار بخاری ایستادن. بخاری دمای بالاتری نسبت به بدن شما دارد. با ایستادن کنار بخاری، پس از مدت زمان مشخصی احساس گرمای مطبوعی به شما دست میدهد.
گرم شدن غذا داخل فِر یا گرم شدن شما پس از ایستادن کنار بخاری به دلیل پدیده انتقال گرما یا انتقال حرارت است. انتقال حرارت را میتوان در همه جا مشاهده کرد. به انتقال گرما یا حرارت از نقطهای به نقطه دیگر یا از جسمی به جسم دیگر، انتقال حرارت میگوییم. در مثالهای ذکر شده، گرما از فِر یا اجاق گاز به غذای سرد و از بخاری به دستهای سرد شما منتقل میشود. این بدان معنا است که گرما یا حرارت یکی از انواع انرژی است که از اجسام گرم به اجسام سرد حرکت میکند. حرکت یا انتقال حرارت از اجسام گرم به سرد میتواند از سه طریق رخ دهد:
- هدایتی: انتقال حرارت از طریق هدایت زمانی رخ میدهد که گرما داخل جسم حرکت میکند و از نقطهای به نقطه دیگر میرود. به عنوان مثال، اگر دست خود با دمای کمتر را به فنجان چای با دمای بیشتر بچسبانید، انتقال حرارت را از فنجان به دست خود حس خواهید کرد.

- همرفتی: انتقال حرارت از طریق همرفت یا جابجایی هنگامی رخ میدهد که گرما به دلیل حرکت مایع یا گاز از نقطهای به نقطه دیگر منتقل شود.
- تشعشع: در انتقال حرارت از طریق تشعشع، گرما بین اجسام، بدون آنکه با یکدیگر تماسی داشته باشند، منتقل میشود. به عنوان مثال، اگر در یکی از شبهای سرد زمستان کنار آتش بنشینید، به طور قطع گرمای آتش را حس خواهید کرد یا اگر در یکی از روزهای گرم تابستان، زیر نور خورشید بایستید، گرمای زیادی را حس میکنید.

قوانین گازها
قوانین گازها یکی دیگر از مباحث مهم ترمودینامیک فیزیک دهم است. تمام گازها در شرایط معمولی رفتار مشابهی را از خود نشان میدهند. اما اگر مقدار یکی از مشخصههای گاز مانند فشار، دما یا حجم تغییر بسیار کوچکی کند، رفتار گاز نیز تغییر خواهد کرد. با استفاده از قوانین گازها میتوانیم رفتار گازهای مختلف را پس از تغییر هر مشخصه، بررسی کنیم.
بررسی گاز در فشار ثابت
دانشمندی فرانسوی به نام «ژاک شارل» (Jacques Charles) در سال ۱۷۸۷ میلادی اثر دما بر حجم ماده گازی را در فشار ثابت بررسی کرد. بر طبق یافتههای این دانشمند، در فشار ثابت و در شرایطی که جرم ثابت است، حجم گاز به طور مستقیم با دما متناسب است. این بدان معنا است که با افزایش دما، حجم گاز افزایش و با کاهش دما، حجم گاز کاهش مییابد. نتیجه این آزمایش به صورت زیر نوشته میشود:
$$frac { V } { T } = constant$$
به این نکته توجه داشته باشد که در رابطه فوق، دما برحسب کلوین نوشته میشود. فرض کنید بادکنکی پر شده از هوا دارید. داخل خانه هوا گرم و بیرون از خانه هوا برفی و بسیار سرد است. بادکنک خود را از داخل خانه با دمای بالاتر به بیرون از خانه با دمای پایینتر میبرید. بادکنک فشرده میشود. زیرا حجم هوای داخل بادکنک با کاهش دما، کاهش مییابد.

بررسی گاز در حجم ثابت
شیمیدانی فرانسوی به نام «ژوزف لوئیس گیلوساک» (Gay Lussac) در سال ۱۸۰۲ میلادی به هنگام ساخت دماسنجی هوایی و به صورت تصادفی کشف کرد که در حجم و جرم ثابتِ گازی مشخص، فشار گاز به صورت مستقیم با دما متناسب است.
$$frac { P } { T } = constant$$
به این نکته توجه داشته باشد که در رابطه فوق دما برحسب کلوین نوشته میشود. بطری نوشابهای را در نظر بگیرید. داخل بطری مقدار مشخصی گاز کربندیاکسید با فشار بالا وجود دارد. اگر قوطی نوشابه را در معرض نور خورشید قرار دهید، دمای گاز داخل آن افزایش مییابد. بر طبق قانون گیلوساک، در حجم ثابت، فشار گاز به طور مستقیم با دما تغییر میکند. از اینرو، فشار گاز کربندیاکسید داخل قوطی افزایش مییابد. اگر دمای گاز افزایش چشمگیری داشته باشد، قوطی نوشابه میتواند منفجر شود. اگر فشار و دما به ترتیب از مقدارهای $$P_1$$ و $$T_1$$ به مقدارهای $$P_1$$ و $$T_1$$ تغییر کنند، قانون گیلوساک را میتوان به صورت زیر نیز نوشت:
$$frac { P _ 1 } { T_ 1 } = frac { P _ 2 } { T _2 } $$

بررسی گاز در دمای ثابت
قانون بویل رابطه بین حجم و فشار گاز را در دما و جرمِ ثابت، توضیح میدهد. دانشمندی انگلیسی به نام «رابرت بویل» (Robert Boyle) در سال ۱۶۶۲ میلادی آزمایشی روی گازها به منظور مطالعه رفتار آنها به هنگام تغییرات فیزیکی انجام داد. بر طبق این قانون، با ثابت نگه داشتن دمای گاز، حجم آن با افزایش فشار، کاهش خواهد یافت. به بیان دیگر، با ثابت نگه داشتن دمای گاز، حجم به صورت معکوس با فشار تغییر میکند. به این نکته توجه داشته باشید که در این حالت، تعداد مولکولهای گاز نیز باید ثابت باشند:
$$begin{gathered}
mathrm{p} propto 1 / mathrm{V} \
mathrm{p}=mathrm{k}_1 1 / mathrm{V}
end{gathered}$$
در رابطه فوق، $$k_1$$ ثابت تناسب دارد و میتواند به صورت زیر نیز نوشته شود:
$$k_1 = PV$$
اگر گازی با جرم ثابت در دمای ثابت منبسط شود، به حجم و فشار نهایی $$V_2$$ و $$P_2$$ میرسد. اگر فشار و حجم اولیه گاز به ترتیب برابر $$P_1$$ و $$V_1$$ باشند، بر طبق قانون بویل داریم:
$$mathrm{p}_1 times mathrm{V}_1=mathrm{p}_2 times mathrm{V}_2=operatorname{constant}left(mathrm{k}_1right)$$
رابطه فوق را به صورت زیر مرتب میکنیم:
$$mathrm{p}_1 / mathrm{p}_2=mathrm{V}_2 / mathrm{V}_1$$
غواصی را در نظر بگیرید که داخل آب شیرجه میزند. هر چه فاصله غواص از سطح آب بیشتر میشود، فشار وارد شده بر او به دلیل وزن آب افزایش مییابد. بر طبق قانون بویل، حجم هوای داخل ریه غواص با افزایش فشار، کاهش مییابد. برعکس، با نزدیک شدن به سطح آب، فشار کاهش و حجم هوا داخل ریه افزایش مییابد.

قانون آووگادرو
در سه قانون بالا جرم گاز را ثابت در نظر گرفتیم. دانشمندی ایتالیایی به نام «آمدئو آووگادرو» (Amedeo Avogadro) در سال ۱۸۱۱ میلادی با ترکیب کردن نتایج بهدست آمده از نظریه اتمی دالتون و قانون گیلوساک، قانون مهم دیگری در گازها را به نام قانون آووگادرو ارائه داد. بر طبق این قانون، در دما و فشار ثابت، حجم تمام گازها از تعداد مساوی مولکول تشکیل شده است. به بیان دیگر، در دما و فشار ثابت، حجم هر گازی به صورت مستقیم با تعداد مولکولهای آن گاز تغییر میکند:
$$mathrm{V} propto mathrm{n}$$
n در رابطه فوق تعداد مولهای گاز را نشان میدهد. تعداد مولکولها در یک مول از هر گازی برابر عددِ ثابت $$6.22 times 10 ^ { 23 }$$ است و عدد آووگادرو نام دارد. مقدارهای دما وفشار را در اینجا مقدارهای استاندارد آنها، یعنی ۲۷۳/۱۵ کلوین و $$10^ 5$$ پاسکال، در نظر میگیریم.
$$N = n N_A enspace and enspace frac { V } { n } = constant$$
در رابطه فوق، n تعداد مول $$N_A$$ همان عدد آووگادرو است. بادکنکی را فرض کنید که با یک مول گاز هلیوم پر شده است. اگر بخواهید بدون تغییر فشار و دما، یک مول گاز هلیوم به بادکنک اضافه کنید، حجم بادکنک دو برابر خواهد شد.

قانون گاز کامل
گاز کامل یکی از مباحث مهم ترمودینامیک فیزیک دهم است. گازها پیچیده هستند. آنها از میلیاردها مولکول گازی پرانرژی ساخته شدهاند که به طور مداوم به یکدیگر برخورد میکنند. از آنجا که توصیف گاز واقعی بسیار سخت و چالشبرانگیز است، مفهومی به نام گاز ایدهال ابداع شد. گاز ایدهال از دو قانون اصلی پیروی میکند:
- مولکولهای گاز ایدهال یکدیگر را جذب یا دفع نمیکنند. این مولکولها، تنها میتوانند به صورت کشسان با یکدیگر یا با دیواره محفظه برخورد کنند.
- مولکولهای تشکیلدهنده گاز ایدهال هیچ فضایی را اشغال نمیکنند. این بدان معنا است که مولکولها در گاز ایدهال به صورت نقطههایی بدون حجم در نظر گرفته میشوند.
شاید با خود فکر کنید، این دو قانون بسیار ایدهال و به دور از واقعیت هستند. بله، هیچ گازی به طور کامل ایدهال نیست. اما با تقریب خوبی بسیاری از گازها را میتوانیم نزدیک به گاز ایدهال در نظر بگیریم. در حقیقت، در دماهای نزدیک به دمای اتاق و در فشارهای نزدیک به فشار اتمسفر، بسیاری از گازها همانند گاز ایدهال رفتار میکنند. گازها را در فشارهای بسیار بالا و دماهای بسیار پایین نمیتوانیم همانند گاز ایدهال در نظر بگیریم. فشار، حجم، و دمای گاز ایدهال با استفاده از فرمولی به نام قانون گاز ایدهال به یکدیگر مربوط میشوند:
$$PV = nRT$$
در رابطه فوق، R ثابت جهانی گازها نام دارد. به هنگام استفاده از این رابطه باید به یکاهای اندازهگیری استفاده شده بسیار دقت کنیم. اگر یکاهای اندازهگیری فشار، حجم و دما به ترتیب برابر پاسکال، مترمکعب و کلوین باشند، مقدار R برابر $$R=8.31 frac{J}{K cdot m o l}$$ است. اگر یکاهای اندازهگیری فشار، حجم و دما به ترتیب برابر اتمسفر، لیتر و کلوین باشند، مقدار R برابر $$R=0.082 frac{L cdot a t m}{K cdot m o l}$$ خواهد بود.
حل مسائل فصل چهارم ترمودینامیک فیزیک دهم
در مطالب بالا با برخی از مفاهیم اولیه ترمودینامیک فیزیک دهم مانند دما، گرما، ظرفیت گرمایی، روشهای انتقال حرارت یا گرما و تغییر حالتهای ماده آشنا شدیم. در این قسمت مسائل مربوط به این مباحث از فیزیک دهم را با یکدیگر حل میکنیم.
مسائل مربوط به دما و دماسنجی فصل چهارم ترمودینامیک فیزیک دهم
در ابتدا دو مسئله در ارتباط با دما و دماسنجی با یکدیگر حل میکنیم.
مسئله ۱
دماهای زیر را برحسب درجه سلسیوس و فارنهایت مشخص کنید:
- صفر کلوین
- $$273 K$$
- $$373 K$$
- $$546 K$$
پاسخ
تمام دماها برحسب کلوین داده شدهاند. برای تبدیل دما برحسب کلوین به دما برحسب درجه سلسیوس و فارنهایت از دو رابطه زیر استفاده میکنیم:
تبدیل کلوین به سلسیوس
$$ K rightarrow ^o C \ T[ ^o C] = frac{1 ^o C}{1 K}T[k] – 273.15 ^o C \ ^o C = K – 273.15$$
تبدیل کلوین به فارنهایت
$$^oF = (K − 273.15) × 1.8 + 32$$
دماهای داده شده برحسب کلوین را در دو رابطه بالا قرار میدهیم و مقدار آنها را برحسب درجه سلسیوس و فارنهایت بهدست میآوریم.
دمای صفر کلوین
$$^o C = K – 273.15 \ ^ o C = 0 – 273.15 $$
در نتیجه، صفر کلوین معادل ۲۷۳/۱۵- درجه سلسیوس است.
$$^oF = (K − 273.15) × 1.8 + 32 \ ^oF = ( 0 − 273.15) × 1.8 + 32 = -459.67 $$
دمای ۲۷۳ کلوین
$$^o C = K – 273.15 \ ^ o C = 273 – 273.15 $$
در نتیجه، صفر کلوین معادل ۰/۱۵- درجه سلسیوس است.
$$^oF = (K − 273.15) × 1.8 + 32 \ ^oF = ( 273 − 273.15) × 1.8 + 32 = 31.775 $$
دمای ۳۷۳ کلوین
$$^o C = K – 273.15 \ ^ o C = 373 – 273.15 $$
در نتیجه، صفر کلوین معادل ۱۰۰/۱۵ درجه سلسیوس است.
$$^oF = (K − 273.15) × 1.8 + 32 \ ^oF = ( 373 − 273.15) × 1.8 + 32 = 212.27 $$
دمای ۵۴۶ کلوین
$$^o C = K – 273.15 \ ^ o C = 546 – 273.15 $$
در نتیجه، صفر کلوین معادل ۲۷۲/۸۵ درجه سلسیوس است.
$$^oF = (K − 273.15) × 1.8 + 32 \ ^oF = ( 546 − 273.15) × 1.8 + 32 = 523.13 $$
مسئله ۲
برای اندازهگیری دما جسمی توسط دماسنج به چه نکاتی باید توجه کنیم؟

پاسخ
به هنگام اندازهگیری دمای جسم با دماسنج باید به نکتههای زیر توجه داشته باشیم:
- قبل از اندازهگیری دما، دماسنج باید به خوبی کالیبره شده باشد. به طور معمول، دماسنج با استفاده از جسمی که دمای آن مشخص است، کالیبره میشود.
- دماسنج باید در مکانی قرار داشته باشد که بتواند به طور دقیق دمای جسم را اندازه بگیرد. در واقع دماسنج نباید تحتتاثیر منبع گرمایی خارجی قرار داشته باشد.
- دماسنج و جسم باید در تماس مستقیم با یکدیگر قرار داشته باشند. در این حالت، گرما میتواند به خوبی بین جسم و دماسنج مبادله شود.
- جسم و دماسنج پس از تماس با یکدیگر، پس از مدت زمان مشخصی به دمای تعادل میرسند. در این حالت میتوانیم دمای جسم را از روی دماسنج بخوانیم.
- محیط، اندازهگیری باید به گونهای باشد که بر دمای اندازهگیری شده توسط دماسنج تاثیر نداشته باشد.
- همانطور که در مطالب بالا دیده شد، دماسنجها انواع متفاوتی دارند. به هنگام اندازهگیری دما باید دماسنج مناسبی انتخاب شود.
- دماسنج باید تمیز باشد.
مسائل مربوط به انبساط گرمایی فصل چهارم ترمودینامیک فیزیک دهم
در ادامه، به منظور آشنایی با مفهوم انبساط گرمایی در ترمودینامیک فیزیک دهم، هشت مسئله را با یکدیگر حل میکنیم.
مسئله ۳
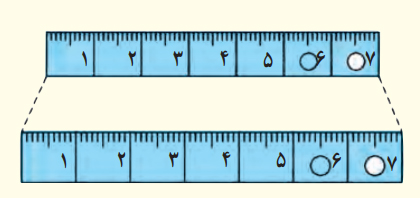
شکل زیر خطکشی فلزی را که در آن سوراخی ایجاد شده است در دو دمای متفاوت نشان میدهد (برای روشن بودن مطلب، انبساط به صورت اغراقآمیزی رسم شده است). از این شکل چه نتیجهای میگیرید؟
پاسخ
با استفاده از تصویر نشان داده شده در صورت مسئله میتوان نتیجه گرفت که خطکش پس از افزایش دما به صورت خطی و یکنواخت منبسط شده است. انبساط گرمایی به این دلیل رخ میدهد که ذرات تشکیلدهنده ماده با افزایش دما سریعتر حرکت میکنند و از یکدیگر دور میشوند. با افزایش دمای خطکش فلزی، اتمها تشکیلدهنده آن با سرعت بیشتری نوسان میکنند و در فاصله بیشتری نسبت به یکدیگر قرار میگیرند.
مسئله ۴
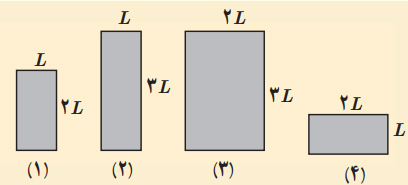
شکل زیر چهار صفحه فلزی همجنس به اضلاع متفاوت را در یک دما نشان میدهد. اگر دمای همه آنها را به اندازه یکسانی افزایش دهیم،
الف) ارتفاع کدام صفحه یا صفحهها افزایش مییابد؟
ب) مساحت کدامیک بیشتر افزایش مییابد؟
پ) اگر در هر چهار تای آنها روزنه کوچک هماندازهای وجود داشته باشد، افزایش قطر چهار روزنه در اثر افزایش دمای یکسان را با هم مقایسه کنید.
پاسخ
همانطور که در تصویر بالا مشاهده میکنید چهار صفحه فلزی همجنس و همدما با مساحتهای مختلف داریم. دمای هر چهار صفحه را به اندازه یکسانی افزایش میدهیم. بنابراین، $$triangle T$$ هر چهار صفحه با یکدیگر برابر است. در قسمت الف میخواهیم بدانیم ارتفاع کدام صفحه یا صفحهها با افزایش دما، بیشتر افزایش مییابد. برای پاسخ به این قسمت از رابطه انبساط خطی استفاده میکنیم:
$$Delta L=alpha L Delta T$$
از آنجا که هر چهار صفحه از فلز یکسانی ساخته شدهاند، ضریب انبساط طولی آنها، $$alpha$$، نیز یکسان است. تغییر ارتفاع هر شکل را جداگانه بهدست میآوریم و با یکدیگر مقایسه میکنیم.
تغییر ارتفاع شکل یک
$$Delta L_1=alpha ( 2 L ) Delta T$$
تغییر ارتفاع شکل دو
$$Delta L_2=alpha ( 3 L ) Delta T$$
تغییر ارتفاع شکل سه
$$Delta L_3=alpha ( 3 L ) Delta T$$
تغییر ارتفاع شکل چهار
$$Delta L_4=alpha ( L ) Delta T$$
با مقایسه تغییر ارتفاع هر چاهر شکل و با توجه به یکسان بودن ضریب انبساط طولی و تغییر دما در آنها، ارتفاع دو صفحه ۲ و ۳ با افزایش دما، بیشتر افزایش پیدا میکند.
در ادامه، قسمت ب را حل میکنیم. در این قسمت باید انبساط سطحی را در نظر بگیریم. افزایش مساحت پس از افزایش دما با استفاده از رابطه زیر بهدست میآید:
$$triangle A = 2 alpha A_1 triangle T$$
تغییر مساحت هر شکل را جداگانه بهدست میآوریم و با یکدیگر مقایسه میکنیم.
تغییر مساحت شکل یک
$$A_1 = 2 L ^ 2 \ triangle A_1 = 2 alpha ( 2 L ^ 2 ) triangle T \ triangle A_1 = 4 alpha L^ 2 triangle T$$
تغییر مساحت شکل دو
$$A_2 = 3 L ^ 2 \ triangle A_2 = 2 alpha ( 3 L ^ 2 ) triangle T \ triangle A_2 = 6 alpha L^ 2 triangle T$$
تغییر مساحت شکل سه
$$A_3 = 6 L ^ 2 \ triangle A_3 = 2 alpha ( 6 L ^ 2 ) triangle T \ triangle A_3 = 12 alpha L^ 2 triangle T$$
تغییر مساحت شکل چهار
$$A_4 = 2 L ^ 2 \ triangle A_4 = 2 alpha ( 2 L ^ 2 ) triangle T \ triangle A_4 = 4 alpha L^ 2 triangle T$$
با توجه به محاسبات انجام شده، مساحت شکل ۳ افزایش بیشتری پیدا میکند. در قسمت پ، روزنه کوچک هماندازهای در هر چهار شکل ایجاد میشود. افزایش قطر چهار روزنه را در اثر افزایش دما با یکدیگر مقایسه میکنیم. فرض کنید قطر هر روزنه قبل از افزایش دما برابر R باشد. در این حالت، قطر روزنهها با افزایش دما به صورت یکسان افزایش مییابد.
مسئله ۵
بزرگراهی از بخشهای بتنی به طول ۲۵/۰ متر ساخته شده است. این بخشها در دمای ۱۰/۰ درجه سانتیگراد، بتنریزی و عمل آورده شدهاند. برای جلوگیری از تاب برداشتن بتن در دمای ۵۰/۰ درجه سانتیگراد، مهندسان باید چه فاصلهای را بین این قطعهها در نظر بگیرند؟ ( $$alpha approx 14 times 10^ { – 6 } K ^ { -1 }$$)

۱/۴ سانتیمتر
۲/۰ سانتیمتر
۱/۸ سانتیمتر
۲/۴ سانتیمتر
انبساط هر قطعه از رابطه زیر بهدست میآید:
$$Delta L_4=alpha ( L ) Delta T$$
مقدارهای داده شده در مسئله را در رابطه فوق قرار میدهیم و تغییر طول هر قطعه را پس از افزایش دما بهدست میآوریم:
$$triangle L = 14 times 10 ^ { -6 } ( frac { 1 } { K }) times ( ( 25.0 m ) times ( 40 frac { 1 } { K } )) = 1.4 times 10 ^ { -2 } m = 1.4 cm$$
به این نکته توجه داشته باشید که باید دماهای داده شده را برحسب کلوین بهدست آوریم. گرچه اختلاف دماهای اولیه و نهایی برحسب درجه سلسیوس و کلوین یکسان است.
مسئله ۶
ظرف آلومینیومی با حجم ۴۰۰ سانتیمتر مکعب در دمای ۲۰/۰ درجه سانتیگراد به طور کامل از گلیسیرین پر شده است. اگر دمای ظرف و گلیسیرین به ۳۰/۰ درجه سانتیگراد برسد، چقدر گلیسیرین از ظرف بیرون میریزد؟

۱/۵۰۰ سانتیمتر مکعب
۱/۶۸۴ سانتیمتر مکعب
۲/۶۸۴ سانتیمتر مکعب
۱/۸۰۰ سانتیمتر مکعب
اگر جسمی با حجم اولیه $$V_1$$ داشته باشیم و دمای آن را از $$T_1$$ به $$T_2$$ افزایش دهیم، تغییر حجم آن برابر است با:
$$triangle V = beta V_ 1 triangle T$$
برای آنکه بدانیم چه مقدار گلیسیرین از ظرف آلومینیومی بیرون میریزد، تغییر حجم ظرف آلومینیومی و گلیسیرین را بهدست میآوریم و آنها را از یکدیگر کم میکنیم. تغییر حجم ظرف آلومینیومی برابر است با:
$$triangle V _ { Al } = beta_ { Al } V_ 1 triangle T \ triangle V _ { Al } = (3 times 21times 10 ^ {-6 } ) times 400 times (30 – 20 ) = 0.276 cm ^ 3$$
تغییر حجم گلیسیرین برابر است با:
$$triangle V _ { g } = beta_ { g } V_ 1 triangle T \ triangle V _ { g } = (0.49times 10 ^ {-3 } ) times 400 times (30 – 20 ) = 1.96 cm ^ 3$$
مقدار گلیسیرینی که از ظرف آلومینیومی پس از افزایش دما بیرون میریزد برابر است با:
$$triangle V_{ g } – triangle V_ { Al } = 1.96 – 0.276 = 1.684 cm ^ 3 $$
مسئله ۷
مقداری بنزین در مخزنی استوانهای به ارتفاع ۱۰ متر ریخته شده است. در دمای ۱۰- درجه سلسیوس فاصله بین سطح بنزین تا بالای ظرف برابر $$triangle h = 50 cm$$ است. اگر از انبساط ظرف در نتیجه افزایش دما چشمپوشی شود، در چه دمایی بنزین از ظرف سرریز میشود؟
۴۵ درجه سلسیوس
۴۲/۶۳ درجه سلسیوس
۵۰/۶۳ درجه سلسیوس
۳۰ درجه سلسیوس
در این مسئله از انبساط ظرف پس از افزایش دما چشمپوشی شده است. بنابراین، با افزایش دما، تنها حجم بنزین افزایش مییابد و پس از رسیدن دما به مقداری مشخص، بنزین از ظرف سرریز میشود. در این مسئله میخواهیم این دما را بهدست آوریم. حجم مخزن استوانه پس از افزایش دما، افزایش نمییابد، بنابراین ارتفاع و سطح مقطح ظرف بدون تغییر باقی میماند. سطح مقطع ظرف ثابت است. در نتیجه، حجم بنزین داخل مخزن با ارتفاع بنزین داخل آن متناسب است. بنابراین، فرمول انبساط حجمی به صورت زیر نوشته میشود:
$$triangle V = beta V_1 triangle T \ A triangle h =beta A h_1 triangle T \ triangle h = beta h_1 triangle T$$
با توجه به آنکه $$triangle h = h _2 – h_1$$، تغییر ارتفاع پس از افزایش دما را میتوانیم به صورت $$h_2 = h_1 ( 1 + beta triangle T )$$ بنویسیم. از آنجا که میخواهیم بدانیم در چه دمایی بنزین از مخزن استوانهای سرریز میشود، رابطه بهدست آمده را برحسب $$T_2$$ مینویسیم:
$$T_2 = frac { triangle h } { beta ( h – triangle h ) } + T _1$$
پس از قرار دادن مقدارهای داده شده در رابطه فوق، دمایی که در آن بنزین از ظرف استوانهای سرریز میشود برابر ۴۲/۶۳ درجه سلسیوس بهدست میآید.
مسئله ۸
در شکل زیر با کاهش دما، نوار دو فلزه به طرف پایین خم میشود. اگر یکی از نوارها برنجی و دیگری فولادی باشد:
الف) نوار بالایی از چه جنسی است؟
ب) اگر نوارها را گرم کنیم به کدام سمت خم میشوند؟

الف: فولاد، ب: با افزایش دما، نوارها به سمت بالا خم میشوند.
الف: برنج، ب: با افزایش دما، نوارها به سمت بالا خم میشوند.
الف: فولاد، ب: با افزایش دما، نوارها به سمت پایین خم میشوند.
الف: برنج، ب: با افزایش دما، نوارها به سمت پایین خم میشوند.
قسمت الف: با کاهش دما، نوار دو فلزه به سمت پایین خم شده است. از آنجا که نوار پایین بیشتر از نوار بالا خمیده شده است، ضریب انبساط نوار پایین باید از ضریب انبساط نوار بالایی بیشتر باشد. با توجه به جدول ضریب انبساط طولی فلزات در فصل چهارم ترمودینامیک فیزیک دهم، ضریب انبساط طولی برنج از فولاد بزرگتر و در نتیجه، فلز بالایی از جنس فولاد و فلز پایینی از جنس برنج است.
قسمت ب: با افزایش دما، نوارها به سمت بالا خم میشوند.
مسئله ۹
طول خطهای لوله گاز، نفت و فراوردههای نفتی در کشورمان که عمدتا مواد سوختی را از جنوب کشور به مرکز و شمال منتقل میکند به چند هزار کیلومتر میرسد. دمای هوا در زمستان ممکن است تا ۱۰- درجه سلسیوس و در تابستان تا ۵۰+ درجه سلسیوس برسد. جنس این لولهها عموما از فولاد با $$alpha approx 10 times 10 ^ { -6 } K ^ { -1 }$$ است. طول خط لوله بین دو ایستگاه تهران – اصفهان تقریبا ۲۳۰ کیلومتر است.
الف) در اثر این اختلاف دما، این خط چقدر منبسط میشود؟
ب) چگونه میتوان تاثیر این انبساط را کمتر کرد؟

الف: مقدار انبساط برابر $$1.42 times 10 ^ 2$$ متر است، ب: با نصب حلقههای انبساط، فاصلهگذاری بین لولهها و عایقبندی مناسب میتوان تاثیر انبساط را کمتر کرد.
الف: مقدار انبساط برابر $$2.42 times 10 ^ 2$$ متر است، ب: با نصب حلقههای انبساط، فاصلهگذاری بین لولهها و عایقبندی مناسب میتوان تاثیر انبساط را کمتر کرد.
الف: مقدار انبساط برابر $$1.36 times 10 ^ 2$$ متر است، ب: با نصب حلقههای انبساط، فاصلهگذاری بین لولهها و عایقبندی مناسب میتوان تاثیر انبساط را کمتر کرد.
الف: مقدار انبساط برابر $$0.42 times 10 ^ 2$$ متر است، ب: با نصب حلقههای انبساط، فاصلهگذاری بین لولهها و عایقبندی مناسب میتوان تاثیر انبساط را کمتر کرد.
قسمت الف: تغییر طول خط لوله نفت بین تهران و اصفهان بین فصلهای تابستان و زمستان برابر است با:
$$triangle L = L_1 = alpha triangle T = ( 10 times 10 ^ { -6 } ) times ( 2.3 times 10 ^ 5 m ) times ( 60 K ) \ = 1.36 times 10 ^ 2 m$$
قسمت ب: انبساط گرمایی در لولههای انتقال نفت را میتوان به روشهای زیر کاهش داد:
- حلقههای انبساط: به طور معمول، بخشی به نام حلقههای انبساط به لولههای نفت افزوده میشود. این بخش انبساط و انقباض لولهها به دلیل تغییر دما را جذب میکند.
- فاصلهگذاری بین لولهها
- عایقبندی مناسب
مسئله ۱۰
در روزی گرم، باری مخزنی حامل سوخت با ۳۰۰۰۰ لیتر بنزین بارگیری شده است. دمای هوا در محل تحویل سوخت ۲۰ درجه سلسیوس کمتر از محلی است که در آنجا سوخ برگیری شده است. راننده چند لیتر سوخت را در این محل تحویل میدهد؟
دمای محل سوختگیری ۲۰ درجه سلسیوس کمتر از محل تحویل سوخت است:
$$triangle V = beta V_1 triangle T \ V_2 = V_1 ( 1 + beta triangle T) \ V_ 2 = (30000 L ) ( 1 + ( 1.00 times 10 ^ { – 3 } ) ( – 20 K ) )\ = 29400 L $$
بنابراین، راننده در حدود ۲۹۴۰۰ لیتر بنزنی به محل مودنظر تحویل میدهد.
مسائل مربوط به گرما فصل چهارم ترمودینامیک فیزیک دهم
تا اینجا، تعدادی مسئله در مورد انبساط گرمایی از ترمودینامیک فیزیک دهم با یکدیگر حل کردیم. در ادامه، چند مسئله در مورد مبحث گرما حل خواهیم کرد.
مسئله ۱۱
برای گرم کردن ۲۰۰ گرم آب جهت تهیه چای، از یک گرمکن الکتریکی غوطهور در آب استفاده میکنیم. روی برچسب گرمکن ۲۰۰ وات نوشته شده است. با نادیده گرفتن اتلاف گرما، زمان لازم برای رساندن آب از ۳۰ درجه سلسیوس به ۱۰۰ درجه سلسیوس را محاسبه کنید.

پاسخ
مقدار زمان لازم برای افزایش دمای آب از ۳۰ درجه سلسیوس به ۱۰۰ درجه سلسیوس برابر است با:
$$Q = mc triangle T , enspace Q = Pt \ Pt = mc triangle T \ 200 W times t = 0.2 kg times 4187 frac { J } { kg. ^o C } ) ( 70 ^o C ) \ t = 293 09 s = 2.94 times 10 ^ 2 s$$
مسئله ۱۲
دمای قطع فلزی ۰/۶۰ کیلوگرمی را توسط گرمکن ۵۰ واتی در مدت ۱۱۰ ثانیه از ۱۸ درجه سلسیوس به ۳۸ درجه سلسیوس رساندهایم. این آزمایش برای گرمای ویژه فلز چه مقداری را میدهد؟ حدس میزنید که این پاسخ از مقدار واقعی گرمای ویژه فلز بیشتر باشد یا کمتر؟
$$458. 33 frac { J } { kg . ^o }$$، کمتر از مقدار واقعی است.
$$458. 33 frac { J } { kg . ^o }$$، بیشتر از مقدار واقعی است.
$$558. 33 frac { J } { kg . ^o }$$، کمتر از مقدار واقعی است.
$$658. 33 frac { J } { kg . ^o }$$، کمتر از مقدار واقعی است.
مقدار زمان لازم برای افزایش دمای فلز از ۱۸ درجه سلسیوس به ۳۸ درجه سلسیوس برابر است با:
$$Q = mc triangle T , enspace Q = Pt \ Pt = mc triangle T \ 50 W times 110 = 0.6 kg times c ( 20 ^o C ) \ c = 458. 33 frac { J } { kg . ^o C}$$
بخشی از گرمای داده شده توسط گرمکن، به هوا و مواد پیرامون فلز منتقل میشود. بنابراین، در رابطۀ $$Q = mc triangle T$$ که برای قطعه فلز به کار میبریم، Q کمتر از Pt خواهد بود. در نتیجه، مقدار واقعی گرمای ویژه فلز، کمتر از پاسخ بهدست آمده است.
مسئله ۱۳
گرماسنجی به جرم ۲۰۰ گرم از مس ساخته شده است. قطعهای ۸۰ گرمی از مادهای نامعلوم همراه با ۵۰ گرم آب، داخل گرماسنج ریخته میشود. اکنون دمای این مجموعه ۳۰ درجه سلسیوس شده است. در این هنگام ۱۰۰ گرم آب ۷۰ درجه سلسیوس را گرماسنج اضافه و دمای تعادل ۵۲ درجه سلسیوس میشود. گرمای ویژه قطعه را محاسبه کنید.

گرمای ویژه ماده مجهول برابر $$600 frac { J } { kg. ^ o C }$$ است.
گرمای ویژه ماده مجهول برابر $$805 frac { J } { kg. ^ o C }$$ است.
گرمای ویژه ماده مجهول برابر $$500 frac { J } { kg. ^ o C }$$ است.
گرمای ویژه ماده مجهول برابر $$705 frac { J } { kg. ^ o C }$$ است.
در این مثال ۴ جسم داریم که با یکدیگر در تعادل گرمایی قرار دارند:
- گرماسنج از جنس مس
- ماده مجهول
- ۵۰ گرم آب ۳۰ درجه سلسیوس
- ۱۰۰ گرم آب ۷۰ درجه سلسیوس
به این نکته توجه داشته باشید که قبل از اضافه شدن آبِ ۷۰ درجه سلسیوس، دمای گرماسنج، ماده مجهول و آبِ برابر ۳۰ درجه سلسیوس است. سپس آب ۷۰ درجه سلسیوس به مجموعه اضافه و پس از مدتی دمای تعادل به ۵۲ درجه سلسیوس میرسد. این بدان معنا است که گرماسنج، ماده مجهول و آب ۳۰ درجه، گرما دریافت میکنند و آب ۷۰ درجه گرما از دست میدهد.
مقدار گرمای دریافت شده توسط گرماسنج
$$Q_ 1 = m c_ { cu } triangle theta = 0.2 kg times ( 386 frac { J } { kg . ^ o C } ) times ( 52 ^oC – 30 ^ o C ) = 1698. 4 J$$
مقدار گرمای دریافت شده توسط آبِ ۳۰ درجه سلسیوس
$$Q_ 2 = m c_ { water } triangle theta = 0.05 kg times ( 4200 frac { J } { kg . ^ o C } ) times ( 52 ^oC – 30 ^ o C ) = 4620 J$$
مقدار گرمای دریافت شده ماده مجهول
$$Q_ 3 = m c_ { unknown } triangle theta = 0.08 kg times ( c ) times ( 52 ^oC – 30 ^ o C ) = 1.76 c$$
مقدار گرمای از دست رفته توسط آب ۷۰ درجه سلسیوس
$$Q_4 = m c_ { water} triangle theta = 0.1 kg times ( 4200 frac { J } { kg . ^ o C } ) times ( 52 ^oC – 70 ^ o C ) = – 7560 J$$
از آنجا که $$Q_1 + Q_2 + Q_3 + Q_4 = 0$$ است، گرمای ویژه ماده مجهول برابر $$705 frac { J } { kg. ^ o C }$$ بهدست میآید.
مسائل مربوط به تغییر حالت های ماده فصل چهارم ترمودینامیک فیزیک دهم
تغییر حالتهای ماده یکی از بخشهای مهم ترمودینامیک فیزیک دهم است. در ادامه، چند مسئله در این مورد حل میکنیم.
مسئله ۱۴
یکی از روشهای بالا بردن دمای جسمی، دادن گرما به آن است. اگر به جسمی گرما دهیم، آیا دمای آن حتما بالا میرود؟ توضیح دهید.
پاسخ
در حالت کلی، دادن گرما به جسم سبب افزایش دمای آن میشود. اما به این نکته توجه داشته باشید که رابطه بین گرما و دما به دلیل عاملهایی مانند تغییر حالت همیشه مستقیم نیست. به عنوان مثال، یخ به هنگام ذوب شدن گرما دریافت میکند، اما دمای آن تا ذوب شدن کامل، ثابت باقی میماند.

مسئله ۱۵
قبل از تزریق دارو یا سرم به بیمار، محل تزریق را با الکل تمیز میکنند. این کار سبب احساس خنکی در محل تزریق میشود. علت را توضیح دهید.
پاسخ
احساس خنکی به دلیل فرایند تبخیر سطحی رخ میدهد. الکل مادهای فرار است، بنابراین با قرار گرفتن در معرض هوا به سرعت تبخیر میشود. از آنجا که الکل از سطح پوست تبخیر میشود، مقداری از گرمای بدن را دریافت میکند. در نتیجه، احساس خنکی به ما دست میدهد.
مسئله ۱۶
کدام گزینه در مورد فرایند ذوب نادرست است؟
الف) افزایش فشار وارد بر جسم در بیشتر مواد، سبب پایین رفتن نقطه ذوب میشود.
ب) افزایش فشار روی یخ، سبب کاهش اندک نقطه ذوب آن میشود.
پ) فرایند ذوب، عملی گرماگیر است.
ت) گرمایی که جسم جامد در نقطه ذوب خود میگیرد تا به مایع تبدیل شود، سبب تغییر دمای آن نمیشود.
برای پاسخ به این پرسش، هر گزینه را به صورت جداگانه بررسی میکنیم:
- گزینه الف: فشار میتواند بر نقطه ذوب ماده تاثیر بگذارد. در بیشتر مواد، افزایش فشار سبب افزایش نقطه ذوب میشود. بنابراین گزینه الف نادرست است.
- گزینه ب: اگر فشار روی یخ افزایش یابد، ذوب آن در دمای پایینتری رخ میدهد. بنابراین، گزینه ب صحیح است.
- گزینه پ: مواد به هنگام تغییر حالت از جامد به مایع، گرما دریافت میکنند. بنابراین، فرایند ذوب عملی گرماگیر و گزینه ب صحیح است.
- گزینه ت: دمای جسم به هنگام تغییر حالت از جامد به مایع، ثابت باقی میماند. بنابراین گزینه ت صحیح است.
مسئله ۱۷
کمترین گرمای لازم برای ذوب کامل ۲۰۰ گرم نقره که در آغاز در دمای ۲۰/۰ درجه سلسیوس قرار دارد، چقدر است؟ (فشار هوا را یک اتمسفر فرض کنید)

$$5.2 times 10 ^ 4 $$ ژول
$$6.2 times 10 ^ 4 $$ ژول
$$4.2 times 10 ^ 4 $$ ژول
$$3.2 times 10 ^ 4 $$ ژول
۲۰۰ گرم نقره در دمای ۲۰ درجه سلسیوس داریم. نقره تا ذوب کامل باید دو مرحله را طی کند:
- ابتدا دمای نقره را با دادن گرما از ۲۰ درجه سلسیوس به ۹۶۰ درجه سلسیوس (نقطه ذوب) میرسانیم. در این حالت، مقدار گرمای لازم برابر است با:
$$Q_1 = mc_{silver} triangle theta = (0.2 kg) (236 frac { kg } { kg. ^oC} ) (960 – 20 ) = 44368 J$$
- پس از رسیدن به نقطه ذوب، دمای نقره علیرغم دادن گرما به آن، تا ذوب کامل ثابت باقی میماند. در این حالت، مقدار گرمای داده شده برابر است با:
$$Q_2 = m L _F = (0.2 kg ) times ( 88.3 times 10^ 3 frac { J } { kg} ) = 17720 J$$
بنابراین، مقدار گرمای لازم برای ذوب کامل ۲۰۰ گرم نقره در دمای ۲۰ درجه سلسیوس برابر است با:
$$Q = Q1 + Q_2 = 44368+17720= 62088 J = 6.2 times 10^ 4 J$$
مسئله ۱۸
یک راه برای جلوگیری از سرد شدن بیش از حد سالنی سربسته در شبهنگام، وقتی که دمای زیر صفر پیشبینی شده است، قرار دادن تشت پر از آب در سالن است. اگر جرم آبِ درون تشت ۱۵۰ کیلوگرم و دمای اولیه آن ۲۰/۰ درجه سلسیوس باشد و همه آن به یخ ۰/۰ درجه سلسیوس تبدیل شود، آب چه مقدار گرما به محیط پیرامونش میدهد؟

$$6.3 times 10 ^ 7 $$ ژول
$$4.3 times 10 ^ 7 $$ ژول
$$2.3 times 10 ^ 7 $$ ژول
$$6.3 times 10 ^ 8 $$ ژول
تشتی از آب با دمای ۲۰/۰ درجه سلسیوس پر شده است. تبدیل این آب به یخ صفر درجه سلسیوس از دو مرحله تشکیل شده است:
- در مرحله اول آبِ ۲۰ درجه سلسیوس با از دست دادن گرما به آبِ صفر درجه تبدیل میشود. مقدار گرمایی که آب از دست میدهد برابر است با:
$$Q_1 = mc_ { water } triangle theta = 150 kg times ( 4200 frac { J } { kg. ^ oC}) times ( 0 -20 ) = -12600000 K = 1.26 times 10 ^ {7 } J$$
- در مرحله دوم، آبِ صفر درجه سلسیوس با از دست دادن گرما به یخ صفر درجه تبدیل میشود. به این نکته توجه داشته باشید که دما ثابت است و تنها تغییر حالت رخ میدهد. مقدار گرمای وارد شده به محیط برابر است با:
$$Q_2 = – m L_f = – ( 150 kg )times 333.7 times 10 ^ 3 frac { J } { kg } = 5. 0 times 10 ^ 7 J$$
مقدار کل گرمای منتقل شده برابر است با:
$$Q = Q_1 + Q_ 2 = – 6.3 times 10 ^ 7 J$$
مسئله ۱۹
۱۰۰ گرم آب درون گرماسنجی ریخته شده است. گرمکنی ۵۰ واتی را درونِ آبِ داخل گرمکن قرار میدهیم.
الف) این گرمکن در مدت یک دقیقه، دمای آب و گرماسنج را از ۲۰ درجه سلسیوس به ۲۵ درجه سلسیوس میرساند. ظرفیت گرمایی گرماسنج را حساب کنید.
ب) چه مدت طول میکشد تا دمای آبِ درون گرماسنج از ۲۵ درجه سلسیوس به نقطه جوش (۱۰۰ درجه سلسیوس) برسد؟
پ) چه مدت طول میکشد تا ۲۰ گرم آبِ در حال جوش درون این گرماسنج به بخار تبدیل شود؟
پاسخ
گرمای دریافتی توسط گرمکن، صرف گرم کردن آب و ظرف گرماسنج میشود:
$$Pt = Q = Q_ { water } + Q_ { cal } \ = m_ {water} c _{water} triangle theta + C_ { cal } triangle theta $$
قسمت الف
گرمکن ۵۰ واتی در مدت یک دقیقه دمای آب را از ۲۰ درجه سلسیوس به ۲۵ درجه سلسیوس میرساند:
$$50 times 60 = 0.1 kg (4200 frac { J } { kg. ^ C } ) ( 25 – 20 ) ^oC + C_ {cal } ( 25 – 20 ) ^oC \ = C_ {cal } = 1.8 times 10 ^ 2 frac { J } { ^oC}$$
قسمت ب
مقدار زمان لازم برای رسیدن دمای آب به ۱۰۰ درجه سلسیوس برابر است با:
$$Pt = m_{water} c_{water} triangle theta + C_ {cal } triangle theta = (0.1) kg ) ( 4200 frac { J} { kg . ^oC } ) times 75 + (1.8 times 10 ^ 2 frac { J } { kg } times 75 ) \ t = frac {45000 J } { 50 } = 900.0 s$$
قسمت پ
از آنجا که آب در حال جوشیدن است، دمای آن افزایش نمییابد. در این حالت، تمام گرمای داده شده به گرماسنج و آب صرف تغییر حالت آب از حالتِ مایع به بخار آب میشود:
$$t = frac { P } { Q } = frac { 50 W } { m L _v } \ t = frac { 50 } { ( 0.02 kg ) (2256 times 10 ^ 3 frac { J } { kg } ) }\ t = 902 s$$
مسئله ۲۰
گرمکنی در هر ثانیه ۲۰۰/۰ ژول گرما میدهد. الف)چقدر طول میکشد تا این گرمکن ۰/۱۰۰ کیلوگرم آبِ ۱۰۰ درجه سلسیوس را به بخار آب ۱۰۰ درجه سلسیوس تبدیل کند؟ ب) این گرمکن در همین مدت، چه مقدار یخ صفر درجه سلسیوس را میتواند به آبِ صفر درجه سلسیوس تبدیل کند؟

پاسخ
ابتدا قسمت الف را حل میکنیم. مقدار گرمای لازم برای آنکه ۰/۱۰۰ کیلوگرم آبِ ۱۰۰ درجه سلسیوس به بخارِ آبِ ۱۰۰ درجه سلسیوس تبدیل شود برابر است با:
$$Q = ml _ V \ Q = 0.1 kg times 2256 times 10 ^ 3 frac { kg } { J } = 2.26 times 10 ^ 5 J $$
گرمکن در هر ثانیه ۲۰۰ ژول گرما میدهد. گرمای لازم برای تبدیل آب ۱۰۰ درجه سلسیوس به بخار آب ۱۰۰ درجه سلسیوس برابر $$2.26 times 10 ^ 5 J$$ است. بنابراین، مدت زمان لازم برای بخار شدن آب ۱۰۰ درجه سلسیوس برابر است با:
$$t = frac { 2.26 times 10 ^ 5 } { 200 } = 1130 s$$
قسمت ب: گرمکن در این مدت زمان، گرمایی برابر $$2.26 times 10 ^ 5 J$$ را به یخ میدهد. مقدار یخی با دمای صفر درجه سلسیوس که میتواند با دریافت این گرما به آبِ صفر درجه سلسیوس تبدیل شود برابر است با:
$$2.26 times 10 ^ 5 J = m times (333.7 times 10 ^ 3 frac { J } { kg } ) \ m = 0.677 kg$$
مسئله ۲۱
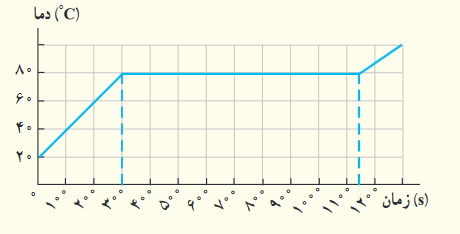
اگر به جسم جامدی که ابعاد آن به اندازه کافی کوچک است، با توان ثابتی گرما بدهیم، نمودار دما-زمان آن به صورت کیفی مانند شکل زیر میشود. این نمودار در اینجا برای جسم جامدی به جرم ۵۰/۰ گرم رسم شده که توسط گرمکنی ۱۰/۰ واتی گرم شده است. الف) چقدر طول میکشد تا این جامد به نقطه ذوب برسد؟ ب) گرمای ویژه جامد و پ) گرمای نهان ذوب آن را بهدست آورید.
پاسخ
نمودار فوق از سه مرحله تشکیل شده است:
- ابتدا دمای جسم در مدت زمان ۳۰۰ ثانیه از ۲۰ درجه سلسیوس به ۸۰ درجه سلسیوس افزایش مییابد.
- سپس، دمای جسم برای مدت زمان مشخصی ثابت باقی میماند.
- در پایان، دمای جسم تا ۱۰۰ درجه سلسیوس افزایش مییابد.
قسمت الف: جسم پس از ۳۰۰ ثانیه به نقطه ذوب خود میرسد.
قسمت ب: گرمای ویژه جامد برابر است با:
$$Q = Pt = mc triangle theta \ P = frac { Q } { t } = frac { mctriangle theta} {t} = frac { 0.05 kg times c times ( 80 – 20) ^oC } { 300 s } \ c = 1000 frac { J } { kg. ^ o C }$$
قسمت پ: گرمای نهان ذوب برابر است با:
$$P = frac { m L _ f } { t } \ 10 W = frac { ( 0.05 kg ) times L _ f } { (1150 s – 300 s ) } \ L _ f = 1.7 times 10 ^ 5 frac { kg } { J } $$
به این نکته توجه داشته باشید که با توجه به نمودار رسم شده، ذوب ماده از ثانیه ۳۰۰ شروع و تا ثانیه ۱۱۵۰ ثانیه ادامه مییابد.
مسئله ۲۲
در چاله کوچکی ۱/۰۰ کیلوگرم آبِ ۰/۰ درجه سلسیوس قرار دارد. اگر بر اثر تبخیر سطحی قسمتی از آن تبخیر شود و بقیه آن یخ ببندد، جرم آبِ یخزده چقدر میشود؟
فرض کنید $$m_1 $$ گرم از آبِ داخلِ چاله بر اثر تبخیر سطحی، تبخیر میشود و $$m_2 $$ گرم از آن یخ میزند. مقدار گرمای لازم برای تبخیر سطحی $$m_1 $$ گرم آب برابر است با:
$$Q_ 1 = m_1 L _ V$$
باقیمانده آب با از دست دادن گرما، یخ میزند. مقدار گرمای از دست داده شده توسط این مقدار آب برابر است با:
$$Q_ 2 = m_2 L_f$$
گرمای لازم برای تبخیر سطحی $$m_1 $$ گرم آب از گرمای از دست رفته توسط $$m_2$$ گرم آبی که یخ میزند تامین میشود:
$$Q_1 = Q_2 \ m_1 K _V = m_2 L _f \ m times 2490 frac { J } { kg . ^ o C } = ( 1- 3 ) times ( 334 frac { J } { kg } { kg. ^ o C } ) $$
با حل معادله بالا، مقدار آبی که تبخیر میشود برابر ۰/۱۱۷ کیلوگرم بهدست میآید. بنابراین، در حدود ۸۸۰ گرم آب، یخ میزند.
مسئله ۲۳
در گروهی از جانوران خونگرم و انسان، تبخیر عرق بدن، یکی از راههای مهم تنظیم دمای بدن است. الف) چه مقدار آب تبخیر شود تا دمای بدنی شخصی به جرم ۵۰/۰ کیلوگرم به اندازه ۱/۰۰ درجه سانتیگراد کاهش یابد؟ گرمای نهان تبخیر آب در دمای بدن (۳۷ درجه سلسیوس) برابر $$2.42 times 10 ^ 6 frac { J } { kg }$$ و گرمای ویژه بدن در حدود ۳۴۸۰ ژول بر کیلوگرم کلوین است. ب) حجم آبی که شخص باید برای جبران آبِ تبخیر شده بنوشد، چه مقدار است؟
الف: ۸۲ گرم، ب: $$7.19 times 10 ^ { -5 }$$ مترمکعب
الف: ۷۲ گرم، ب: $$7.19 times 10 ^ { -5 }$$ مترمکعب
الف: ۷۲ گرم، ب: $$8.19 times 10 ^ { -5 }$$ مترمکعب
الف: ۶۲ گرم، ب: $$7.19 times 10 ^ { -5 }$$ مترمکعب
برای این مسئله فرض میکنیم تمام گرمای لازم برای تبخیر آب، از بدن شخص گرفته میشود:
$$Q_ { water } = Q_ {person} \ m_{water} L_ V = m_{person} c_ { person } triangle theta \ m_ { water } times ( 2.42 times 10 ^ 6 frac { J } { kg } ) = 50.0 kg times 3480 frac { J } { kg . K } times (1.00 K ) $$
با حل معادله فوق، مقدار آب تبخیر شده در حدود ۷۲ گرم بهدست میآید.
قسمت ب: برای بهدست آوردن حجم آب از تعریف چگالی استفاده میکنیم:
$$rho = frac { m } { V } \ V = frac { m } { rho } = frac { 0.075 kg } { 1.00 times 10 ^ 3 frac { kg } { m^ 3 } } = 7.19 times 10 ^ { -5 } m^ 3$$
مسائل مربوط به انتقال گرما فصل چهارم ترمودینامیک فیزیک دهم
روشهای انتقال گرما یکی دیگر از بخشهای مهم ترمودینامیک فیزیک دهم است. در ادامه، سه مسئله در این مورد حل میکنیم.
مسئله ۲۴
اگر تیر چوبی و لوله فلزی سردی را که همدما هستند لمس کنید، چرا حس میکنید لوله سردتر است؟ چرا ممکن است دست شما به لوله بچسبد؟

پاسخ
دلیل آنکه لوله فلزی سردتر از تیر چوبی به نظر میرسد، به تفاوت رسانایی گرمایی آنها مربوط میشود. فلز رسانای خوبی برای انتقال گرما است. این بدان معنا است که گرما در فلزات به سرعت از نقطهای به نقطه دیگر منتقل میشود. بنابراین، لوله فلزی گرمای بدن شما را سریعتر از تیر چوبی دریافت و به نقطهای دیگر منتقل میکند. دست شما رطوبت دارد. این رطوبت به هنگام تماس با لوله فلزی به سرعت منجمد و با سطح فلز، پیوند تشکیل میدهد.
مسئله ۲۵
پالتو چگونه شما را گرم نگه میدارد؟ چرا استفاده از چند لباس زیر پالتو، این عمل را تشدید میکند؟
پاسخ
در بین الیاف پالتو هوا وجود دارد. از آنجا که هوا رسانای خوبی برای انتقال گرما نیست، گرمای بدن شما نمیتواند به محیط اطراف منتقل شود، بنابراین احساس سرما نخواهید کرد. پوشیدن چند لباس زیر پالتو سبب افزایش لایههای هوا و کاهش انتقال گرما میشود.

مسئله ۲۶
دو قوری همجنس و هماندازه را در نظر بگیرید که سطح بیرونی یکی سیاهرنگ و دیگری سفیدرنگ است. هر دو را با آبِ داغ با دمای یکسان پر میکنیم. آبِ کدام قوری زودتر خنک میشود؟
دو قوری همزمان خنک میشوند.
آبِ داخلی قوری سیاه سریعتر از آبِ داخل قوری سفید، خنک میشود.
آبِ داخلی قوری سفید سریعتر از آبِ داخل قوری سیاه، خنک میشود.
آبِ داخلی قوری سیاه سریعتر از آبِ داخل قوری سفید، خنک میشود. زیرا اجسام سیاهرنگ گرمای بیشتری را از محیط اطراف خود جذب و گرمای جذب شده را نیز با سرعت بیشتری به اطراف منتشر میکنند.

مسائل مربوط به قوانین گازها فصل چهارم ترمودینامیک فیزیک دهم
در پایان فصل چهارم از ترمودینامیک فیزیک دهم با قوانین گازها آشنا شدیم. در ادامه، برای درک بهتر این موضوع چند مسئله را با یکدیگر حل میکنیم.
مسئله ۲۷
گازی در دمای ۲۰ درجه سلسیوس دارای حجم ۱۰۰/۰ سانتیمتر مکعب است. الف) این گاز را باید تا چه دمایی گرم کنیم تا در فشار ثابت، حجم آن ۲۰۰/۰ سانتیمتر مکعب شود؟ ب) این گاز در همین فشار در چه دمایی دارای حجمِ ۵۰/۰ سانتیمتر مکعب خواهد شد؟
پاسخ
قسمت الف: در مسئله ۲۷ با فرایند همفشار روبرو هستیم. در این فرایند، حجم به صورت مستقیم با دما تغییر میکند و نسبت حجم به دما ثابت است:
$$frac { V } { T } = comstant \ frac { V _ 1 } { T _ 1 } = frac { V _ 2 } { T _ 2 } $$
مقدارهای داده شده را در رابطه فوق قرار میدهیم. به این نکته توجه داشته باشید که دما باید به کلوین تبدیل شود.
$$frac { 100 cm^ 3 } { 20 + 273 } = frac { 200 cm^ 3 } { T _ 2 } \ T_2 = 586 K = 313 ^ oC$$
قسمت ب: برای آنکه بدانیم گاز در چه دمایی به حجم ۵۰/۰ سانتیمتر مکعب میرسد، به صورت زیر عمل میکنیم:
$$frac { 100 cm^ 3 } { 20 + 273 } = frac { 50 cm^ 3 } { T _ 2 } \ T_2 = 146.5 K = -126.5 ^ oC$$
مسئله ۲۸
هوایی با فشار ۱/۰ اتمسفر درون استوانه تلمبه دوچرخهای به طول ۲۴ سانتیمتر محبوس است. راههای ورودی و خروجی هوا را میبندیم. اکنون:
الف) اگر طول استوانه را در دمای ثابت به ۳۰/۰ سانتیمتر افزایش دهیم، فشار هوای محبوس چقدر خواهد شد؟
ب) برای آنکه در دمای ثابت، فشار هوای محبوس ۳/۰ اتمسفر شود، طول استوانه را چقدر باید کاهش دهیم؟
الف: ۰/۸ اتمسفر، ب: ۸ سانتیمتر
الف: ۰/۲ اتمسفر، ب: ۱۶ سانتیمتر
الف: ۰/۸ اتمسفر، ب: ۱۰ سانتیمتر
الف: ۰/۸ اتمسفر، ب: ۱۶ سانتیمتر
در این مسئله دما ثابت است، بنابراین بر طبق قانون گازها از ترمودینامیک فیزیک دهم داریم:
$$P_1 V_ 1 = P_2 V_ 2$$
مساحت قاعده استوانه را برابر A در نظر میگیریم. حجم استوانه برابر حاصلضرب مساحت قاعده در ارتفاع است:
$$ ( 1 atm ) times ( 24 cm times A ) = P_ 2 times ( 30 cm times A) \ P _ 2 = 0.8 atm $$
در قسمت ب میخواهیم بدانیم طول استوانه چه مقدار باید کاهش یابد، تا فشار محبوس در داخل آن به مقدار ۳/۰ اتمسفر افزایش یابد:
$$ ( 1 atm ) times ( 24 cm times A ) = (3 atm ) times ( L cm times A) \ L = 8 cm $$
بنابراین، طول استوانه باید به اندازه ۱۶ سانتیمتر کاهش یابد.
مسئله ۲۹
لاستیک اتومبیلی حاوی مقدار معینی هوا است. در دمای ۱۷ درجه سلسیوس، فشارسنج، فشار درون لاستیک را ۲/۰۰ اتمسفر نشان میدهد. پس از رانندگی بسیار سریع، فشار هوای درون لاستیک دوباره اندازهگیری میشود و مقدار ۲/۳۰ اتمسفر بهدست میآید. دمای هوای درون لاستیک در این وضعیت چقدر است؟ حجم لاستیک را ثابت و فشار جو را ۱/۰۰ اتمسفر در نظر بگیرید.
۴۶ درجه سلسیوس
۳۶ درجه سلسیوس
۴۰ درجه سلسیوس
۶۶ درجه سلسیوس
در این مسئله از ترمودینامیک فیزیک دهم، حجم ثابت در نظر گرفته شده است:
$$frac { P _ 1 } { T_ 1 } = frac { P _2 } { T _ 2 } $$
با قرار دادن مقدارهای داده شده در رابطه فوق، دمای لاستیک را پس از رانندگی سریع بهدست میآوریم:
$$frac { P _ 1 } { T_ 1 } = frac { P _2 } { T _ 2 } \ frac { (2 atm + 1 atm) } { 273 + 17 } = frac { (2.3 atm + 1 atm ) } { T _ 2 } \ T_ 2 = 319 K \T_2 = 46 ^oC$$
به این نکته توجه داشته باشید که فشارسنج، فشار پیمانهای را نشان میدهد، اما در رابطه فوق باید فشار مطلق را قرار دهیم.
مسئله ۳۰
دما و فشار متعارف برای گاز، دمای ۲۷۳ کلوین و فشار $$1 atm = 1.013 times 10 ^ 5 Pa$$ معرفی میشود. حجم یک مول گاز کامل در دما و مفشار متعارف چقدر است؟
قانون گاز کامل در ترمودینامیک فیزیک دهم به صورت زیر نوشته میشود:
$$PV = n RT \ 1.013 times 10 ^ 5 Pa times V = ( 1 .00 mol) times ( 8.314 frac { J } { mol. K } times ( 273 K ) \ V = 0.0224 m ^ 3 = 22.4 L$$
مسئله ۳۱
حباب هوایی به حجم ۰/۲۰ سانتیمتر مکعب در ته دریاچهای به عمق ۴۰/۰ متر قرار دارد که دما در آنجا ۴/۰ درجه سلسیوس است. حباب تا سطح آب بالا میآید. دمای سطح آب برابر ۲۰ درجه سلسیوس است (دمای هوای حباب با دمای آبِ اطراف آن یکسان است). در لحظهای که حباب به سطح آب میرسد، حجم آن چه مقدار است؟ فشار هوا در سطح دریاچه برابر $$1.01 times 10 ^ 5$$ پاسکال در نظر گرفته میشود.

۱/۱۵ سانتیمتر مکعب
۱/۲۳ سانتیمتر مکعب
۱/۰۳ سانتیمتر مکعب
۰/۱۳ سانتیمتر مکعب
برای حل این مسئله از قانون گاز کامل در ترمودینامیک فیزیک دهم استفاده میکنیم:
$$PV = nRT \ frac { P_1 V_ 1 } { T _ 1 } = frac { P_2 T _ 2 } { T _ 2 }$$
حباب ابتدا در عمق ۴۰/۰ متری از سطح دریاچه قرار دارد. فشار وارد شده بر حباب در این عمق برابر است با:
$$P_1 = P_0 + rho g h = 1.01 times 10 ^ 5 + ( 1.0 times 10 ^ 3 frac { kg } { m ^ 3 } times 9.8 times 40.0 m ) = 4.92 times 10 ^ 5 Pa$$
فشارِ روی حباب پس از رسیدن به سطح دریاچه برابر فشار اتمسفر است. با قرار دادن مقدارهای بهدست آمده و داده شده در رابطه $$V_ 2 = frac { T _ 2 } { T _1 } times { P _1 } { P _ 2 } $$، حجم حباب در سطح دریاچه برابر ۱/۰۳ سانتیمتر مکعب بهدست میآید.
تا اینجا با مفاهیم گرما، دما، ظرفیت گرمایی و روشهای انتقال گرما از فصل چهارم ترمودینامیک فیزیک دهم آشنا شدیم. توجه به این نکته مهم است که فیزیک رشته تجربی در این فصل به پایان میرسد، اما ترمودینامیک فیزیک دهم در رشته ریاضی در فصل پنجم نیز ادامه مییابد.
فصل پنجم ترمودینامیک فیزیک دهم
در این فصل مباحثی مانند تبادل انرژی و قوانین اول و دوم ترمودینامیک مطرح میشوند. در ادامه، به اختصار در مورد این مفاهیم صحبت و در پایان مسائل فصل پنجم ترمودینامیک فیزیک دهم را با یکدیگر حل میکنیم.
ترمودینامیک چیست؟
ترمودینامیک شاخهای از علم فیزیک است که در مورد گرما، کار، دما و رابطه آنها با انرژی، تشعشع و ویژگیهای فیزیکی ماده مطالعه میکند. این کلمه از دو بخش ترمو به معنای گرما و دینامیک به معنای انتقال گرما یا انرژی، تشکیل شده است. از اینرو، در ترمودینامیک در مورد رابطه بین چگونگی انتقال گرما یا انرژی از نقطهای به نقطه دیگر صحبت میکنیم. قبل از صحبت در مورد قانونهای ترمودینامیک، ابتدا کمی در مورد انواع سیستمها و برخی مفاهیم مهم در ترمودینامیک صحبت میکنیم.
تعریف سیستم در ترمودینامیک چیست؟
به قسمتی از جهان است که ویژگیهای ترمودینامیکی آن برای ما جالب است، سیستم ترمودینامیکی گفته میشود. سیستمهای ترمودینامیکی به سه دسته تقسیم میشوند:
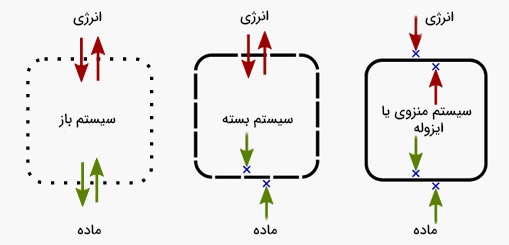
- سیستم باز: در سیستم باز، جرم یا در حالت کلی ماده میتواند به داخل یا خارج سیستم جریان داشته باشد. به عنوان مثال، در ظرف پر شده از آب و بدون درپوش، اکسیژن به راحتی میتواند به وارد سیستم یا از آن خارج شود.
- سیستم بسته: در این حالت، سیستم مهروموم شده است. بنابراین، ماده یا جرم نمیتواند به سیستم وارد یا از آن خارج شود. به عنوان مثال، گاز اکسیژن در هوا وارد سیستم بسته ترمودینامیکی نخواهد شد. اما، انرژی گرمایی میتواند به سیستم بسته ترمودینامیکی وارد یا از آن خارج شود. از اینرو، سیستم بسته ترمودینامیکی در مقابل گرما ایزوله نیست.
- سیستم ایزوله یا منزوی: در این حالت، سیستم ترمودینامیکی به خوبی ایزوله شده است. در سیستم ایزوله همانند سیستم بسته، ماده نمیتواند به سیستم وارد یا از آن خارج شود. علاوه بر ماده، در سیستمهای ایزوله ترمودینامیکی، گرما نیز نمیتواند به سیستم وارد یا از آن خارج شود.
متغیر ترمودینامیکی چیست؟
سیستم ترمودینامیکی با استفاده از کمیتهایی به نام متغیر تعریف و مطالعه میشود. برخی از این کمیتها، مانند فشار و دما را میتوانیم به راحتی اندازه بگیریم. متغیرها تنها به حالت کنونی سیستم بستگی دارند و آن را تعریف میکنند. با دانستن تمام متغیرهای مرتبط با سیستم میتوانیم حالت سیستم را بهدست آوریم. دما، فشار و حجم مهمترین متغیرهای ترمودینامیکی هستند. با تعریف دما در مطالب بالا آشنا شدیم.
فشار چیست؟
فشار در فیزیک به صورت نسبت نیروی اعمال شده بر جسم بر مساحت سطح تماس، تعریف و رابطه آن به صورت $$frac { F} { A}$$ نوشته میشود. پاسکال، واحد اصلی فشار در سیستم SI است.
حجم چیست؟
هر جسم سهبعدی مقدار مشخصی از فضا را اشغال میکند. به مقدار فضای اشغال شده توسط جسم۷ حجم میگوییم.
تعادل ترمودینامیکی چیست؟
حالت تعادل در ترمودینامیک فیزیک دهم به حالتی گفته میشود که تمام نیروهای وارد شده بر سیستم ناپدید شدهاند و سیستم همانگونه که بود، باقی میماند و با گذر زمان تغییری در آن ایجاد نمیشود. سیستم متعادل، حالت کنونی خود را همانگونه که است نگه میدارد، زیرا هیچ نیروی خارجی بر آن وارد نمیشود. دو جسم با دمای یکسان در تعادل گرمایی قرار دارند. در این حالت، انرژی گرمایی بین دو جسم مبادله نخواهد شد. تعادل مکانیکی هنگامی رخ میدهد که دو ماده فشار یکسانی داشته باشند. برای آنکه سیستمی در تعادل ترمودینامیکی قرار داشته باشد باید تمام متغیرهای ترمودینامیکی آن مانند فشار، حجم و دما، ثابت باشند. در نتیجه، تغییرات کلی هر یک از این متغیرهای در حالت تعادل برابر صفر خواهد بود.

اگر سیستم در تعادل ترمودینامیکی باشد، حالتهای ماکروسکوپی تغییر نمیکنند. در زمان صفر، حالتهای میکروسکوپی اتمهای مختلف را داریم. پس از گذشت مدت زمانی مشخص، حالتهای میکروسکوپی به طور کامل تغییر میکنند، زیرا ذرات داخل سیستم به طور پیوسته به یکدیگر برخورد میکنند و تکانه یا انرژی خود را به ذرات مجاور منتقل میکنند. گرچه سیستم در حالت تعادل ترمودینامیکی قرار دارد و حالت ماکروسکوپی آن ثابت است، حالتهای میکروسکوپی در بازههای زمانی بسیار کوتاه، به سرعت تغییر میکنند. بنابراین، در ترمودینامیک تمایل داریم از حالتهای ماکروسکوپی به جای میکروسکوپی استفاده کنیم.
معادله حالت چیست؟
معادله حالت در ترمودینامیک فیزیک دهم عبارتی ریاضی است که حالت ترمودینامیکی سیستم را برحسب متغیرهای ترمودینامیکی توصیف میکند. به بیان دیگر، متغیرهای ترمودینامیکی توسط معادله حالت به یکدیگر مربوط میشوند. قانون گاز ایدهال یکی از آشناترین مثالهای معادله حالت در ترمودینامیک است و به صورت زیر نوشته میشود:
$$PV = n R T$$
طرفین رابطه فوق را بر n، تعداد مولها، تقسیم میکنیم:
$$P frac { V } { n } = RT \ P overline { V } = RT$$
در رابطه فوق، P فشار سیستم، $$overline { V } $$ حجم مولی و R ثابت جهانی گازها است.
فرایند ترمودینامیکی چیست؟
فرایند ترمودینامیکی در فصل پنجم ترمودینامیک فیزیک دهم از اهمیت بالایی برخوردار است. سیستمی ترمودینامیکی را از حالت اولیه تا حالت نهایی آن در نظر بگیرید. این سیستم برای رفتن از حالت اولیه به حالت نهایی باید مسیرهای مختلفی را طی کند. سیستمی مشخص هنگامی تحت فرایند ترمودینامیکی قرار میگیرد که در آن مقداری تغییر انرژی وجود داشته باشد. این تغییر انرژی با تغییرات فشار، حجم و انرژی درونی همراه است. قبل از توضیح در مورد انواع فرایندهای ترمودینامیکی، فرایندی به نام «فرایند ایستاوار» (Quasi-static Process) را تعریف میکنیم. اگر در فرایندی، سیستم در هر لحظه با محیط اطرافش در تعادل ترمودینامیکی باشد، به آن فرایند ایستاوار گفته میشود. گفتیم در فرایند ترمودینامیکی، مقداری تغییر انرژی در سیستم رخ میدهد.
تغییر انرژی به دلیل تبادل انرژی بین سیستم و محیط اطراف آن رخ میدهد. تبادل انرژی بین سیستم و محیط اطراف از دو طریق گرما و کار انجام میشود. به طور معمول، سیستم موردمطالعه را در تماس با منبع گرما در نظر میگیریم. منبع گرمایی ویژگی بسیار مهمی دارد، دمای آن به هنگام تماس با سیستمهای مختلف، هیچ تغییری نمیکند. در واقع، جرم منبع گرمایی در مقایسه با جرم سیستمِ در تماس با آن به اندازهای بزرگ است که حتی با دریافت یا از دست دادن مقدار زیادی گرما، باز هم تغییر محسوسی در دمای آن مشاهده نمیشود. به عنوان مثال، لیوانی چای داغ را داخل اتاقی بزرگ در نظر بگیرید.
دمای چای پس از گذشت مدت زمانی مشخص کاهش مییابد و گرما از چای با دمای بالاتر به هوای اتاق با دمای کمتر منتقل میشود. آیا دمای اتاق افزایش مییابد؟ خیر، در این حالت اتاق همانند منبع گرما عمل میکند و تغییر محسوسی در دمای آن احساس نمیشود. تاکنون با برخی از مهمترین مفاهیم در ترمودینامیک آشنا شدیم. در ادامه، در مورد قوانین ترمودینامیک و انواع فرایندهای ترمودینامیکیِ مطرح شده در ترمودینامیک فیزیک دهم صحبت میکنیم.
قوانین ترمودینامیک چیست؟
ترمودینامیک از چهار قانون تشکیل شده است:
قانون صفرم ترمودینامیک
بر طبق قانون صفرم قوانین ترمودینامیک، اگر دو سیستم به نامهای A و B با سیستم سومی به نام C در تعادل ترمودینامیکی باشند، سیستمهای A و B نیز در تعادل ترمودینامیکی با یکدیگر خواهند بود. به بیان دیگر، اگر سیستم A در تعادل ترمودینامیکی با سیستم C و سیستم B نیز در تعادل ترمودینامیکی با سیستم C باشد، سیستمهای A و B نیز در تعادل ترمودینامیکی با یکدیگر قرار دارند.
قانون اول ترمودینامیک
قانون اول ترمودینامیک در ترمودینامیک فیزیک دهم با انرژی درونی، گرما و کار ارتباط دارد. ایده بنیادی قانون اول ترمودینامیک چیست؟ این قانون، بیان دیگری از اصل پایستگی انرژی است. بر طبق این اصل، انرژی نه به وجود میآید، نه از بین میرود، بلکه از حالتی به حالت دیگر تبدیل یا از مکانی به مکان دیگر منتقل میشود. سیستم دلخواهی را به صورت نشان داده شده در تصویر زیر در نظر بگیرید.
همانطور که در بخش قبل اشاره شد انرژی از دو طریق کار و گرما میتواند به سیستم وارد یا از آن خارج شود. سیستمی را در نظر بگیرید که مقدار مشخصی انرژی به آن وارد میشود. در این حالت، سیستم انرژی بهدست میآورد. به این انرژی، انرژی درونی سیستم میگوییم و آن را با U نشان میدهیم. محیط اطراف نیز میتواند روی سیستم کار انجام دهد. از اینرو انرژی درونی سیستم میتواند از دو طریق انتقال گرما به سیستم یا انجام کار روی آن افزایش یابد. فرض کنید محیط اطراف، ۱۵۰ ژول کار روی سیستم انجام میدهد. بنابراین، انرژی داخلی سیستم به اندازه ۱۵۰ ژول افزایش مییابد. از اینرو، تغییرات انرژی درونی سیستم مثبت خواهد بود:
$$triangle U = + 150 J$$
در این حالت، محیط اطراف سیستم انرژی برابر ۱۵۰ ژول از دست میدهد. بنابراین، انرژی نه به وجود آمد، نه از بین رفت، بلکه از محیط اطراف به سیستم منتقل شد. سیستم نمیتواند خودبهخود انرژی به اندازه ۱۵۰ ژول تولید کند و انرژی داخلی خود را افزایش دهد. این انرژی باید از جای دیگری به آن منتقل شده باشد. اگر سیستم انرژی برابر ۳۰۰ ژول از دست بدهد، انرژی درونی آن به همین اندازه کاهش مییابد. در مقابل، این مقدار انرژی به محیط اطراف سیستم منتقل میشود و انرژی درونی آن ۵۰۰ ژول افزایش مییابد. از این رو، قانون اول ترمودینامیک بیان دیگری از قانون بقای انرژی است.
تغییرات انرژی درونی سیستم را میتوانیم با استفاده از رابطه زیر بهدست آوریم:
$$triangle U = Q + W$$
به هنگام حل مسائل مربوط به تغییر انرژی درونی سیستم باید به نکتههای زیر توجه داشته باشیم:
- کار انجام شده توسط سیستم روی محیط، منفی در نظر گرفته میشود. سیستم برای انجام کار باید انرژی مصرف کند. بنابراین، انرژی درونی آن کاهش مییابد.
- در مقابل، کار انجام شده روی سیستم توسط محیط اطراف آن، مثبت در نظر گرفته میشود.
- اگر گرما به سیستم وارد شود، گرما را مثبت و اگر گرما از سیستم خارج شود، آن را منفی در نظر میگیریم.
مثال قانون اول ترمودینامیک
۱) فرض کنید مقدار گرمایی برابر ۴۰ ژول به سیستمی وارد میشود. همزمان سیستم مقدار کاری برابر ۱۰ ژول را انجام میدهد. در ادامه، ۲۵ ژول گرما از سیستم خارج و ۴ ژول کار روی سیستم انجام میشود. تغییرات انرژی داخلی سیستم را بهدست آورید.
۲) اگر مقدار گرمایی برابر ۱۵۰ ژول از سیستم خارج و مقدار کاری برابر ۱۵۹ ژول روی آن انجام شود، تغییرات انرژی درونی سیستم چه مقدار خواهد بود؟

پاسخ
برای پاسخ به قسمت یک، ابتدا باید مقدار کلِ گرمای منتقل شده و مقدار کلِ کار انجام شده را بهدست آوریم. بر طبق قانون اول ترمودینامیک تغییرات انرژی درونی سیستم با استفاده از رابطه زیر بهدست میآید:
$$triangle U = Q + W$$
قسمت ۱
همانطور که گفتیم برای حل مسائل مربوط به قانون اول ترمودینامیک اگر گرما به سیستم وارد شود، گرما را مثبت و اگر گرما از سیستم خارج شود، آن را منفی در نظر میگیریم. از اینرو، ۴۰ ژول گرمای وارد شده به سیستم را مثبت و ۲۵ ژول گرمای خارج شده از سیستم را منفی در نظر میگیریم.
$$Q = 40 J – 25 J = 15 J$$
همچنین، کار انجام شده توسط سیستم روی محیط، منفی در نظر گرفته میشود.در مقابل، کار انجام شده روی سیستم توسط محیط اطراف آن، مثبت در نظر گرفته میشود. در قسمت یک سیستم ابتدا ۱۰ ژول کار روی محیط انجام میدهد. در این حالت، مقدار کار برابر ۱۰- ژول است. در ادامه، محیط، ۴ ژول کار روی سیستم انجام میدهد. در نتیجه، مقدار کار برابر ۴+ ژول خواهد بود. از اینرو، مقدار کل کار انجام شده برابر است با:
$$W = -10 J + 4 J = -6 J$$
تغییرات انرژی درونی سیستم در قسمت یک برابر است با:
$$triangle U = Q + W \ triangle U = 15 J – 6 J = 9 J$$
تغییرات انرژی درونی سیستم در قسمت یک را میتوانیم با محاسبه تغییرات انرژی درونی هر مرحله و جمع جبری آنها با یکدیگر نیز بهدست آوریم.
$$triangle U _1 = Q_1 + W_1 = 40 J – 10 J = 30 J \ triangle U_2 = O_2 + W_2 = -25 J + 4 J = -21 J \ triangle U = triangle U_1 + triangle U _ 2 = 30 J – 21 J = 9 J$$
قسمت ۲
در قسمت ۲ مقدار گرمایی برابر ۱۵۰ ژول از سیستم خارج میشود، بنابراین علامت آن منفی است. همچنین، کاری برابر ۱۵۹ ژول روی سیستم انجام میشود. کار انجام شده توسط محیط روی سیستم را مثبت در نظر میگیریم. از اینرو، تغییرات انرژی داخلی برابر است با:
$$triangle U = Q + W = -150 J + 159 J = 9 J$$
انواع فرایندهای ترمودینامیکی
فرایندهای ترمودینامیکی در ترمودینامیک فیزیک دهم به چهار دسته تقسیم میشوند. هر دسته ویژگیهای منحصر به خود را دارد.
فرایند هم حجم
در این فرایند، تغییر حجم سیستم و در نتیجه کار انجام شده برابر صفر خواهد بود. ثابت ماندن حجم به معنای برابر بودن حجم سیستم در آغاز و پایان فرایند است.
$$V _ f = V _ i (triangle V = 0 , d V = 0 )$$
از آنجا که کار انجام شده توسط سیستم در این فرایند برابر صفر است، تغییرات گرما برابر تغییرات انرژی درونی سیستم است:
$$triangle U = Q$$
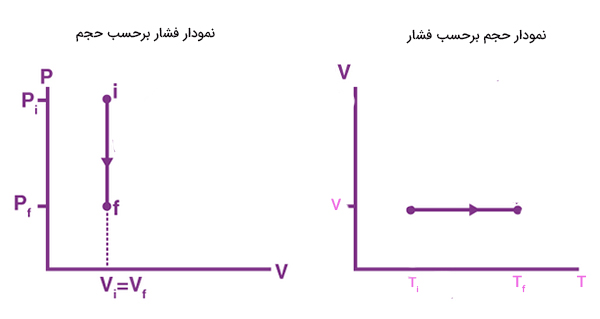
«چرخه اتو ایدهال» (Ideal Otto Cycle) مثال خوبی برای فرایند همحجم است. هنگامیکه مخلوط هوا و گازوئیل در موتور اتومبیل میسوزند، دما و فشار گاز داخل موتور افزایش مییابد، اما حجم گاز بدون تغییر باقی خواهد ماند. فرایند همحجم در نمودارهای فشار برحسب حجم و حجم برحسب دما به صورت زیر نشان داده میشود:
فرایند هم فشار یا ایزوبار
فرایند همفشار، فرایندی ترمودینامیکی است که در فشار ثابت رخ میدهد. نام «ایزوبار» (Isobar) از کلمههای یونانی Iso به معنای مساوی و baros به معنای فشار گرفته شده است. فشار ثابت هنگامی بهدست میآید که حجم منبسط یا منقبض میشود. به این ترتیب، هر تغییر فشاری به دلیل انتقال گرما، خنثی خواهد شد. در فرایند همفشار، به هنگام انتقال گرما به سیستم، مقداری کار انجام میشود. نباید فراموش کنیم علاوه بر انجام کار، انرژی درونی سیستم نیز تغییر میکند. این بدان معنا است که هیچ کمیتی در قانون اول ترمودینامیک برابر صفر نمیشود.
$$P_ i = P _f enspace ( triangle P = 0 )$$
در تصویر زیر حالتی را مشاهده میکنید که در آن حالت گاز با ثابت نگه داشتن فشار، تغییر میکند.
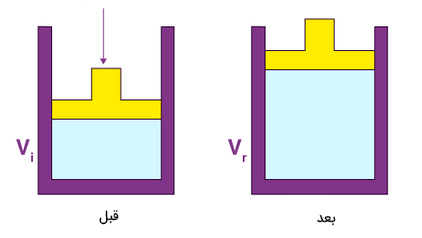
گازی درون استوانهای به صورت نشان داده شده در تصویر بالا با پیستون متحرک و بدون جرمی قرار گرفته است. پیستون میتواند در راستای عمودی به سمت بالا یا پایین حرکت کند، اما استوانه به گونهای ساخته شده است که هیچ اتمی نمیتواند به محیط داخلی استوانه وارد یا از آن خارج شود. جرمی به جرم M روی پیستون قرار میگیرد. این جرم نیروی ثابتی برابر Mg به سمت پایین بر پیستون وارد میکند. همچنین، فشاری برابر $$P_ { atm }$$ نیز از طرف اتمسفر بر پیستون وارد میشود. به این نکته توجه داشته باشید که در حالت تعادل فشاری به سمت بالا، $$P$$، از طرف گاز بر پیستون وارد میشود. در حالت تعادل، فشار وارد شده از سمت گاز بر پیستون با مجموع فشار اتمسفر و فشار وارد شده از طرف جرم بر پیستون با یکدیگر برابر هستند:
$$P = P_ { atm } + frac { Mg } { A }$$
در رابطه فوق:
- $$P_{ atm }$$ فشار اتمسفر است.
- A سطح مقطع پیستون و M جرم جسم قرار داده شده روی پیستون هستند.
- P فشار گاز است.
همانطور که در رابطه فوق مشاهده میکنید، فشار گاز مستقل از دمای گاز یا ارتفاع پیستون است. از اینرو، مقدا آن تا زمانی که جرم قرار داده شده روی پیستون تغییر نکند، ثابت باقی میماند. اگر استوانه در تماس با منبع گرمایی قرار بگیرد، گاز منبسط میشود و پیستون به سمت بالا حرکت میدهد. از آنجا که فشار گاز تنها به جرم قرار گرفته روی پیستون بستگی دارد، تا هنگامیکه M ثابت است، مقدار فشار نیز تغییر نخواهد کرد. این فرایند به صورت فرایند فشار ثابت روی نمودار PV نشان داده شده است.
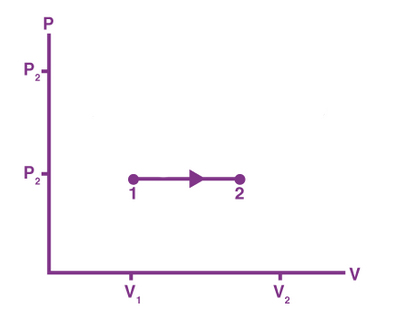
کار انجام شده در فرایند همفشار با استفاده از رابطه زیر بهدست میآید:
$$W = – P_ i (triangle V )$$
اگر گاز منبسط شود، حجم نهایی بزرگتر از حجم اولیه و کار انجام شده توسط گاز منفی است. اگر گاز فشرده شود، حجم نهایی کوچکتر از حجم اولیه و کار انجام شده توسط گاز مثبت خواهد بود.
فرایند هم دما
فرایند همدما، فرایندی ترمودینامیکی است که در دمای ثابت رخ میدهد. به بیان دیگر، دمای سیستم در فرایند همدما ثابت میماند. در واقع، انتقال گرما به سیستم یا خروج گرما از آن به اندازهای آهسته انجام میشود که تعادل گرمایی برقرار باشد. این فرایند میتواند هنگامی رخ دهد که سیستم با منبع گرمایی خارجی در تماس باشد. در این حالت برای برقرار تعادل، سیستم به آهستگی و با استفاده از تبادل حرارتی، دمای خود را با دمای منبع خارجی تطبیق میدهد. از آنجا که انرژی درونی گاز ایدهال، تنها به دما وابسته و در فرایند همدما، دمای سیستم بدون تغییر باقی میماند، تغییر انرژی درونی برابر صفر خواهد بود:
$$triangle U = 0 \ triangle U = Q + W = 0 \ Q = – W$$
نکته: در تراکم یا انبساط گاز، کار انجام شده توسط محیط روی گاز، مثبت است، بنابراین Q منفی خواهد شد.
مثال فرایند همدما
نمودار فشار برحسب حجم دو فرایند همدما در دو دمای متفاوت در تصویر زیر نشان داده شده است. دمای کدام فرایند بیشتر است؟
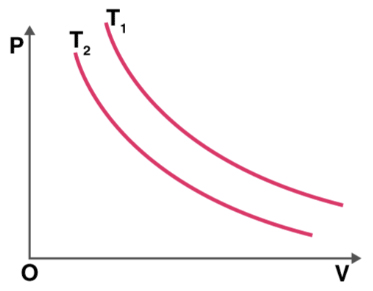
پاسخ
برای آنکه بدانیم دمای کدام فرایند بالاتر است، به صورت زیر عمل میکنیم:
- ابتدا، خطی افقی و موازی محور حجم رسم میکنیم.
- خط افقی، خط فشار ثابت را نشان میدهد.
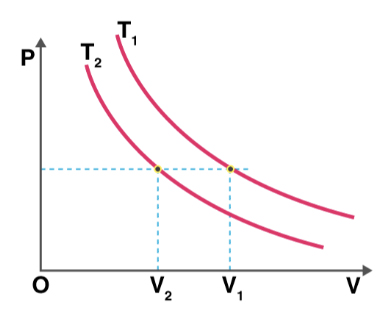
- فرض کنید $$V _ 1$$ و $$V_ 2$$ به ترتیب حجمهای متعلق به دماهای $$T_ 2 $$ و $$T_1$$ هستند.
- میدانیم در فشار ثابت، با افزایش حجم گاز، دما نیز افزایش مییابد.
- با توجه به نمودار نشان داده شده در تصویر زیر میتوان گفت حجم $$V _ 1$$ بزرگتر از حجم $$V _ 2$$ است. بنابراین، دمای $$T_1$$ نیز بزرگتر از دمای $$T_2$$ خواهد بود.
- راه آسانتر دیگری نیز برای تعیین دما وجود دارد. نموداری که به مبدأ نزدیکتر است، دمای پایینتری خواهد داشت.
فرایند بی درو یا آدیاباتیک
در این فرایند، هیچ گرمایی به سیستم وارد یا از آن خارج نمیشود. توجه به این نکته مهم است که در فرایند بیدررو، تبادل گرمایی به هنگام انبساط یا انقباض سیستم، برابر صفر خواهد بود. این فرایند میتواند برگشتپذیر یا برگشتناپذیر باشد. شرایط زیر برای رخ دادن این فرایند ضروری هستند:
- سیستم باید به طور کامل از محیط اطراف خود جدا شده باشد.
- فرایند باید سریع انجام شود تا زمان کافی برای انتقال گرما وجود نداشته باشد.
به عنوان مثال، تراکم گاز داخل سیلندر موتور به اندازهای سریع رخ میدهد که در مدت زمان تراکم، مقدار انرژی تولید شده داخل سیستم کمینه باشد. از آنجا که در فرایند بیدررو هیچ گرمایی از سیستم خارج یا به آن وارد نمیشود، Q برابر صفر خواهد بود:
$$triangle U = W$$
نکته: اگر گاز ایدهال به صورت بیدررو منبسط شود، کار محیط روی سیستم (گاز) منفی است. از اینرو، تغییرات انرژی درونی گاز منفی است و دمای آن کاهش مییابد. در مقابل، اگر گاز ایدهال به صورت بیدررو متراکم یا منقبض شود، تغییرات انرژی درونی آن مثبت است و دمای گاز افزایش خواهد یافت.
تا اینجا، میدانیم فرایندهای ترمودینامیکی و انواع آن در ترمودینامیک فیزیک دهم چیست. در فرایندهای ترمودینامیکی گفته شده ممکن است یکی از کمیتهای ترمودینامیکی دما، فشار یا حجم ثابت باقی بماند و دو فرایند دیگر تغییر کنند. در هر یک از فرایندهای گفته شده، حالت نهایی سیستم با حالت اولیه آن متفاوت است. آیا ممکن است حالتهای نهایی و اولیه سیستم با یکدیگر برابر باشند؟ بله. این حالت در فرایند چرخهای رخ میدهد.
فرایند چرخه ای در ترمودینامیک چیست؟
در فرایندهای چرخهای، حالت اولیه سیستم با حالت نهایی آن برابر است. همانطور که میدانیم تغییرات انرژی درونی سیستم همان تابع حالت است. بنابراین، در این حالت تغییرات انرژی درونی، یعنی $$triangle U$$ برابر صفر خواهد بود. در نتیجه، بر طبق قانون اول ترمودینامیک داریم:
$$triangle U = Q + W = 0 \ Q = – W$$
نکته: اندازه کار انجام شده در چرخه ترمودینامیکی برابر با مساحت سطح داخل چرخه در نمودار فشار برحسب حجم است. در چرخههای ساعتگرد، کار انجام شده روی سیستم، منفی و در چرخههای پادساعتگرد، کار انجام شده روس سیستم، مثبت است.
ماشین های گرمایی
یکی از مباحث مهم در ترمودینامیک فیزیک دهم، مبحث ماشینهای گرمایی است. امروزه، انسان بیشتر انرژی موردنیاز خود را از طریق ماشینهای گرمایی تامین میکند. این ماشینها با استفاده از برخی فرایندهای ترمودینامیکی میتوانند گرمای بهدست آمده از سوخت را به کار تبدیل کنند. در حالت کلی، ماشینهای گرمایی به دو دسته کلی تقسیم میشوند:
- ماشینهای برونسوز مانند ماشین بخار
- ماشینهای درونسوز مانند موتور خودروها

بازده ماشین گرمایی
دیدگاه ایدهال در هر ماشین گرمایی آن است که انرژی ورودی له آن تا حد امکان به انرژی مفید یا کار تبدیل شود. بازده هر ماشین گرمایی به صورت نسبت انرژی مفید خروجی به انرژی داده شده به ماشین تعریف میشود:
$$eta = frac { Useful enspace output enspace energy } {Input enspace energy }$$
انرژی ورودی به ماشین گرمایی همان گرمای داده شده به ماشین، $$Q_H$$، و انرژی مفید خروجی، همان کار انجام شده توسط ماشین است:
$$eta = frac { | W | } { Q_H }$$
قانون دوم ترمودینامیک به بیان ماشین گرمایی
قانون دوم ترمودینامیک به بیان ماشین گرمایی آخرین مبحث در ترمودینامیک فیزیک دهم است. تقریبا همه ماشینهای گرمایی با دو منبع گرمایی با دو دمای متفاوت کار میکنند. منبع گرمایی با دمای بالاتر با $$Q_H$$ و منبع گرمایی با دمای پایینتر با $$Q_L$$ نشان داده میشوند. مقداری از گرمای گرفته شده از منبع $$Q_H$$ به کار تبدیل و مابقی آن به منبع گرمایی با دمای پایینتر داده میشود. آیا ماشینهای گرمایی میتوانند تمام گرمای دریافتی از منبع گرمایی $$Q_H$$ را به کار تبدیل کنند؟ خیر. بر طبق قانون دوم ترمودینامیک، هیچ ماشین گرمایی نمیتواند پس از طی کردن چرخهای ترمودینامیکی، تمام گرمای دریافتی از منبع $$Q_H$$ را به کار تبدیل کند. به بیان دیگر، بازده هیچ ماشین گرمایی برابر ۱۰۰ درصد نیست.
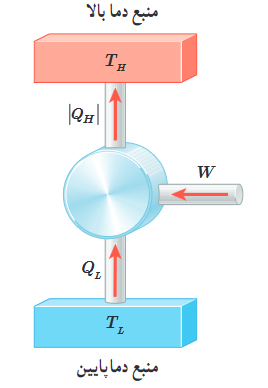
قانون دوم ترمودینامیک و یخچال ها
همانطور در فصل چهارم از ترمودینامیک فیزیک دهم دیدم، گرما از جسمی با دمای بالاتر به جسمی با دمای کمتر منتقل میشود. بنابراین، گرما نمیتوان به صورت خودبهخودی از جسم سرد به جسم گرم منتقل شود. این عبارت بیان یخچالی قانون دوم ترمودینامیک نام دارد. با انجام کار میتوان گرما را از جسمی با دمای پایینتر به جسمی با دمای بالاتر منتقل کرد. این کار توسط وسیلهای به نام یخچال انجام میشود. یخچال نیز همانند ماشین گرمایی چرخهای ترمودینامیکی را طی میکند. طرز کار یخچال ایدهال در تصویر زیر نشان داده شده است. همانطور که مشاهده میکنید، عملکرد ماشین گرمایی و یخچال معکوس یکدیگر هستند.
تا اینجا، با فصل پنجم از ترمودینامیک فیزیک دهم آشنا شدیم. برای درک بهتر مفاهیم مطرح شده در این بخش، چند مسئله از فصل پنجمِ ترمودینامیک فیزیک دهم را در ادامه با یکدیگر حل میکنیم.
حل مسائل فصل پنجم ترمودینامیک فیزیک دهم
در این بخش، مسائل فصل پنجم ترمودینامیک فیزیک دهم را با یکدیگر حل میکنیم.
مسئله ۱ فصل پنجم ترمودینامیک فیزیک دهم
ظرفی شامل ۳/۰ کیلوگرم آب است. با هم زدن آب داخل ظرف، ۴۰ کیلوژول کار روی آن انجام میدهیم و در این مدت ۳۱ کیلوژول گرما از ظرف به بیرون منتقل میشود. انرژی درونی آب چقدر تغییر میکند؟

پاسخ
همانطور که در بخشهای قبل اشاره شد، به هنگام حل مسائل مربوط به تغییر انرژی درونی سیستم باید به نکتههای زیر توجه داشته باشیم:
- کار انجام شده توسط سیستم روی محیط، منفی در نظر گرفته میشود. سیستم برای انجام کار باید انرژی مصرف کند. بنابراین، انرژی درونی آن کاهش مییابد.
- در مقابل، کار انجام شده روی سیستم توسط محیط اطراف آن، مثبت در نظر گرفته میشود.
- اگر گرما به سیستم وارد شود، گرما را مثبت و اگر گرما از سیستم خارج شود، آن را منفی در نظر میگیریم.
در این مسئله ظرف و آب درون آن را به عنوان سیستم انتخاب میکنیم. با هم زدن آب، ۴۰ کیلوژول کار روی آن انجام میدهیم. از آنجا که کار توسط محیط روی سیستم انجام شده است، علامت آن را مثبت در نظر میگیریم. همچنین، به هنگام هم زدن آب، ۳۱ کیلوژول گرما از ظرف به بیرون منتقل میشود. با توجه به آنکه سیستم گرما از دست داده است، علامت Q را منفی در نظر میگیریم. تغییر انرژی درونی آب برابر است با:
$$triangle U = Q + W = – 31 k J + 40 kJ = + 9 k J $$
مسئله ۲ فصل پنجم ترمودینامیک فیزیک دهم قسمت الف
در فرایند همحجم چگونه میتوان فشار گاز را افزایش داد؟
کار انجام شده در فرایند همحجم برابر صفر است. این بدان معنا است که سیستم هیچ کاری روی محیط اطراف انجام نمیدهد و گرمای اضافه شده به سیستم یا دریافت شده از آن، انرژی داخلی سیستم را تغییر خواهد داد. برای افزایش فشار در فرایند همحجم، باید دمای سیستم را با اضافه کردن گرما به آن، افزایش دهیم. برعکس، برای کاهش فشارِ سیستم باید دمای آن را با گرفتن گرما، کاهش دهیم.
مسئله ۲ فصل پنجم ترمودینامیک فیزیک دهم قسمت ب
در فرایند همفشار چگونه میتوان حجم گاز را افزایش یا کاهش داد؟
حجم گاز در فرایند همفشار با افزایش دما یا افزایش مقدار گاز در سیستم افزایش مییابد. همچنین، حجم گاز را میتوانیم با کاهش دما یا خروج گاز از سیستم، کاهش دهیم.
حجم گاز در فرایند همفشار با کاهش دما یا افزایش مقدار گاز در سیستم افزایش مییابد. همچنین، حجم گاز را میتوانیم با افزایش دما یا خروج گاز از سیستم، کاهش دهیم.
حجم گاز در فرایند همفشار با افزایش دما یا کاهش مقدار گاز در سیستم افزایش مییابد. همچنین، حجم گاز را میتوانیم با کاهش دما یا ورود گاز به سیستم، کاهش دهیم.
در فرایند همفشار، حجم میتواند با تغییر دما یا مقدار گازِ درون سیستم، تغییر کند:
- حجم گاز در فرایند همفشار را میتوان به دو روش افزایش داد:
- افزایش دما
- اضافه کردن گاز به سیستم
- حجم گاز در فرایند همفشار را میتوان به دو روش کاهش داد:
- کاهش دما
- خروج گاز از سیستم
مسئله ۳ فصل پنجم ترمودینامیک فیزیک دهم
ته سرنگی را که دسته آن میتواند آزادانه حرکت کند مسدود میکنیم، آن را درون مقداری آب میاندازیم و آب را به تدریج گرم میکنیم. هوای درون سرنگ چه فرایندی را طی میکند؟
فرایند همحجم
فرایند انبساط همفشار
فرایند همدما
هوای داخل سرنگ فرایند انبساط همفشار را طی میکند. در این حالت، فشار هوای داخل سرنگ، برابر فشار اتمسفرِ بیرون از سرنگ است. با افزایش دمای آب و هوای داخلِ سرنگ، مولکولهای هوا سریعتر حرکت میکنند و منبسط میشوند. از آنجا که انتهای سرنگ میتواند آزادانه حرکت کند، حجم هوا با ثابت ماندن فشار، افزایش مییابد.
مسئله ۴ فصل پنجم ترمودینامیک فیزیک دهم
نمودار P-V گازی رقیق در تصویر زیر نشان داده شده است. در این فرایند با فرض آنکه انرژی درونی در نقطه (۱) برابر ۴۵۶ ژول و در نقطه (۲) برابر ۹۱۲ ژول باشد، چقدر گرما مبادله شده است؟ آیا گاز گرما گرفته یا گرما از دست داده است؟
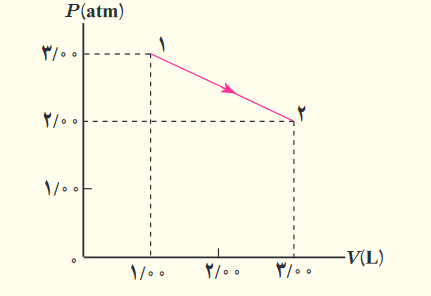
۹۵۶ ژول، گاز گرما از دست داده است.
۸۵۶ ژول، گاز گرما از دست داده است.
۸۵۶ ژول، گاز گرما گرفته است.
۹۵۶ ژول، گاز گرما گرفته است.
انرژی درونی گاز در ابتدا و انتهای فرایند داده شده است. بنابراین تغییرات انرژی درونی فرایند برابر است با:
$$triangle U = U_2 – U_1 = 912 J – 456 J = 456 J$$
بر طبق قانون اول ترمودینامیک، تغییرات انرژی درونی سیستم برابر است با:
$$triangle U = Q + W$$
برای محاسبه گرمای مبادله شده، باید مقدار کار انجام شده در این فرایند را محاسبه کنیم. قدر مطلق کار انجام شده برابر مساحت زیر نمودار فشار برحسب حجم است:
$$W = S = frac { ( 2 + 3 ) times 10 ^ 5 times ( 3 – 1 ) times 10 ^ { – 3 } } { 2 } = 500 J$$
در این فرایند، حجم گاز افزایش یافته و فرایند انبساط رخ داده است. بنابراین، علامت کار منفی خواهد بود:
$$W = – 500 J$$
با داشتن تغییرات انرژی درونی و کار انجام شده، گرمای مبادله شده را بهدست میآوریم:
$$triangle U = Q + W \ W = triangle U – W = 456 – (- 500) = 956 J$$
با توجه به آنکه علامت Q مثبت است، گاز گرما گرفته است.
مسئله ۵ فصل پنجم ترمودینامیک فیزیک دهم
گازی مطابق شکل، از طریق مسیر abc از حالت a به c میرود. گاز در این مسیر، ۹۰ ژول گرما میگیرد و ۷۰ ژول کار انجام میدهد. الف) تغییر انرژی درونی گاز در مسیر abc چقدر است؟ ب) اگر برای رسیدن به حالت c فرایند از مسیر adc انجام شود، کار انجام شده توسط گاز در مقایسه با مسیر abc بیشتر است یا کمتر؟ گرمای داده شده به گاز بیشتر است یا کمتر؟ پ) اگر گاز را از مسیر خمیده از حالت c به حالت a برگردانیم، چقدر باید از آن انرژی بگیریم؟
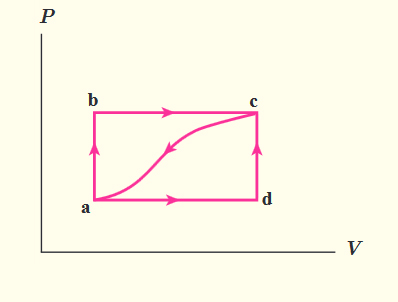
پاسخ
قسمت الف: تغییر انرژی درونی گاز در مسیر abc برابر است با:
$$triangle U = Q + W = 90 – 70 = 20 J$$
قسمت ب: کار انجام شده در نمودار فشار برحسب حجم از مساحت زیر نمودار بهدست میآید. از آنجا که مساحت زیر نمودار در مسیر adc کمتر از مسیر abc است، قدر مطلق کار نیز در این مسیر کمتر است. همچنین، نقاط ابتدا و انتهای هر دو مسیر یکسان است. بنابراین، تغییر انرژی درونی در هر دو مسیر با یکدیگر برابر است. در نتیجه، با توجه به برابر بودن تغییرات انرژی درونی در دو مسیر، گرمای دریافت شده توسط گاز در مسیر adc کمتر خواهد بود.
قسمت پ: تغییر انرژی درونی در چرخه ترمودینامیکی برابر صفر است. بنابراین، انرژی گرفته شده از گاز در مسیر c به a برابر با تغییر انرژی درونی آن در این مسیر یعنی ۲۰- ژول است.
مسئله ۶ فصل پنجم ترمودینامیک فیزیک دهم
مکعبی آلومینیومی توپری به ضلع ۲۰/۰ سانتیمتر از ۵۰/۰ درجه سلسیوس تا ۱۵۰/۰ درجه سلسیوس در فشار متعارف جو ($$1.01 times 10^ 5 Pa$$) گرم میشود. کار انجام شده توسط مکعب را محاسبه کنید.
مکعب در فشار ثابت منبسط میشود. کار انجام شده توسط آن برابر است با:
$$W = P triangle V$$
از آنجا که مکعب در فشار ثابت منبسط میشود، مقدار فشار برابر $$1.01 times 10 ^ 5 Pa $$ است. تغییرات حجم مکعب را میتوان با استفاده از رابطه $$triangle V = 3 alpha V_ 1 triangle V $$ بهدست آورد. مقدار $$alpha$$ را میتوانیم از جدول ضریب انبساط گرمایی در فصل چهارم ترمودینامیک فیزیک دهم پیدا کنیم. حجم اولیه مکعب برابر ۰/۰۰۸ مترمکعب است. با قرار دادن مقدارهای داده شده در رابطه $$triangle V = 3 alpha V_ 1 triangle V $$، تغییرات حجم مکعب پس از افزایش دما از ۵۰ به ۱۵۰ درجه سلسیوس، برابر $$5.52 times 10 ^ 5 m^ 3$$ بهدست میآید. بنابراین، مقدار کار انجام شده برابر است با:
$$W = 1.01 times 10 ^ 5 Pa times 5.52 times 10 ^ { -5 } = 5.57 J$$
به این نکته توجه داشته باشید که علامت کار منفی است
مسئله ۷ فصل پنجم ترمودینامیک فیزیک دهم
مطابق شکل زیر، حجم گازی ایدهال طی سه فرایند همفشار، همدما و بیدررو از $$V_ 1$$ به حجم بزرگتر $$V_2$$ میرسد. الف) اندازه کار انجام شده توسط گاز را در این سه فرایند مقایسه کنید. ب) دمای نهایی را در این فرایندها مقایسه کنید. پ) گرمای داده شده به گاز را در این فرایندها مقایسه کنید.
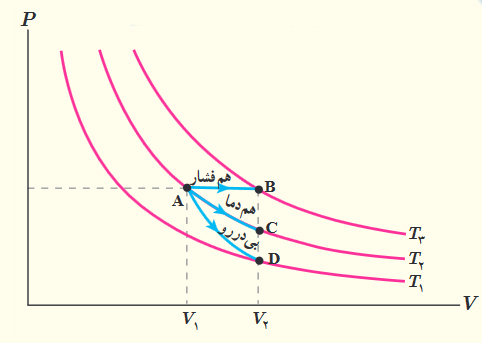
پاسخ
قسمت الف: کار انجام شده برابر مساحت زیر نمودار فشار برحسب حجم است. با توجه به نمودار بالا و مساحت زیر نمودار مربوط به هر فرایند:
کار انجام شده در فرایند همفشار > کار انجام شده در فرایند همدما > کار انجام شده در فرایند بیدررو
قسمت ب: همانطور که در نمودار رسم شده مشاهده میکنید:
$$T_3 > T_2 > T_ 1$$
در نتیجه، دمای نهایی این سه فرایند به صورت زیر با یکدیگر مقایسه میشوند:
دمای نهایی فرایند همفشار > دمای نهایی فرایند همدما > دمای نهایی فرایند بیدررو
قسمت پ: در فرایند بیدررو، مقدار گرمایی داده شده به گاز برابر صفر است. تغییرات انرژی درونی در فرایند همدما برابر صفر است. بنابراین:
$$Q = – W $$
از آنجا که کار انجام شده در فرایند انبساط، منفی است، گرما در فرایند همدما مثبت خواهد بود. مقدار گرما در فرایند همفشار با استفاده از رابطه زیر بهدست میآید:
$$Q_ {P = cte } = n C_p triangle T = frac { C_ P } { R } P triangle V = frac { C_ p } { R } | W _ { P = ctr } | $$
از آنجا که نسبت $$frac { C_ P } { R } $$ بزرگتر از یک است، گرما در فرایند همفشار بزرگتر از گرمای در فرایند همدما خواهد بود. در نتیجه داریم:
گرما در فرایند همفشار > گرما در فرایند همدما > گرما در فرایند بیدررو
پس از حل چند مسئله در مورد فرایندهای ترمودینامیکی دو مسئله در مورد مبحث چرخه ترمودینامیکی از فصل پنجم ترمودینامیک فیزیک دهم را با یکدیگر حل میکنیم. برای انجام این کار دو مسئله ۹ و ۱۲ از فصل پنجم انتخاب شده است.
مسئله ۹ فصل پنجم ترمودینامیک فیزیک دهم
شکل روبهرو چرخه طی شده توسط گازی را نشان میدهد. الف) تعیین کنید که گاز در این چرخه گرما گرفته یا از دست داده است؟ ب) اگر مقدار گرمای مبادله شده در این چرخه ۴۰۰ ژول باشد، کار انجام شده روی گاز چقدر است؟

الف: گاز از محیط گرما میگیرد، ب: ۴۰۰ ژول
الف: گاز اگرما از دست میدهد، ب: ۴۰۰ ژول
الف: گاز از محیط گرما میگیرد، ب: ۵۰۰ ژول
الف: گاز گرما از دست میدهد، ب: ۵۰۰ ژول
قسمت الف: تغییرات انرژی درونی در چرخه ترمودینامیکی برابر صفر است.
$$triangle U = Q + W = 0 \ Q = – W$$
همانطور که در تصویر بالا دیده میشود، چرخه ترمودینامیکی طی شده توسط گاز، ساعتگرد و کار انجام شده در چرخه ساعتگرد، منفی است. بنابراین، گرما مثبت خواهد بود. گرمای مثبت بدان معنا است که گاز از محیط گرما میگیرد.
قسمت ب: مقدار گرمای مبادله شده در این چرخ برابر ۴۰۰ ژول است. کار انجام شده برابر است با:
$$Q = – W \ W = – Q = -400 J = -400 J$$
مسئله ۱۲ فصل پنجم ترمودینامیک فیزیک دهم
دستگاهی متشکل از ۰/۳۲ مول گاز کامل تک اتمی حجمی برابر۲/۲ لیتر را در فشار ۲/۴ اتمسفر اشغال کرده است. این دستگاه چرخهای مطابق شکل را میپیماید که در آن فرایند CA فرایندی هم دما است. الف) دما در نقاط A و B و C چقدر است؟ ب) $$triangle U$$ را برای فرایند همدما بهدست آورید. پ) انرژی درونی نقطهها را با هم مقایسه کنید.
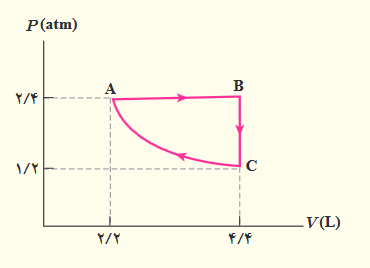
پاسخ
همانطور که در نمودار بالا دیده میشود:
- گاز طی فرایند همفشار از نقطه A به نقطه B رفته است و حجم آن از ۲/۲ لیتر به ۴/۴ لیتر افزایش یافته است.
- گاز طی فرایند همحجم از نقطه B به نقطه C رفته است و فشار آن از ۲/۴ اتمسفر به ۱/۲ اتمسفر کاهش یافته است.
- گاز طی فرایند همدما از نقطه C به نقطه A رفته است و فشار آن از ۱/۲ اتمسفر به ۲/۴ اتمسفر افزایش و حجم آن از ۴/۴ لیتر به ۲/۲ لیتر کاهش یافته است.
از آنجا که با گاز کامل سروکار داریم، باید از رابطه $$PV = nRT $$ استفاده کنیم. در این مسئله، تعداد مول گاز برابر ۰/۳۲ است. همچنین، ثابت جهانی گازها، R را تقریبا برابر $$8 frac { J } { mol . K }$$ در نظر میگیریم. دمای گاز در نقطه A به صورت زیر بهدست میآید:
$$$$P_A V_A = n R T _A $$ \ T_ A = frac { P_A V _A } { n R } \ T_ A = frac { 2.4 times 10 ^ 5 times 2.2 times 10 ^ { -3 }} { 0.32 times 8 } = 206.25 K$$
در ادامه، دمای گاز در نقطه B را بهدست میآوریم. گاز طی فرایند همفشار از نقطه A به B رفته است. بنابراین، دما در نقطه B به صورت زیر بهدست میآید:
$$frac { V _A } { T _ A } = frac { V_ B } { T _ B } \ T_ B = T_A times frac { V_B } { V _ A } \ T_ B = frac { 4.4 } { 2.2 } times 206.25 K = 2 times 206.25 K = 412 . 5 K$$
در ادامه، دمای گاز در نقطه C را بهدست میآوریم. گاز طی فرایند همحجم از نقطه B به C رفته است. بنابراین، دما در نقطه C به صورت زیر بهدست میآید:
$$frac { P _ B } { T _ B } = frac { P_ C } { T _ C } \ T_ C = T_ B times frac { P _ C } { P _ B } \ T_ C = frac { 1.2 } { 2.4 } times 412.5 K = 2 times 206.25 K = 206.25 K$$
همانطور که مشاهده میشود دمای دو نقطه A و C با یکدیگر برابر هستند. این نتیجه دور از انتظار نبود، زیرا بنا بر صورت مسئله گاز طی فرایند همدما از نقطه B به نقطه C میرود. از اینرو، دماهای این دو نقطه با یکدیگر، برابر بهدست آمدند. در قسمت ب میخواهیم تغییرات انرژی درونی گاز را طی فرایند همدما بهدست آوریم. انرژی درونی به طور مستقیم با دما تغییر میکند. در فرایند همدما، دما بدون تغییر باقی میماند. بنابراین، تغییرات انرژی درونی برابر صفر است.
در قسمت پ میخواهیم انرژی درونی سه نقطه A و B و C را با یکدیگر مقایسه کنیم. دمای دو نقطه B و C با یکدیگر برابر هستند. در نتیجه، انرژی درونی در این دو نقطه با یکدیگر برابر هستند. اما انرژی درونی نقطه C از انرژی درونی نقطههای B و C کمتر است.
در انتهای فصل پنجم ترمودینامیک فیزیک دهم در مورد ماشینهای گرمایی صحبت کردیم. در ادامه برای آشنایی بیشتر با این مبحث، دو مسئله ۱۳ و ۱۴ را با یکدیگر حل میکنیم.
مسئله ۱۳ فصل پنجم ترمودینامیک فیزیک دهم
ماشین گرمایی در هر چرخه ۱۰۰/۰ ژول گرما از منبع دمای بالا میگیرد و ۶۰/۰ ژول گرمای به منبع دما پایین میدهد و بقیه آن به کار تبدیل میشود. الف) بازده این ماشین چقدر است؟ ب) اگر هر چرخه ۰/۵۰۰ ثانیه طول بکشد، توان خروجی این ماشین چقدر است؟

الف: ۴۰ درصد، ب: ۱۰۰ وات
الف: ۵۰ درصد، ب: ۸۰ وات
الف: ۴۰ درصد، ب: ۹۰ وات
الف: ۴۰ درصد، ب: ۸۰ وات
قسمت الف: انرژی ورودی به ماشین گرمایی همان گرمای داده شده به ماشین، $$Q_H$$، و انرژی مفید خروجی، همان کار انجام شده توسط ماشین است:
$$eta = frac { | W | } { Q_H } \ eta = frac { 40 } { 100 } = 0.4 \ eta = 40 %$$
قسمت ب: توان خروجی با استفاده از رابطه زیر بهدست میآید:
$$ P = frac { | W | } { t } = frac { 40 } { 0.5 } = 80 W \ P = 80 W$$
مسئله ۱۴ فصل پنجم ترمودینامیک فیزیک دهم
ماشین گرمایی درونسوزی در هر چرخه ۸/۰۰ کیلوژول گرما از سوزاندن سوخت دریافت میکند و ۲/۰۰ کیلوزول کار تحویل میدهد. گرمای حاصل از سوخت $$5.0 times 10 ^ 4 frac { J } { g }$$ است و ماشین در هر ثانیه ۴۰/۰ چرخه را میپیماید. کمیتهای زیر را محاسبه کنید. الف) بازده ماشین، ب) سوخت مصرف شده در هر چرخه و پ) توان ماشین.
الف: ۲۵ درصد، ب: ۰/۱۶ گرم، پ: $$8.00 times 10^ 4 $$ وات
الف: ۳۵ درصد، ب: ۰/۱۶ گرم، پ: $$8.00 times 10^ 4 $$ وات
الف: ۲۵ درصد، ب: ۰/۲۰ گرم، پ: $$8.00 times 10^ 4 $$ وات
الف: ۲۵ درصد، ب: ۰/۱۶ گرم، پ: $$۶.00 times 10^ 4 $$ وات
بر طبق صورت مسئله، ماشین گرمایی درونسوز در هر چرخه ۸/۰۰ کیلوژول گرما به دلیل سوزاندن سوخت دریافت و از این مقدار ۲/۰۰ کیلوژول را به کار تبدیل میکند. بنابراین، بازده ماشین در هر چرخه برابر است با:
$$eta = frac { | W | } { Q_H } \ eta = frac { 2.00 kJ } { 8.00 kJ } = 0.25 \ eta = 25 %$$
قسمت ب: در این قسمت میخواهیم سوخت مصرف شده در هر چرخه را بهدست آوریم. گرمای حاصل از سوخت $$5.0 times 10 ^ 4 frac { J } { g }$$ به ازای هر گرم است و این ماشین در هر چرخه ۸/۰۰ کیلوزول گرما از سوزاندن سوخت دریافت میکند. بنابراین، سوخت مصرف شده در هر چرخه برابر است با:
$$frac { 8.00 times 10 ^ 3 J } { 5.0 times 10 ^ 4 J } = frac { 8 . 00 } { 50.0 } = 0.16 g$$
در نتیجه، ماشین گرمایی در هر چرخه در حدود ۰/۱۶ گرم از سوخت را مصرف میکند.
قسمت پ: توان ماشیم برابر نسبت کار به زمان انجام کار است. توان ماشین در هر ثانیه برابر است با:
$$frac { | W | } { t = 1 s } $$
ماشین در هر ثانیه، ۴۰/۰ چرخه را میپیماید و کار انجام شده در هر چرخه برابر ۲/۰۰ کیلوژول است. از اینرو، کل کار انجام شده در هر ثانیه برابر است با:
$$| W | = 40 times 2.00 times 10 ^ 3 J = 8.00 times 10 ^ 4 J $$
با محاسبه کار در هر ثانیه، توان ماشین را بهدست میآوریم:
$$P = frac { | W | } { t } = frac { 8.00 times 10 ^ 4 J } { 1 s } = 8.00 times 10 ^ 4 W$$
جمعبندی
در این مطلب از مجله فرادرس، با ترمودینامیک فیزیک دهم آشنا شدیم. در این مطلب در مورد مفاهیمی همانند دما، گرما، انتقال گرما، انبساط گرمایی، گاز کامل، قوانین گاز کامل، قانون اول و دوم ترمودینامیک و ماشین گرمایی صحبت و مسائلی را در مورد هر مبحث با یکدیگر حل کردیم.
source
